Bande de totalité
Une éclipse totale de soleil est un événement très ponctuel géographiquement et temporellement, donc exceptionnel.
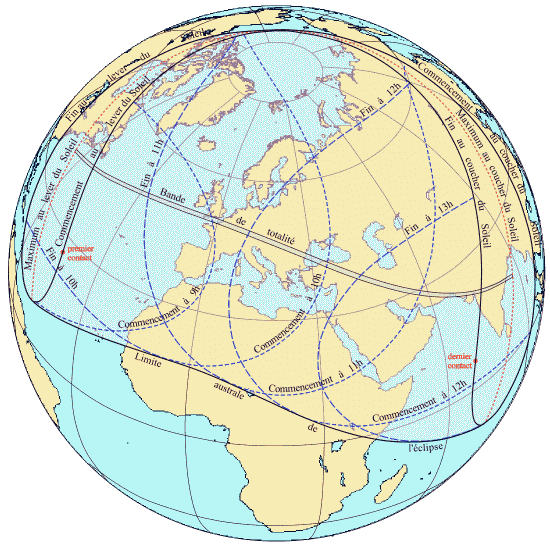
Conditions d'observation et bande de totalité de l'éclipse du 11 août 1999 (dernière éclipse totale visible en France)
Crédit :
IMCCE
Où et quand ?
La prédiction précise des éclipses est un exercice difficile, maîtrisé par un nombre restreint d'instituts dans le monde, qui relève de la métrologie du temps et de l'espace la plus poussée.
Voir les pages de l'IMCCE.
 Dis-moi comment tu tournes...
Dis-moi comment tu tournes...
Difficulté : ☆
Temps : 30
Question 1)
La durée de la rotation de la Terre est très proche de 86400 secondes (24 heures), mais sa valeur exacte est variable dans le temps. Le frottement provoqué par des effets de marées est à l'orgine d'un très lent ralentissement (de l'ordre de quelques millisecondes par siècle). Cela paraît peu, mais cumulé sur une période longue, il en resulte un décalage important.
Un des meilleurs moyens de mesurer cette variation consiste en l'étude d'observations historiques d'éclipses. Le décalage temporel (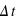 ) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
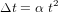 .
Ici,
.
Ici,  est la date de l'événement (compté en siècles avant 1820), et
est la date de l'événement (compté en siècles avant 1820), et  est mesuré en s par siecle2.
est mesuré en s par siecle2.
Un texte babylonien conservé au British Museum à Londres décrit une éclipse solaire totale, observée à Babylone le 15 avril de l'an 136 avant notre ère. En comparant l'heure de début et de fin décrits dans ce texte à un calcul des positions de la Terre et du Soleil, on trouve pour
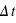 une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante
une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante 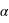 ainsi que son incertitude!
ainsi que son incertitude!
[
points]
136+1820-1 ans = 20 siècles
Question 2)
Un autre texte décrit une observation d'une éclipse totale, en Mésopotamie, il y a 40 siècles. A priori, l'observation état plus ancienne ( plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de
plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de 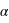 et du coup de mieux caractériser la rotation de la Terre.
et du coup de mieux caractériser la rotation de la Terre.
Le problème est que, dans ce cas, le texte ne mentionne pas le lieu d'observation. L'incertitude spatiale est de l'ordre de 1000 km le long de la bande de totalité, quasiment parallèle au parallèle de latitude 35 deg. Traduire l'incertitude spatiale en incertitude temporelle. Calculez aussi l'incertitude sur 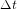 qui résulte de l'incertitude sur
qui résulte de l'incertitude sur  calculée à l'exercice précédent (1 s/siècle2).
calculée à l'exercice précédent (1 s/siècle2).
Calculer la longueur du parallèle 35 deg.
Question 3)
La date précise de l'éclipse est connue, par la mécanique céleste, plus précisement que la rotation de la Terre.
Cette éclipse permet-elle de préciser la rotation de la Terre ?
- Question 1
Aide :
136+1820-1 ans = 20 siècles
Solution :
Pour 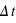 =11200 s, on trouve
=11200 s, on trouve  =28 s/siecle2.
Pour
=28 s/siecle2.
Pour 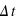 =12150 s, on trouve
=12150 s, on trouve  =30 s/siecle2.
Résultat:
=30 s/siecle2.
Résultat: 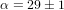 s/siecle2.
s/siecle2.
- Question 2
Aide :
Calculer la longueur du parallèle 35 deg.
Solution :
Incertitude de localisation : L'équateur mesurant 40 000 km, le parallèle à 35 deg mesure lui 32 700 km.
Une bande de longueur 1000 km est parcourue par la rotation de la Terre en
24 / 32.7 = 0.73 h, soit 44 min.
Incertitude de la rotation de la Terre : 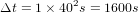 . Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
. Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
- Question 3
Solution :
La comparaison des 2 résultats précédents montre que
l'incertitude sur la localisation géographique, supérieure à l'incertitude temporelle sur la rotation de la Terre, ne permet pas de situer la Terre précisément par rapport à l'éclipse.

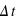 ) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
) du moment précis d'une éclipse dû au ralentissement de la rotation de la Terre peut atteindre plusieurs heures! On trouve la relation mathématique suivante :
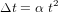 .
Ici,
.
Ici,  est la date de l'événement (compté en siècles avant 1820), et
est la date de l'événement (compté en siècles avant 1820), et  est mesuré en s par siecle2.
est mesuré en s par siecle2.
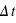 une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante
une valeur entre 11200 et 12150 secondes. Déduisez-en la valeur de la constante 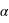 ainsi que son incertitude!
ainsi que son incertitude!
 plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de
plus élevé), on pourrait espérer avoir une mesure plus précise de la valeur de 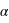 et du coup de mieux caractériser la rotation de la Terre.
et du coup de mieux caractériser la rotation de la Terre.
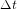 qui résulte de l'incertitude sur
qui résulte de l'incertitude sur  calculée à l'exercice précédent (1 s/siècle2).
calculée à l'exercice précédent (1 s/siècle2).
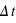 =11200 s, on trouve
=11200 s, on trouve  =28 s/siecle2.
Pour
=28 s/siecle2.
Pour 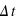 =12150 s, on trouve
=12150 s, on trouve  =30 s/siecle2.
Résultat:
=30 s/siecle2.
Résultat: 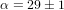 s/siecle2.
s/siecle2.
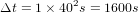 . Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).
. Au bout de 40 siècles, l'incertitude est de l'ordre de 1600 s (un peu moins d'une demi-heure).