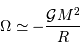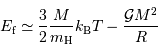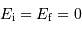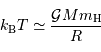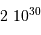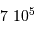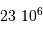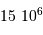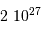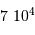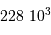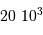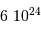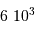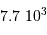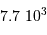IC1396 en infrarouge

Nuage interstellaire (dans la nébuleuse IC1396), d'apparence bien développée dans le proche infrarouge, hébergeant de nombreuses étoiles en formation. L'aspect filamentaire provient des effets d'érosion du vent stellaire d'une étoile massive (hors champ, sur la gauche du cliché).
Crédit :
NASA/Spitzer
IC1396 en lumière visible

Même région qu'à la
figure
précédente, mais en lumière visible et non infrarouge.
On y distingue les résidus du nuage interstellaire ayant conduit à
une genèse stellaire. En effet, en lumière visible, les régions
les plus denses du nuage apparaissent totalement obscures, ou
réfléchissant le rayonnement intense des étoiles jeunes
nouvellement formées.
Crédit :
NASA/Spitzer
Contraste
Le milieu interstellaire montre des régions de matière très froide (typiquement 10 K) et très peu dense (quelques particules 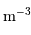 ), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement
), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement 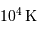 en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement
en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement 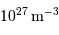 ).
).
Comble du contraste : les étoiles jeunes se situent au sein de ces régions, ou ce qu'il en reste dès lors que le rayonnement de l'étoile parvient à percer.
Etat initial
On suppose le nuage initialement très peu dense et très froid. Il ne possède ni énergie cinétique (il est trop froid), ni énergie potentielle d'interaction (la matière est beaucoup trop diluée). On résume la situation par une énergie mécanique totale quasi nulle (plus précisément : ces énergies sont initialement totalement négligeables par rapport aux énergies cinétiques et potentielles à venir) :
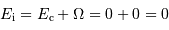
Etat final
Dans un état condensé, l'énergie cinétique qui relate l'agitation thermique n'est plus négligeable. Si 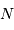 atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de
atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de 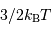 par nucléon :
par nucléon :
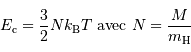
L'énergie potentielle rend compte de la très énergique interaction gravitationnelle des 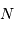 atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours
atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours 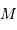 la masse concernée, et
la masse concernée, et 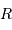 le rayon final de l'objet condensé.
le rayon final de l'objet condensé.
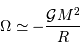
L'énergie totale s'exprime alors :
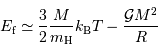
Effondrement et échauffement
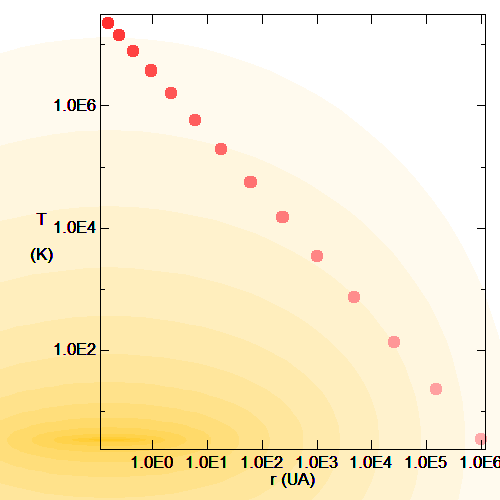
Lorsque le nuage se contracte, il se réchauffe.
Crédit :
ASM
Et la rotation ?
La conservation du moment cinétique et les collisions entre particules conduit à aplatir le système. En effet, par suite des collisions, les composantes de vitesse parallèles au moment cinétique vont peu à peu s'annuler, en gardant une valeur moyenne nulle, quand les vitesses perpendiculaires se thermalisent. Ceci est traité plus en détail à la page consacrée aux disques d'accrétion.


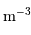 ), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement
), qui contrastent singulièrement avec les étoiles, objets chauds (typiquement 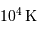 en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement
en surface, et plusieurs millions de degrés à l'intérieur) et dense (densité particulaire de typiquement 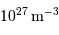 ).
).
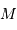 de gaz conduisant à un corps condensé de rayon
de gaz conduisant à un corps condensé de rayon 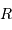 donne une température centrale variant comme
donne une température centrale variant comme 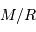 , d'autant plus élevée que le corps est massif et dense.
, d'autant plus élevée que le corps est massif et dense.
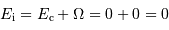
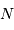 atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de
atomes d'hydrogène sont concernés, l'énergie cinétique (thermique) vaut, à compter de 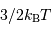 par nucléon :
par nucléon :
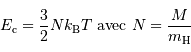
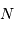 atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours
atomes rassemblés. Cette énergie est négative, car l'interaction gravitationnelle est attractive. On se contente d'un ordre de grandeur, donné par l'analyse dimensionnelle, avec toujours 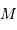 la masse concernée, et
la masse concernée, et 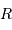 le rayon final de l'objet condensé.
le rayon final de l'objet condensé.