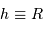 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
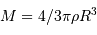 conduisent à :
conduisent à :
L'égalité dans le cas limite, 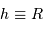 , et la définition de la masse pour une masse volumique uniforme
, et la définition de la masse pour une masse volumique uniforme
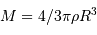 conduisent à :
conduisent à :
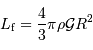
soit
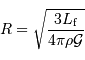
AN : 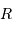 de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.
de l'ordre de 550 km. Avec une taille inférieure, un objet sera patatoïdal ; au-delà, il tend vers une forme sphérique.