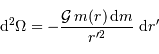
De l'expression du travail élémentaire qui précède, on tire l'expression de la variation d'énergie potentielle d'interaction gravitationnelle sur une étape élémentaire :
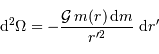
Avec 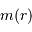 la masse accrétée au rayon
la masse accrétée au rayon 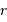 et
et 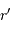 une position entre
une position entre 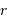 et
et 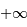 . Une première étape d'intégration conduit à apporter la masse
. Une première étape d'intégration conduit à apporter la masse 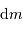 de l'infini à la surface :
de l'infini à la surface :
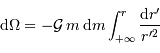
Le calcul de l'intégrale donne ![\left[ - \displaystyle{1\over r'}\right]_\infty^r = - \displaystyle{1\over r}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation46.png) . D'où la variation de potentiel :
. D'où la variation de potentiel :
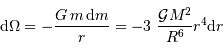
après avoir remplacé 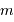 et
et 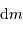 par leur valeurs.
Et donc finalement :
par leur valeurs.
Et donc finalement :
![\Omega = \int_0^R {\mathrm{d}} \Omega = \left[ - 3 { {\cal G} M^2\over R^6} {r^5\over 5} \right]_0^R = -{3\over 5} { {\cal G} M^2\over R}](../pages_physique-evolution/equations_energie-potentielle-gravitationnelle/equation50.png)
On retrouve ce résultat classique. L'expression est homogène ; le signe négatif rappelle que la formation d'une concentration de matière a dégagé de l'énergie (ou qu'il faut en dépenser pour démonter l'objet).