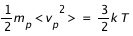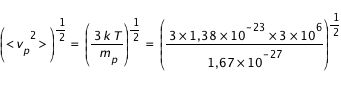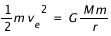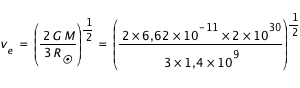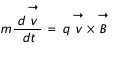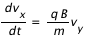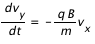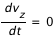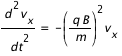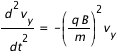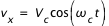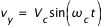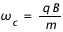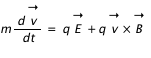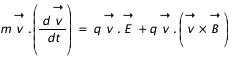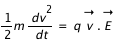Problèmes de physique appliqués au Soleil
- Introduction
- L'énergie émise par le Soleil
- Introduction
- L'énergie provenant du Soleil
- L'intérieur du Soleil
- L'équilibre hydrostatique local de l'intérieur
- L'équilibre hydrostatique global
- Source de l'énergie solaire
- Température du centre du Soleil
- Le vent solaire
- L'équilibre thermodynamique de la couronne
- Trajectoire des particules
- Trajectoire des particules
- Accélération des particules
- Accélération des particules
Introduction
 Introduction
Introduction
Ce chapitre est une présentation de quelques problèmes de physique sous forme de cours ou d'exercices appliqués au Soleil. Ce chapitre est d'une difficulté plus soutenue, et nécessite une certaine familiarité avec les équations.
L'énergie émise par le Soleil
Introduction
 Introduction
Introduction
Le Soleil émet du rayonnement, donc de l'énergie, dans toute les directions de l'espace. En mesurant l'énergie du rayonnement reçu au niveau de la Terre, on peut remonter à l'énergie totale émise par le Soleil. La puissance émanant du Soleil et reçue au niveau de la Terre est la constante solaire.
L'énergie provenant du Soleil
Auteur: Arnaud Beck
 Energie émise par le Soleil
Energie émise par le Soleil
Difficulté : ☆☆
Temps : 10 minutes
Question 1)
Sachant que la puissance provenant du Soleil reçue par la Terre au niveau des nuages est de 1360 W m-2 (la fameuse "constante solaire"), et sachant que le Soleil est à 150 millions de km de la Terre, en déduire la puissance rayonnée par le Soleil.
Le rayonnement solaire se propage suivant une sphère, dans toutes les directions. Plus le rayon de cette sphère augmente, plus le rayonnement par unité de surface de cette sphère diminue. Rappelons que la surface d'une sphère est 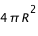 .
.
L'intérieur du Soleil
Auteur: Arnaud Beck
L'équilibre hydrostatique local de l'intérieur
Supposons que le Soleil soit tout simplement une boule de gaz à l'équilibre hydrostatique. C'est-à-dire que le Soleil est une boule de rayon 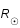 , au repos, et dont la température T , la densité ρ et la pression P ne dépendent que du rayon r où l'on se place.
, au repos, et dont la température T , la densité ρ et la pression P ne dépendent que du rayon r où l'on se place.
Étudions un élément infinitésimal cylindrique de cette boule. Cet élément, situé à une distance r du centre du Soleil, est de section ds et de hauteur dr. Sa densité est celle du milieu environnant, ρ(r), et sa masse vaut dm = ρ(r) dr ds (voir figure ci dessous) :
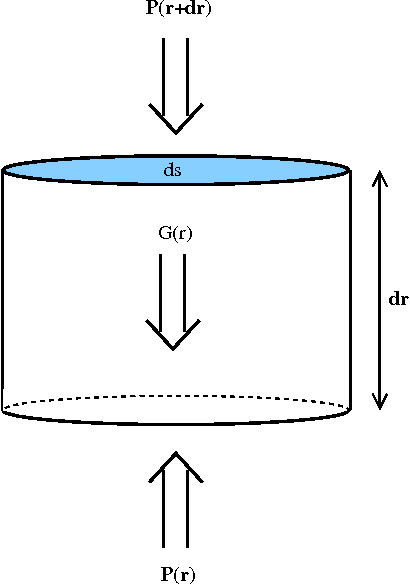
Crédit :
Arnaud Beck, LESIA
Trois forces s'exercent sur ce cylindre de gaz. Deux forces de pression P(r)ds et P(r+dr)ds ainsi que le poids du cylindre :
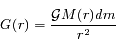
où 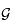 est la constante universelle de gravitation et M(r) est la masse totale contenue dans la sphère de rayon r, soit :
est la constante universelle de gravitation et M(r) est la masse totale contenue dans la sphère de rayon r, soit :
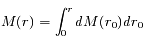
avec
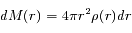
Supposer que le Soleil est au repos implique que la somme des forces s'exerçant sur ce cylindre est nulle. C'est-à-dire que la différence entre les forces de pression est exactement équilibrée par la force de gravité. On a donc l'équation d'équilibre hydrostatique locale :
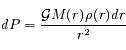
L'équilibre hydrostatique global
Pour obtenir une équation globale, multiplions chaque membre de l'équation par le volume
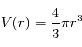
et intégrons le résultat entre r=0 et r= 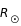 .
.
Le membre de droite donne :
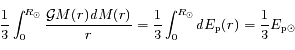
Où Ep est l'énergie potentielle gravitationnelle et 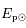 l'énergie potentielle gravitationnelle totale du Soleil.
l'énergie potentielle gravitationnelle totale du Soleil.
Le membre de gauche donne :
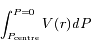
où Pcentre est la pression au centre du Soleil et en supposant que la pression est nulle à sa surface. Une intégration par partie donne :
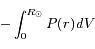
En faisant l'hypothèse des gaz parfaits on a : PV=NkBT où N est le nombre totale de particules dans le système et kB la constante de Boltzman. En remarquant que l'énergie interne du système s'écrit 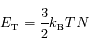 , on peut récrire l'équation des gaz parfaits en :
, on peut récrire l'équation des gaz parfaits en :
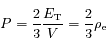
où ρe est la densité volumique d'énergie interne. En la réinjectant dans l'équation précédente le membre de gauche donne finalement :
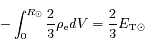
où 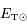 est l'énergie interne totale du Soleil. Au final, l'équation d'équilibre hydrostatique intégrée donne donc :
est l'énergie interne totale du Soleil. Au final, l'équation d'équilibre hydrostatique intégrée donne donc :
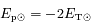 .
.
Cela signifie que si le Soleil se contracte et que son énergie potentielle diminue de ΔEp, son énergie thermique augmente de ΔET=ΔEp/2 et le Soleil se réchauffe. Pendant une contraction, la moitié de l'énergie potentielle gravitationnelle en jeu est donc convertie en énergie interne. L'autre moitié est en fait évacuée sous forme de rayonnement.
Source de l'énergie solaire
Auteur: Arnaud Beck
 La gravité est elle la source de l'énergie solaire ?
La gravité est elle la source de l'énergie solaire ?
Difficulté : ☆
Temps : 5 minutes
Question 1)
On a vu que le rayonnement solaire peut être alimenté par la contraction du Soleil. Sachant que le Soleil est vieux de plus de 4 milliards d'année, que sa masse vaut 2.1030 kg, son rayon 7.108 m, la constante de gravitation 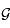 =6,7.10-11 m3 kg-1 s-2 et connaissant la puissance rayonnée par le Soleil (d'après l'exercice précédent ), cette hypothèse est-elle réaliste ?
=6,7.10-11 m3 kg-1 s-2 et connaissant la puissance rayonnée par le Soleil (d'après l'exercice précédent ), cette hypothèse est-elle réaliste ?
On pourra supposer que le Soleil est de densité homogène car cela ne modifie pas de manière significative son énergie potentielle gravitationnelle totale.
Température du centre du Soleil
Auteur: Arnaud Beck
 Calcul de la température
Calcul de la température
Difficulté : ☆☆
Temps : 10 min
Question 1)
En conservant les hypothèses mentionnées ci-dessus et en supposant de plus que le Soleil est de densité homogène et uniquement composé d'hydrogène dont un atome pèse μ=1,6.10-27 kg, en déduire la température approximative du milieu de l'intérieur solaire.
A partir de l'équation d'équilibre hydrostatique local, on peut appliquer la loi des gaz parfaits en supposant la densité constante et en déduire la température.
Le vent solaire
L'équilibre thermodynamique de la couronne
Faisons maintenant l'hypothèse absurde que la couronne solaire est à l'équilibre thermodynamique. Cela se traduit par l'égalité entre l'énergie thermique et l'énergie cinétique des particules du milieu, ce que l'on peut écrire :
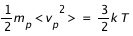
où mp et <vp2> sont respectivement la masse et la vitesse quadratique moyenne d'un proton dans la région considérée, k la constante de Boltzmann et T la température du milieu.
Si l'on se place dans la couronne, à une distance de 3 rayons solaires, où la température est estimée à 3 millions de Kelvin, on peut en déduire <vp> :
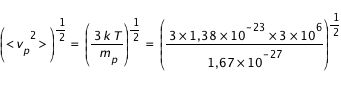
On trouve donc <vp2>1/2 ≈ 2,7 105 m.s-1.
Calculons maintenant la vitesse d'évasion, grâce à l'équation :
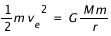
Ce qui permet d'en déduire la vitesse d'évasion :
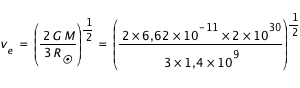
On trouve donc une vitesse d'évasion de 2,5 105 m.s-1. Légèrement inférieure à la vitesse thermique des protons du milieu. Cela signifie donc qu'une grande partie des particules s'échappe alors de l'attraction solaire, formant ainsi le vent solaire.
Trajectoire des particules
Trajectoire des particules
L'atmosphère du Soleil étant magnétisé, il est intéressant d'étudier la trajectoire des particules chargées en présence d'un champ magnétique. Nous considérons un champ magnétique uniforme dirigé suivant l'axe z. Nous considérons une particule dont les composantes de la vitesse sont suivant x et y. L'équation fondamentale de la dynamique décrivant le mouvement d'une particule chargée dans un champ magnétique s'écrit :
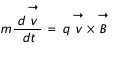
Les quantité v et B sont vectorielles. En projetant cette équation, on obtient les équations suivantes :
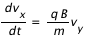
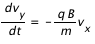
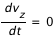
Soit:
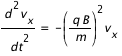
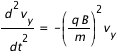
En tenant compte des conditions initiales différentes pour la composante x et y, on trouve :
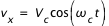
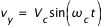
Les composantes de la vitesse de la particule oscillent entre -Vc et +Vc à la fréquence de Larmor définit par :
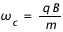
Ces équations définissent donc une rotation de la particule dans le plan (Oxy) perpendiculaire à la direction du champ magnétique. Autrement dit, une particule se propage dans le champ magnétique suivant un mouvement de rotation dans un plan perpendiculaire à la direction du champ magnétique. Une particule accélérée se propage donc dans l'atmosphère solaire en suivant les lignes de champ magnétique. De même, les particules chargées émises par le Soleil se propagent dans l'espace interplanétaire en suivant les lignes de champ magnétique.
Trajectoire d'une particule chargée dans un champ magnétique
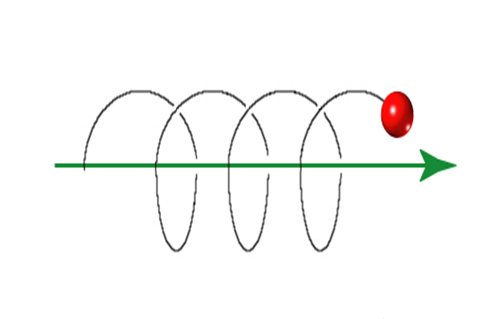
Trajectoire d'une particule chargée dans un champ magnétique.
Crédit :
Cyril Dauphin - Observatoire de Paris, LUTh
Accélération des particules
Accélération des particules
L'équation de la dynamique des particules chargées dans un champ électrique et magnétique s'écri t:
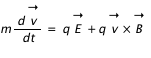
v, E et B sont des quantités vectorielles. En multipliant à droite et à gauche par v, on obtient :
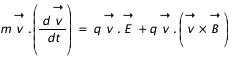
Soit:
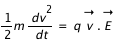
L'énergie cinétique vaut 1/2 mv2. La variation d'énergie de la particule est donc uniquement due au travail du champ électrique. Étudier l'accélération des particules lors des éruptions solaires revient donc à comprendre l'apparition et le développement de champs électriques intenses dans l'atmosphère solaire. La théorie physique décrivant le couplage du plasma avec le champ magnétique prédit un développement turbulent du champ électrique aux petites échelles spatiales lors d'une éruption solaire.
Réponses aux exercices
pages_physique-solaire/so-energie.html
Exercice
'Energie émise par le Soleil'
- Question 1
Aide :
Le rayonnement solaire se propage suivant une sphère, dans toutes les directions. Plus le rayon de cette sphère augmente, plus le rayonnement par unité de surface de cette sphère diminue. Rappelons que la surface d'une sphère est 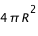 .
.
pages_physique-solaire/so-exo-energie-solaire.html
Exercice
'La gravité est elle la source de l'énergie solaire ?'
pages_physique-solaire/so-exo-hydrostatique.html
Exercice
'Calcul de la température'
 Introduction
Introduction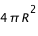 .
.
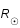 , au repos, et dont la température T , la densité
, au repos, et dont la température T , la densité 
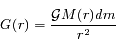
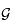 est la constante universelle de gravitation et M(r) est la masse totale contenue dans la sphère de rayon r, soit :
est la constante universelle de gravitation et M(r) est la masse totale contenue dans la sphère de rayon r, soit :
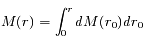
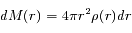
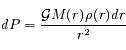
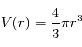
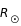 .
.
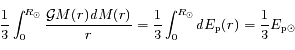
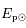 l'énergie potentielle gravitationnelle totale du Soleil.
l'énergie potentielle gravitationnelle totale du Soleil.
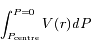
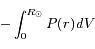
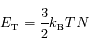 , on peut récrire l'équation des gaz parfaits en :
, on peut récrire l'équation des gaz parfaits en :
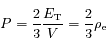
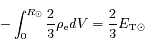
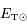 est l'énergie interne totale du Soleil. Au final, l'équation d'équilibre hydrostatique intégrée donne donc :
est l'énergie interne totale du Soleil. Au final, l'équation d'équilibre hydrostatique intégrée donne donc :
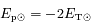 .
.
 =6,7.10-11 m3 kg-1 s-2 et connaissant la puissance rayonnée par le Soleil (d'après
=6,7.10-11 m3 kg-1 s-2 et connaissant la puissance rayonnée par le Soleil (d'après