Faisons maintenant l'hypothèse absurde que la couronne solaire est à l'équilibre thermodynamique. Cela se traduit par l'égalité entre l'énergie thermique et l'énergie cinétique des particules du milieu, ce que l'on peut écrire :

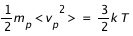
où m_p et <v_p²> sont respectivement la masse et la vitesse quadratique moyenne d'un proton dans la région considérée, k la constante de Boltzmann et T la température du milieu.

Si l'on se place dans la couronne, à une distance de 3 rayons solaires, où la température est estimée à 3 millions de Kelvin, on peut en déduire <v_p> :

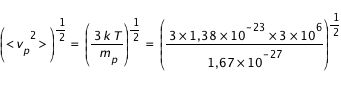
On trouve donc <v_p²>^1/2 ≈ 2,7 10⁵ m.s^-1.

Calculons maintenant la vitesse d'évasion, grâce à l'équation :

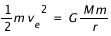
Ce qui permet d'en déduire la vitesse d'évasion :

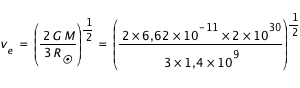
On trouve donc une vitesse d'évasion de 2,5 10⁵ m.s^-1. Légèrement inférieure à la vitesse thermique des protons du milieu. Cela signifie donc qu'une grande partie des particules s'échappe alors de l'attraction solaire, formant ainsi le vent solaire.