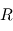 le rayon de l'anneau et
le rayon de l'anneau et 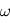 sa vitesse de rotation. On impose un gravité artificielle, c'est-à-dire une force centrifuge égale à
sa vitesse de rotation. On impose un gravité artificielle, c'est-à-dire une force centrifuge égale à 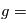 9.81
9.81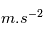 . On a donc la relation
. On a donc la relation 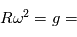 9.81
9.81 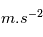 .
.
Soit 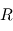 le rayon de l'anneau et
le rayon de l'anneau et 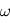 sa vitesse de rotation. On impose un gravité artificielle, c'est-à-dire une force centrifuge égale à
sa vitesse de rotation. On impose un gravité artificielle, c'est-à-dire une force centrifuge égale à 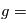 9.81
9.81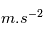 . On a donc la relation
. On a donc la relation 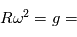 9.81
9.81 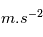 .
.
Supposons que la vitesse maximale des astronautes dans l'anneau soit atteinte lorsqu'ils courent le long de l'anneau. Cette vitesse est perpendiculaire à l'axe de rotaion, et dirigée vers le bas ou vers le haut relativement à l'astronaute, c'est à dire qu'elle s'ajoute ou se soustrait à son poids. Un champion olympique peut atteindre 10 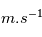 , on supposera ici que la vitesse maximale que peut atteindre un astronaute dans l'anneau est moitié moindre soit
, on supposera ici que la vitesse maximale que peut atteindre un astronaute dans l'anneau est moitié moindre soit  5
5 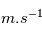 . On impose également que son poids ne doit pas varier de plus de 20 % lorsqu'il se déplace (imaginez courir et un cinquième de votre poids se rajoute à vous : c'est désagréable mais encore supportable).
. On impose également que son poids ne doit pas varier de plus de 20 % lorsqu'il se déplace (imaginez courir et un cinquième de votre poids se rajoute à vous : c'est désagréable mais encore supportable).
On obtient donc une magnitude de la force de Coriolis maximale de 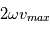 . Avec un critère de 10 % de variation du poids, on obtient la relation
. Avec un critère de 10 % de variation du poids, on obtient la relation 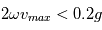
En utilisant 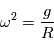 , on obtient
, on obtient 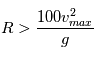 , soit un rayon minimal de 254 m.
, soit un rayon minimal de 254 m.