Auteur: EM
 Modèle simplifié d'une tornade
Modèle simplifié d'une tornade
Difficulté : ☆☆☆
Temps : 1 h
On modélise une tornade par une circulation tangentielle 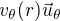 autour d'un centre. Le rayon caractéristique de la tornade est défini par
autour d'un centre. Le rayon caractéristique de la tornade est défini par 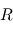 tel que : pour
tel que : pour 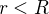 ,
, 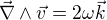 et pour
et pour 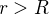 ,
, 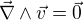 .
.
Question 2)
En pratique, 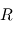 est inférieur au kilomètre et
est inférieur au kilomètre et 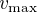 de l'ordre de 100 m/s. Quelle approximation est la plus justifiée : cyclostrophique ou géostrophique ?
de l'ordre de 100 m/s. Quelle approximation est la plus justifiée : cyclostrophique ou géostrophique ?
[1 points]
Calculer le nombre de Rossby 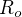 et conclure.
et conclure.
La latitude du lieu étant inconnue, donner un encadrement de 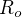 .
.
Question 3)
Exprimer alors une équation différentielle portant sur la pression 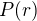 . On considèrera par la suite que
. On considèrera par la suite que 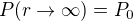 .
.
[2 points]
Utiliser l'équation de Navier-Stokes simplifée pour le cas cyclostrophique.
L'approximation cyclostrophique équilibre le gradient de pression avec la force d'inertie (centrifuge ici).
Auteur: EM
 Estimation de la circulation dans une dépression.
Estimation de la circulation dans une dépression.
Difficulté : ☆☆
Temps : 30 min
On considère une dépression martienne de rayon 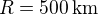 et de différence de pression en son centre avec la pression moyenne à la surface de Mars
et de différence de pression en son centre avec la pression moyenne à la surface de Mars 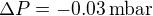 . Cette dépression se situe à la latitude
. Cette dépression se situe à la latitude  . On se placera par la suite dans le cadre de l'approximation géostrophique. La température moyenne sur Mars est voisine de
. On se placera par la suite dans le cadre de l'approximation géostrophique. La température moyenne sur Mars est voisine de 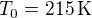 , la pression moyenne de surface voisine de
, la pression moyenne de surface voisine de 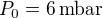 , l'accélération de la gravité y vaut
, l'accélération de la gravité y vaut 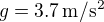 et la masse molaire de l'atmosphère y est de
et la masse molaire de l'atmosphère y est de 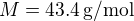 .
.
Question 1)
Calculer la masse volumique 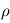 de l'atmosphère à la surface de Mars.
de l'atmosphère à la surface de Mars.
[1 points]
Utiliser la loi des gaz parfaits.
Question 2)
Calculer la valeur du paramètre de Coriolis 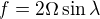 .
.
[1 points]
La durée du jour sidéral martien est de 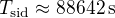 .
.
Question 3)
Estimer l'ordre de grandeur du gradient radial de pression dans cette dépression.
[1 points]
Comme on raisonne en ordre de grandeur, on peut estimer ce gradient comme la différence de pression divisée par la distance radiale caractéristique.
Question 4)
En appliquant la relation géostrophique, estimer la norme 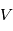 de la vitesse du vent tangentiel à la distance
de la vitesse du vent tangentiel à la distance 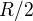 du centre de la dépression. Quelle sera sa direction ?
du centre de la dépression. Quelle sera sa direction ?
[2 points]
Appliquer la relation du cours définissant l'approximation géostrophique, à savoir l'équilibre entre le gradient de pression et la force de Coriolis.
Pour le sens de rotation, le raisonnement est identique au cas terrestre.
Question 5)
Vérifier a posteriori la validité de l'approximation géostrophique.
[1 points]
Calculer le nombre de Rossby 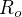 pour répondre à la question demandée.
pour répondre à la question demandée.
Question 6)
Les frottements à la surface entraînent une déviation du vent à proximité d'un angle valant 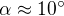 par rapport aux isobares (considérés ici comme des cercles concentriques). Exprimer le flux de masse gazeuse entrant par la surface latérale de la dépression, de périmètre
par rapport aux isobares (considérés ici comme des cercles concentriques). Exprimer le flux de masse gazeuse entrant par la surface latérale de la dépression, de périmètre 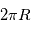 et s'étendant verticalement sur une échelle de hauteur
et s'étendant verticalement sur une échelle de hauteur 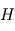 . En déduire alors la vitesse moyenne verticale du vent au sein de la dépression et son signe (ascendant ou descendant).
. En déduire alors la vitesse moyenne verticale du vent au sein de la dépression et son signe (ascendant ou descendant).
[2 points]
Attention : le vent vertical se déduit de la conservation de la masse au sein de la dépression !
Auteur: EM
 Courant jet sur Terre
Courant jet sur Terre
Difficulté : ☆☆☆
Temps : 1 h
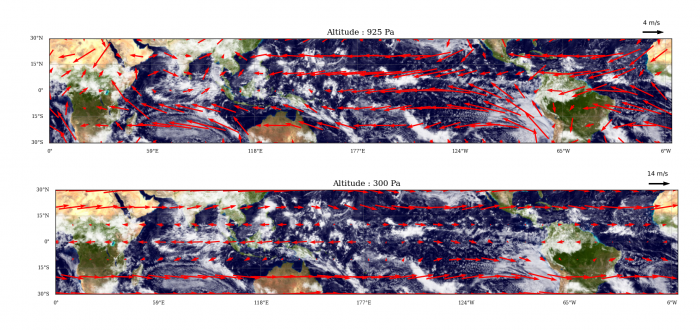
On considère les températures moyennées (zonalement, c'est-à-dire en longitude) au niveau de la surface pour les mois de janvier (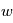 ) et juillet (
) et juillet (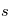 ) à différentes latitudes sur Terre.
) à différentes latitudes sur Terre.
Moyenne zonale des températures
| Latitude | 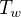 [°C] [°C] | 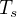 [°C] [°C] |
|---|
| 30°N | +12 | 25 |
| 45°N | 0 | 20 |
| 60°N | -12 | 15 |
Question 1)
Estimer le gradient de température sur la direction nord-sud à 45°N en janvier et en juillet. On donne le rayon terrestre 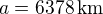 .
.
[2 points]
Il pourra être utile de connaître la distance sous-tendue par un degré d'angle dans la direction d'un méridien.
Question 4)
L'équation obtenue précédemment se généralise sous la forme 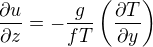 et s'appelle équation du vent thermique. Calculer le cisaillement vertical du vent zonal
et s'appelle équation du vent thermique. Calculer le cisaillement vertical du vent zonal 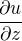 en utilisant cette équation. On donne la vitesse angulaire de la rotation sidérale terrestre
en utilisant cette équation. On donne la vitesse angulaire de la rotation sidérale terrestre 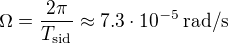 .
.
[1 points]
Appliquer la formule précédemment obtenue.
Question 5)
En considérant le vent nul à la surface et la température constante avec l'altitude, estimer alors la vitesse du vent zonal au sommet de la troposphère à une altitude 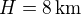 (soit environ une échelle de hauteur) en hiver puis en été. Dans quelle direction souffle ce vent (appelé courant jet) ?
(soit environ une échelle de hauteur) en hiver puis en été. Dans quelle direction souffle ce vent (appelé courant jet) ?
[2 points]
Intégrer verticalement l'équation précedente.
- Question 1
Solution :
L'énergie reçue en haut de l'atmosphère reste la même, avec ou sans atmopshère. Il n'y a pas d'atmosphère pour transporter un excès d'énergie, la conservation de l'énergie s'applique donc au niveau local : les deux courbes se superposent.
- Question 2
Solution :
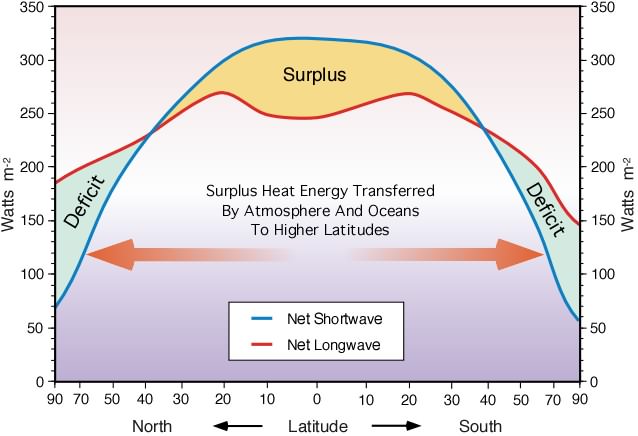
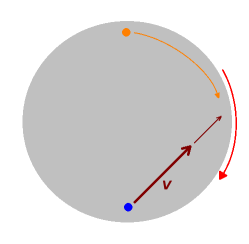
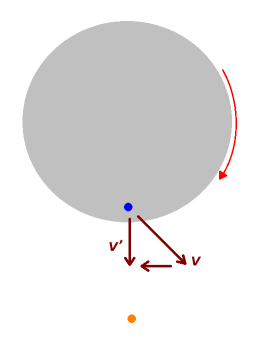
La réponse est résumée dans le schéma suivant.
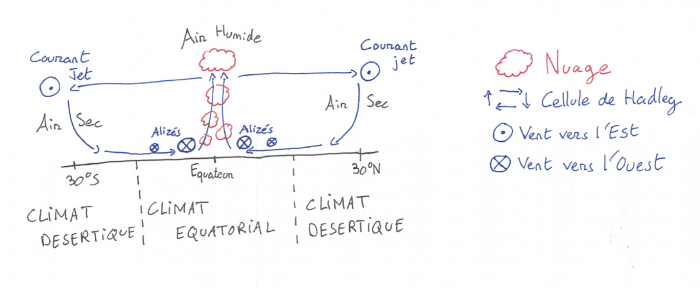
Crédit :
Thomas Navarro
Remarquons tout de même l'influence des continents et des océans sur cette circulation. Même en en tenant compte, la réalité s'avère beaucoup plus complexe que cette explication simple quoique juste, car il faut tenir des variations saisonnières et interannuelles, de la circulation océanique, de modes propres de l'atmosphère, etc ...
- Question 3
Solution :
Voir cours.
Si la vitesse est nulle, la dérivée lagrangienne est égale à la dérivée eulérienne. En effet, s'il n'y a pas de mouvement du fluide, suivre la particule ou rester en point fixé revient au même.
- Question 4
Aide :
Un vortex de lavabo est-il un système géostrophique, cyclostrophique ou aucun des deux ?
Solution :
Le nombre de Rossby associé à l'écoulement dans un lavabo avec les ordres de grandeurs habituels est très grand devant 1. L'écoulement y est donc cyclostrophique, sans influence mesurable de la force de Coriolis et donc sans dépendance avec l'hémisphère où le lavabo se trouve.
Il n'en reste pas moins votre ami. Aimez-le malgré tout.
 Modèle simplifié d'une tornade
Modèle simplifié d'une tornade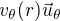 autour d'un centre. Le rayon caractéristique de la tornade est défini par
autour d'un centre. Le rayon caractéristique de la tornade est défini par 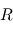 tel que : pour
tel que : pour 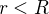 ,
, 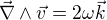 et pour
et pour 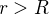 ,
, 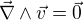 .
.
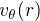 en tout point de l'espace. Exprimer en particulier la vitesse maximale
en tout point de l'espace. Exprimer en particulier la vitesse maximale 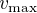 en fonction de
en fonction de 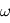 et de
et de 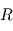 . Où est-elle atteinte ?
. Où est-elle atteinte ?
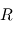 est inférieur au kilomètre et
est inférieur au kilomètre et 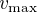 de l'ordre de 100 m/s. Quelle approximation est la plus justifiée : cyclostrophique ou géostrophique ?
de l'ordre de 100 m/s. Quelle approximation est la plus justifiée : cyclostrophique ou géostrophique ?
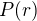 . On considèrera par la suite que
. On considèrera par la suite que 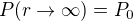 .
.
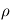 de l'atmosphère constante. Intégrer alors cette équation différentielle et exprimer
de l'atmosphère constante. Intégrer alors cette équation différentielle et exprimer 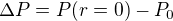 en fonction de
en fonction de 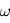 ,
, 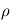 et
et 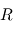 , puis de
, puis de 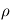 et
et 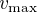 . Justifier le signe de
. Justifier le signe de 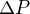 .
.
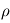 à la surface pour la Terre et pour Mars à l'aide de la loi des gaz parfaits. À l'aide des données du cours, calculer alors
à la surface pour la Terre et pour Mars à l'aide de la loi des gaz parfaits. À l'aide des données du cours, calculer alors 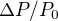 pour une tornade terrestre avec
pour une tornade terrestre avec 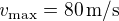 . En supposant la même valeur de
. En supposant la même valeur de 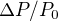 sur Mars, estimer alors
sur Mars, estimer alors 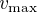 sur Mars.
sur Mars.
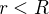 ou
ou 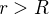 .
.
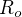 et conclure.
et conclure.
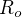 .
.
 à
à 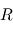 , puis de
, puis de  à
à 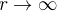 . Utiliser les expressions de
. Utiliser les expressions de 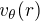 pour chaque domaine avant de simplifier.
pour chaque domaine avant de simplifier.
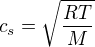 dans les expressions obtenues.
dans les expressions obtenues.
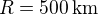 et de différence de pression en son centre avec la pression moyenne à la surface de Mars
et de différence de pression en son centre avec la pression moyenne à la surface de Mars 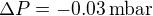 . Cette dépression se situe à la latitude
. Cette dépression se situe à la latitude  . On se placera par la suite dans le cadre de l'approximation géostrophique. La température moyenne sur Mars est voisine de
. On se placera par la suite dans le cadre de l'approximation géostrophique. La température moyenne sur Mars est voisine de 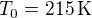 , la pression moyenne de surface voisine de
, la pression moyenne de surface voisine de 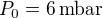 , l'accélération de la gravité y vaut
, l'accélération de la gravité y vaut 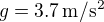 et la masse molaire de l'atmosphère y est de
et la masse molaire de l'atmosphère y est de 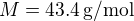 .
.
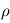 de l'atmosphère à la surface de Mars.
de l'atmosphère à la surface de Mars.
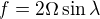 .
.
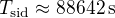 .
.
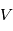 de la vitesse du vent tangentiel à la distance
de la vitesse du vent tangentiel à la distance 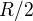 du centre de la dépression. Quelle sera sa direction ?
du centre de la dépression. Quelle sera sa direction ?
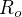 pour répondre à la question demandée.
pour répondre à la question demandée.
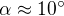 par rapport aux isobares (considérés ici comme des cercles concentriques). Exprimer le flux de masse gazeuse entrant par la surface latérale de la dépression, de périmètre
par rapport aux isobares (considérés ici comme des cercles concentriques). Exprimer le flux de masse gazeuse entrant par la surface latérale de la dépression, de périmètre 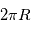 et s'étendant verticalement sur une échelle de hauteur
et s'étendant verticalement sur une échelle de hauteur 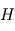 . En déduire alors la vitesse moyenne verticale du vent au sein de la dépression et son signe (ascendant ou descendant).
. En déduire alors la vitesse moyenne verticale du vent au sein de la dépression et son signe (ascendant ou descendant).
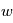 ) et juillet (
) et juillet (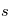 ) à différentes latitudes sur Terre.
) à différentes latitudes sur Terre.
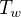 [°C]
[°C]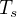 [°C]
[°C]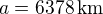 .
.
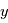 ici) se traduisent par des différences horizontales d'échelle de hauteur atmosphérique
ici) se traduisent par des différences horizontales d'échelle de hauteur atmosphérique 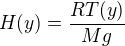 . En supposant les pression au niveau
. En supposant les pression au niveau 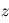 uniformes selon
uniformes selon 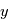 , montrer que les pressions à l'altitude
, montrer que les pressions à l'altitude  sont telles que :
sont telles que : 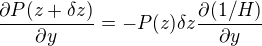
 , on peut linéariser l'équation hydrostatique décrivant la diminution de pression avec l'altitude :
, on peut linéariser l'équation hydrostatique décrivant la diminution de pression avec l'altitude : 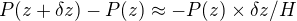 .
.
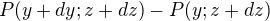 en utilisant le fait que
en utilisant le fait que 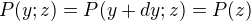 .
.
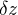 ) gradient horizontal de pression ainsi créé engendre un léger vent géostrophique
) gradient horizontal de pression ainsi créé engendre un léger vent géostrophique 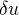 . Montrer que
. Montrer que 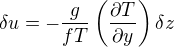 .
.
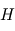 pour faire apparaître
pour faire apparaître 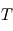 .
.
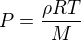 pour éliminer
pour éliminer 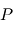 de l'équation géostrophique.
de l'équation géostrophique.
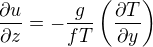 et s'appelle équation du vent thermique. Calculer le cisaillement vertical du vent zonal
et s'appelle équation du vent thermique. Calculer le cisaillement vertical du vent zonal 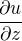 en utilisant cette équation. On donne la vitesse angulaire de la rotation sidérale terrestre
en utilisant cette équation. On donne la vitesse angulaire de la rotation sidérale terrestre 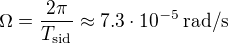 .
.
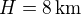 (soit environ une échelle de hauteur) en hiver puis en été. Dans quelle direction souffle ce vent (appelé courant jet) ?
(soit environ une échelle de hauteur) en hiver puis en été. Dans quelle direction souffle ce vent (appelé courant jet) ?
 .
.


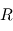 le rayon de l'anneau et
le rayon de l'anneau et 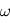 sa vitesse de rotation. On impose un gravité artificielle, c'est-à-dire une force centrifuge égale à
sa vitesse de rotation. On impose un gravité artificielle, c'est-à-dire une force centrifuge égale à 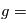 9.81
9.81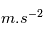 . On a donc la relation
. On a donc la relation 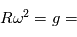 9.81
9.81 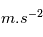 .
.
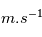 , on supposera ici que la vitesse maximale que peut atteindre un astronaute dans l'anneau est moitié moindre soit
, on supposera ici que la vitesse maximale que peut atteindre un astronaute dans l'anneau est moitié moindre soit  5
5 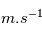 . On impose également que son poids ne doit pas varier de plus de 20 % lorsqu'il se déplace (imaginez courir et un cinquième de votre poids se rajoute à vous : c'est désagréable mais encore supportable).
. On impose également que son poids ne doit pas varier de plus de 20 % lorsqu'il se déplace (imaginez courir et un cinquième de votre poids se rajoute à vous : c'est désagréable mais encore supportable).
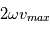 . Avec un critère de 10 % de variation du poids, on obtient la relation
. Avec un critère de 10 % de variation du poids, on obtient la relation 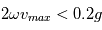
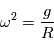 , on obtient
, on obtient 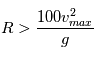 , soit un rayon minimal de 254 m.
, soit un rayon minimal de 254 m.