Pendant un temps dt, un planétésimal balaye le volume 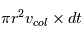 .
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par
.
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par 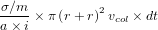 (m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3ρπr3 on obtient un taux
de collision de
(m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3ρπr3 on obtient un taux
de collision de 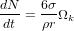 , où Ωk est la vitesse angulaire orbitale. Comme on suppose
que tous les planétésimaux ont toujours la même taille, on a donc, qu'à chaque collision, le
planétésimal accrète 1 fois sa propre masse. Donc
, où Ωk est la vitesse angulaire orbitale. Comme on suppose
que tous les planétésimaux ont toujours la même taille, on a donc, qu'à chaque collision, le
planétésimal accrète 1 fois sa propre masse. Donc 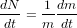 , ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule
, ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule 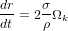 .
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance
.
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance 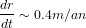 , soit environ 2.5 millions d'années pour
former un corps de 1000km.
, soit environ 2.5 millions d'années pour
former un corps de 1000km.
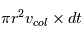 .
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par
.
Il faut maintenant estimer le nombre de planétésimaux contenus en moyenne dans ce volume.
Ce nombre est donné par 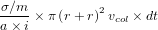 (m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3ρπr3 on obtient un taux
de collision de
(m étant
la masse d'un planétésimal). Le terme en (r + r)2 vient du fait que
même des corps dont le centre n'est pas dans le volume balayé par le planétésimal considéré
peuvent être impactés par lui en raison de leur taille non-nulle r.
En remplaçant vcol par e.vKep, e/i par 2 et
m par 4/3ρπr3 on obtient un taux
de collision de 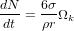 , où Ωk est la vitesse angulaire orbitale. Comme on suppose
que tous les planétésimaux ont toujours la même taille, on a donc, qu'à chaque collision, le
planétésimal accrète 1 fois sa propre masse. Donc
, où Ωk est la vitesse angulaire orbitale. Comme on suppose
que tous les planétésimaux ont toujours la même taille, on a donc, qu'à chaque collision, le
planétésimal accrète 1 fois sa propre masse. Donc 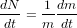 , ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule
, ce qui donne, en remplaçant dN/dt par la formule précédente et (1/m)*(dm/dt) par (3/r)*(dr/dt), la formule 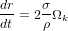 .
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance
.
On remarque que cette formule très simple ne dépend ni de e, ni de i,
ni de la taille des planétésimaux.
Et, à 1UA, cela donne un taux de croissance 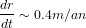 , soit environ 2.5 millions d'années pour
former un corps de 1000km.
, soit environ 2.5 millions d'années pour
former un corps de 1000km.