La condition la plus restrictive pour qu'une exoplanète soit dans la zone habitable - et donc potentiellement habitée par une vie détectable- est la présence d'eau liquide stable à sa surface. Notre expérience dans le Système Solaire / grâce aux premières observations d'exoplanètes montre qu'il existe une grande diversité de planètes. Pourtant, parmi cette diversité, la seule planète dont nous savons qu'elle possède de l'eau liquide stable depuis plus de 4 milliards d'années à sa surface est la Terre. Existe-t-il des planètes de configurations bien différentes de la Terre mais qui pourtant sont capables d'avoir de l'eau liquide stable à leur surface ? Si oui, à quoi ressemblent de telles exoplanètes ? Autour de quelles étoiles peut-on les trouver ? Quels gaz composent leur atmosphère ? ...
De nombreux paramètres
Flux lumineux reçu ; Composition, Taille et Masse de la planète ; Composition et Masse de l'atmosphère ; Paramètres orbitaux (excentricité, obliquité ...) de la planète ; Vitesse de rotation ... Ce sont tout autant de paramètres capables de favoriser ou non la présence d'eau stable à la surface d'une planète.
Il est extrêmement difficile de prédire à l'avance quel genre d'exoplanètes nous allons découvrir dans les années à venir.
Il est donc essentiel de comprendre, parmi tout ce panel de paramètres, quels sont ceux qui peuvent permettre à une planète ou non d'avoir de l'eau liquide stable et donc d'héberger de la vie.
Les différentes sortes d'atmosphères planétaires
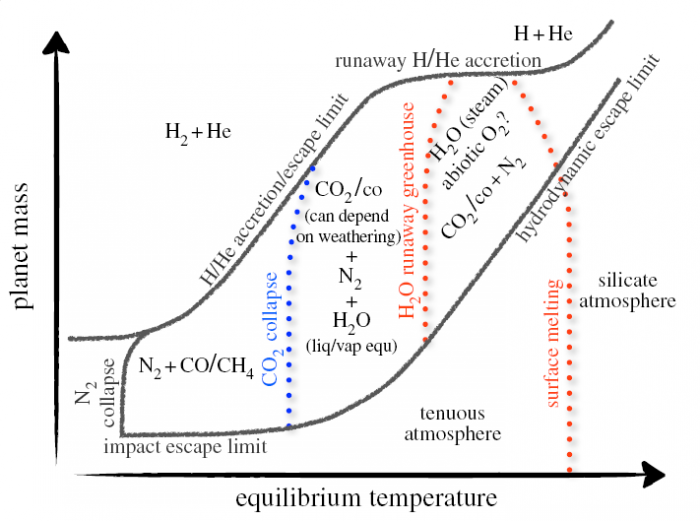
Diagramme représentant qualitativement les principales classes d'atmosphères qu'une planète puisse avoir en fonction de sa masse et de sa température de surface. Chaque trait (pointillé ou continu) délimite une transition entre deux classes possibles d'atmosphères.
Crédit :
F. Forget et J. Leconte
Vers une généralisation
Si vous connaissez par exemple la masse d'une planète et la distance qui la sépare de son étoile, il est possible de spéculer sur la nature et l'épaisseur de son atmosphère, élèments essentiels pour savoir si la planète peut potentiellement être habitable.
Imaginez une planète dans la Zone Habitable de son étoile, mais dont la masse serait 20 fois plus faible que celle de la Terre, comme Mercure par exemple. Dans ce cas, la planète n'exercera pas une gravité suffisante pour pouvoir garder une atmosphère capable de maintenir de l'eau liquide à sa surface.
Mais la masse d'une planète et sa distance à l'étoile ne sont pas des conditions suffisantes pour étudier son habitabilité. Il existe un grand nombre de configurations dans lesquelles une planète pourrait être habitable ... comme les planètes en rotation synchrone ? les planètes ayant une atmosphère d'hydrogène ? Les planètes ayant un flux géothermique très élevé ? ... Ce sont tout autant de candidats aux caractéristiques exotiques mais dont il faut explorer les possibilités ...
Les processus physiques qui entrent en jeu dans l'évolution du climat d'une planète sont nombreux. En voici une liste non-exhaustive :
- Equations de l'hydrodynamique (Navier Stokes) : Mouvement des parcelles d'air.
- Equations de la thermodynamique : Condensation, Evaporation, Solidification des constituants de la planète.
- Equations du transfert radiatif : Absorption, Emission, Réflection et Diffusion du flux solaire et du rayonnement thermique.
- Equations de microphysique : Physique des nuages.
- Equations chimiques : Photochimie.
La manière la plus réaliste de tenir compte de tous ces phénomènes physiques est d'utiliser un modèle de climat. Pour plus d'informations, veuillez vous reporter au cours sur les Modèles de Climat.
Modèle "Radiatif-Convectif" VS GCM
Dans un modèle Radiatif-Convectif, ou Modèle à 1 dimension, on représente la totalité de l'atmosphère d'une planète par une unique colonne composée d'un nombre discret de couches atmosphériques. Dans un GCM (Global Climate Model), ou Modèle à 3 dimensions, l'atmosphère est discrétisée selon les trois dimensions de l'espace.
Les modèles 3D ont l'avantage d'être plus complets et réalistes. Ils ont cependant le défaut d'être rapidement limités (par comparaison aux modèles 1D) par la puissance de calcul requis.
1D VS 3D : L'exemple de la température d'équilibre
Les modèles 1D comme celui-là ( accessible aussi là) sont plutôt fiables lorsqu'il s'agît de modéliser des planètes où la température de surface varie peu d'un point à un autre. C'est le cas des planètes avec une atmosphère très dense et/ou ayant une rotation suffisamment rapide. Dans le cas où il existe un contraste de température marqué entre deux points d'une même planète, le modèle 1D n'est plus représentatif de la planète. C'est notamment le cas des planètes en rotation synchrone, qui sont irradiées d'un côté (haute température) et pas de l'autre (basse température).
Prenons le cas d'une planète en rotation synchrone, sans atmosphère, en tout point à l'équilibre thermique, et avec un albédo de surface constant A. Et faisons l'hypothèse très simpliste qu'une face reçoit en tout point un flux solaire constant alors qu'une autre ne reçoit pas du tout de flux. Soit 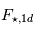 le flux moyen reçu sur l'ensemble de la surface. Le bilan radiatif 1D donne :
le flux moyen reçu sur l'ensemble de la surface. Le bilan radiatif 1D donne : 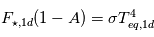 , soit
, soit 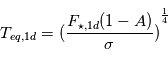 , avec
, avec 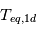 la température moyenne d'équilibre de la planète (1D).
la température moyenne d'équilibre de la planète (1D).
La planète est composée de deux faces d'aires égales : une éclairée et une autre non. Pour 50% de la planète, du côté de la face cachée, 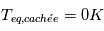 . Pour les 50% restants,
. Pour les 50% restants, 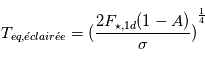 car le côté éclairé de la planète reçoit un flux lumineux deux fois plus élevé que le flux moyen reçu sur l'ensemble de la surface,
car le côté éclairé de la planète reçoit un flux lumineux deux fois plus élevé que le flux moyen reçu sur l'ensemble de la surface, 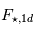 . La température moyenne d'équilibre de la planète (3D) vaut donc
. La température moyenne d'équilibre de la planète (3D) vaut donc 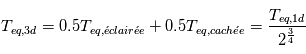 .
.
En bref, 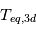 ~
~ 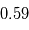
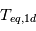 ! Pour ce cas particulier, l'erreur est considérable. En fait, de manière plus générale, plus l'écart-type sur la température d'équilibre d'une planète est grand, plus l'erreur commise sur le calcul de sa température de surface par un modèle 1D sera grande.
! Pour ce cas particulier, l'erreur est considérable. En fait, de manière plus générale, plus l'écart-type sur la température d'équilibre d'une planète est grand, plus l'erreur commise sur le calcul de sa température de surface par un modèle 1D sera grande.
Modèle 1D vs Modèle 3D, l'exemple
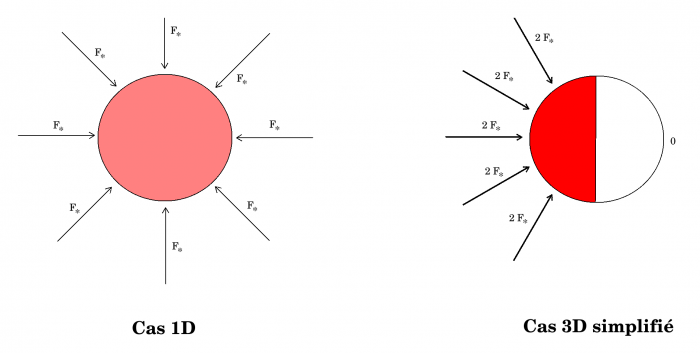
Cas d'une planète en rotation synchrone, sans atmosphère, en tout point à l'équilibre thermique, et avec un albédo de surface constant A. On fait l'hypothèse très simpliste qu'une face reçoit en tout point un flux solaire constant alors qu'une autre ne reçoit pas du tout de flux. Pour ce cas particulier, on montre que
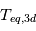
~
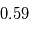
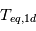
.
Crédit :
M. Turbet

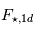 le flux moyen reçu sur l'ensemble de la surface. Le bilan radiatif 1D donne :
le flux moyen reçu sur l'ensemble de la surface. Le bilan radiatif 1D donne : 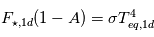 , soit
, soit 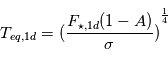 , avec
, avec 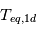 la température moyenne d'équilibre de la planète (1D).
la température moyenne d'équilibre de la planète (1D).
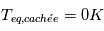 . Pour les 50% restants,
. Pour les 50% restants, 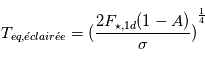 car le côté éclairé de la planète reçoit un flux lumineux deux fois plus élevé que le flux moyen reçu sur l'ensemble de la surface,
car le côté éclairé de la planète reçoit un flux lumineux deux fois plus élevé que le flux moyen reçu sur l'ensemble de la surface, 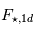 . La température moyenne d'équilibre de la planète (3D) vaut donc
. La température moyenne d'équilibre de la planète (3D) vaut donc 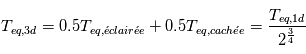 .
.
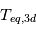 ~
~ 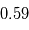
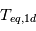 ! Pour ce cas particulier, l'erreur est considérable. En fait, de manière plus générale, plus l'écart-type sur la température d'équilibre d'une planète est grand, plus l'erreur commise sur le calcul de sa température de surface par un modèle 1D sera grande.
! Pour ce cas particulier, l'erreur est considérable. En fait, de manière plus générale, plus l'écart-type sur la température d'équilibre d'une planète est grand, plus l'erreur commise sur le calcul de sa température de surface par un modèle 1D sera grande.

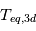 ~
~ 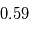
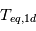 .
.