La datation absolue de roches anciennes est généralement réalisée grâce à la mesure de l'abondance d'éléments naturellement radioactifs. En effet, au cours du temps, l'abondance des noyaux parents décroît alors que celle des noyaux fils augmente. A un instant t, l'abondance des noyaux parents 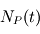 dépend de son abondance initiale
dépend de son abondance initiale 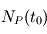 et de son temps caractéristique de décroissance
et de son temps caractéristique de décroissance 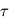 :
: 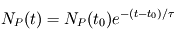 .
Il faut noter que le temps de demi-vie
.
Il faut noter que le temps de demi-vie 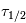 , qui correspond au temps nécessaire pour que l’abondance initiale soit divisée par deux, est souvent utilisé à la place du temps caractéristique de décroissance. Ces deux temps sont liés par la relation
, qui correspond au temps nécessaire pour que l’abondance initiale soit divisée par deux, est souvent utilisé à la place du temps caractéristique de décroissance. Ces deux temps sont liés par la relation 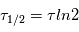 .
.
A l’instant t, l'abondance des noyaux fils 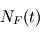 est égale à
est égale à 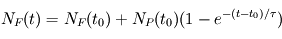 si tous les noyaux parents se désintègrent pour donner le même noyau fils. En combinant, les deux équations précédentes,
si tous les noyaux parents se désintègrent pour donner le même noyau fils. En combinant, les deux équations précédentes, 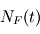 peut être exprimée en fonction de
peut être exprimée en fonction de 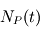 qui sont les deux quantités mesurables. Néanmoins,l'abondance initiale de noyaux fils
qui sont les deux quantités mesurables. Néanmoins,l'abondance initiale de noyaux fils 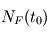 est généralement inconnue. La roche ayant pu subir une différentiation chimique lors de sa formation, elle peut être inhomogène. Les différentes mesures réalisées sur la même roche seront donc normalisées à l'abondance d'un isotope non radioactif de l'élément fils. En mesurant plusieurs échantillons de la même roche, l’âge de celle-ci ainsi que l'abondance initiale de l'élément fils radioactif pourront être déterminés (voir exercice dans la partie "Se Tester".).
est généralement inconnue. La roche ayant pu subir une différentiation chimique lors de sa formation, elle peut être inhomogène. Les différentes mesures réalisées sur la même roche seront donc normalisées à l'abondance d'un isotope non radioactif de l'élément fils. En mesurant plusieurs échantillons de la même roche, l’âge de celle-ci ainsi que l'abondance initiale de l'élément fils radioactif pourront être déterminés (voir exercice dans la partie "Se Tester".).
Un des couples d'éléments couramment utilisé est le couple 87Rb (élément parent) et 87Sr (élément fils), les abondances de ces deux éléments sont normalisées à l'abondance de 86Sr. Ces abondances sont mesurées par spectrométrie de masse en laboratoire. Les différentes mesures seront représentées dans un diagramme 87Sr / 86Sr en fonction de 87Rb / 86Sr. La pente de la droite obtenue 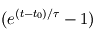 est liée à l’âge de formation de la roche alors que l’ordonnée à l’origine donne la rapport initial 87Sr / 86Sr. En normalisant à un isotope stable et en effectuant différentes mesures sur une roche hétérogène, les deux inconnues précédentes peuvent donc être déterminées et en particulier l’âge de la roche. Cette méthode n’est valable que si le système étudié, la roche ou la météorité, est clos, c’est-à-dire si aucun des éléments étudiés n’a pu diffuser à l’extérieur du système.
est liée à l’âge de formation de la roche alors que l’ordonnée à l’origine donne la rapport initial 87Sr / 86Sr. En normalisant à un isotope stable et en effectuant différentes mesures sur une roche hétérogène, les deux inconnues précédentes peuvent donc être déterminées et en particulier l’âge de la roche. Cette méthode n’est valable que si le système étudié, la roche ou la météorité, est clos, c’est-à-dire si aucun des éléments étudiés n’a pu diffuser à l’extérieur du système.
La datation absolue des météorites, et en particulier des inclusions les plus anciennes qu’elles contiennent, nous permet de dater la formation du système à 4.56 milliards d'années. Sans l'étude des météorites et des méthodes de datations liées aux isotopes naturellement radioactifs, l'obtention d'un chiffre aussi précis ne serait pas possible. L’étude des météorites et de l’ensemble des échantillons d’origine extra-terrestre disponibles au laboratoire permet donc de dater de manière absolue la formation du système solaire dans son ensemble.
L’atmosphère des comètes est appelée coma. La principale source des espèces gazeuses présentes autour des noyaux cométaires est la sublimation des glaces contenues dans celui-ci. Les molécules gazeuses produites directement depuis la surface ou la sous-surface du noyau sont appelées « molécules mères ». Une fois dans l’environnement cométaire ces molécules gazeuses sont soumises au flux ultraviolet du Soleil et peuvent se photo-dissocier en de nouvelles espèces gazeuses plus petites appelée « molécules filles ». Par exemple, la molécule d’eau peut se photo-dissocier en radicaux hydroxyle (OH) et en atomes d’hydrogène. La distribution spatiale autour du noyau est l'élément essentiel pour comprendre l’origine des espèces gazeuses. Afin de déterminer les mécanismes de production des différentes espèces gazeuses présentes dans la coma puis remonter aux abondances des molécules présentes dans le noyau ; les distributions spatiales mesurées grâce aux observations astronomiques doivent être comparées à un modèle. Le modèle le plus simple pour décrire la distribution spatiale des molécules est le modèle de Haser.
Dans le cadre du modèle de Haser, la densité des molécules mères dans la coma n’est régi que par l’expansion générale de la coma et par leur photolyse sous l’effet du rayonnement UV solaire. La densité volumique 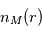 (en molécules.m-3) en fonction de la distance r au noyau, vérifie donc l’équation de conservation de la masse :
(en molécules.m-3) en fonction de la distance r au noyau, vérifie donc l’équation de conservation de la masse :
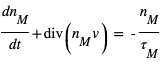 où
où 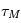 est la durée de vie de la molécule mère étudiée dans l’environnement cométaire et
est la durée de vie de la molécule mère étudiée dans l’environnement cométaire et 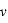 la vitesse d’expansion des gaz dans la coma.
la vitesse d’expansion des gaz dans la coma.
En supposant un état stationnaire, une vitesse constante dans la coma et une symétrie sphérique, l’équation précédente se simplifie :
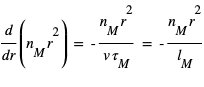 où
où 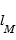 est appelée « longueur d’échelle parent », elle correspond à la longueur caractéristique de photolyse de la molécule mère.
est appelée « longueur d’échelle parent », elle correspond à la longueur caractéristique de photolyse de la molécule mère.
La condition initiale permettant d’intégrer l’équation différentielle précédente est donnée par le taux de production Q (en molécules.s-1) qui correspond au nombre de molécules mère émises depuis la surface du noyau en 1 seconde. L’intégration de l’équation précédente conduit à :
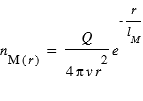 .
.
Pour les molécules filles, la densité volumique dans la coma est régi par les mêmes processus auxquels il faut rajouter la production directement dans la coma par photolyse de la molécule mère. Dans ce cas, l’équation de conservation de la masse s’écrit avec deux termes dans le membre de droite ; i.) un terme de production qui correspond à la photodissociation de la molécule mère et ii.) un second terme de destruction correspond à la photodissociation de l’espèce fille considérée.
Soit 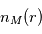 et
et 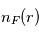 les densités volumiques des espèces mère et fille, ainsi que
les densités volumiques des espèces mère et fille, ainsi que 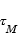 et
et 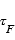 leurs temps de vie respectifs dans l’environnement cométaire. L’équation de conservation de la masse pour une espèce fille s’écrit alors :
leurs temps de vie respectifs dans l’environnement cométaire. L’équation de conservation de la masse pour une espèce fille s’écrit alors :
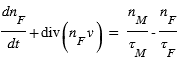 En utilisant les mêmes hypothèses géométriques et dynamiques que précédemment et en imposant la condition initiale n_F (0)=0, on trouve :
En utilisant les mêmes hypothèses géométriques et dynamiques que précédemment et en imposant la condition initiale n_F (0)=0, on trouve :
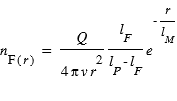 .
Dans cette dernière équation, Q est le taux de production de la molécule mère dont est issue la molécule fille,
.
Dans cette dernière équation, Q est le taux de production de la molécule mère dont est issue la molécule fille, 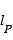 la longueur d’échelle parent et
la longueur d’échelle parent et 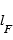 la longueur d’échelle fille qui correspondent respectivement aux longueurs caractéristiques de destruction par photolyse des espèces mère et fille.
la longueur d’échelle fille qui correspondent respectivement aux longueurs caractéristiques de destruction par photolyse des espèces mère et fille.
Ce modèle est très simple, voir simpliste au regard de nos connaissances actuelles sur les comètes. En particulier, la production de gaz à la surface du noyau est inhomogène et les environnements cométaire n’ont pas une symétrie sphérique. Néanmoins, ce modèle permet d’obtenir des ordres de grandeurs pertinents en particulier pour les longueurs d’échelles et des versions modifiées de ce modèle continuent à être utilisées pour calculer les taux de production des espèces gazeuses à partir des observations.
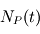 dépend de son abondance initiale
dépend de son abondance initiale 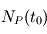 et de son temps caractéristique de décroissance
et de son temps caractéristique de décroissance 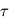 :
: 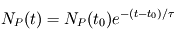 .
Il faut noter que le temps de demi-vie
.
Il faut noter que le temps de demi-vie 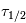 , qui correspond au temps nécessaire pour que l’abondance initiale soit divisée par deux, est souvent utilisé à la place du temps caractéristique de décroissance. Ces deux temps sont liés par la relation
, qui correspond au temps nécessaire pour que l’abondance initiale soit divisée par deux, est souvent utilisé à la place du temps caractéristique de décroissance. Ces deux temps sont liés par la relation 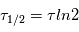 .
.
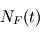 est égale à
est égale à 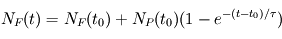 si tous les noyaux parents se désintègrent pour donner le même noyau fils. En combinant, les deux équations précédentes,
si tous les noyaux parents se désintègrent pour donner le même noyau fils. En combinant, les deux équations précédentes, 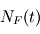 peut être exprimée en fonction de
peut être exprimée en fonction de 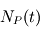 qui sont les deux quantités mesurables. Néanmoins,l'abondance initiale de noyaux fils
qui sont les deux quantités mesurables. Néanmoins,l'abondance initiale de noyaux fils 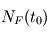 est généralement inconnue. La roche ayant pu subir une différentiation chimique lors de sa formation, elle peut être inhomogène. Les différentes mesures réalisées sur la même roche seront donc normalisées à l'abondance d'un isotope non radioactif de l'élément fils. En mesurant plusieurs échantillons de la même roche, l’âge de celle-ci ainsi que l'abondance initiale de l'élément fils radioactif pourront être déterminés (voir exercice dans la partie "Se Tester".).
est généralement inconnue. La roche ayant pu subir une différentiation chimique lors de sa formation, elle peut être inhomogène. Les différentes mesures réalisées sur la même roche seront donc normalisées à l'abondance d'un isotope non radioactif de l'élément fils. En mesurant plusieurs échantillons de la même roche, l’âge de celle-ci ainsi que l'abondance initiale de l'élément fils radioactif pourront être déterminés (voir exercice dans la partie "Se Tester".).
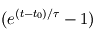 est liée à l’âge de formation de la roche alors que l’ordonnée à l’origine donne la rapport initial 87Sr / 86Sr. En normalisant à un isotope stable et en effectuant différentes mesures sur une roche hétérogène, les deux inconnues précédentes peuvent donc être déterminées et en particulier l’âge de la roche. Cette méthode n’est valable que si le système étudié, la roche ou la météorité, est clos, c’est-à-dire si aucun des éléments étudiés n’a pu diffuser à l’extérieur du système.
est liée à l’âge de formation de la roche alors que l’ordonnée à l’origine donne la rapport initial 87Sr / 86Sr. En normalisant à un isotope stable et en effectuant différentes mesures sur une roche hétérogène, les deux inconnues précédentes peuvent donc être déterminées et en particulier l’âge de la roche. Cette méthode n’est valable que si le système étudié, la roche ou la météorité, est clos, c’est-à-dire si aucun des éléments étudiés n’a pu diffuser à l’extérieur du système.
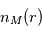 (en molécules.m-3) en fonction de la distance r au noyau, vérifie donc l’équation de conservation de la masse :
(en molécules.m-3) en fonction de la distance r au noyau, vérifie donc l’équation de conservation de la masse :
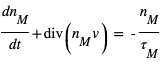 où
où 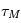 est la durée de vie de la molécule mère étudiée dans l’environnement cométaire et
est la durée de vie de la molécule mère étudiée dans l’environnement cométaire et 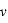 la vitesse d’expansion des gaz dans la coma.
la vitesse d’expansion des gaz dans la coma.
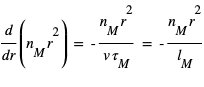 où
où 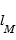 est appelée « longueur d’échelle parent », elle correspond à la longueur caractéristique de photolyse de la molécule mère.
est appelée « longueur d’échelle parent », elle correspond à la longueur caractéristique de photolyse de la molécule mère.
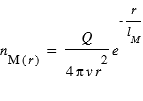 .
.
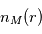 et
et 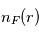 les densités volumiques des espèces mère et fille, ainsi que
les densités volumiques des espèces mère et fille, ainsi que 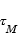 et
et 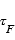 leurs temps de vie respectifs dans l’environnement cométaire. L’équation de conservation de la masse pour une espèce fille s’écrit alors :
leurs temps de vie respectifs dans l’environnement cométaire. L’équation de conservation de la masse pour une espèce fille s’écrit alors :
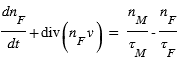 En utilisant les mêmes hypothèses géométriques et dynamiques que précédemment et en imposant la condition initiale n_F (0)=0, on trouve :
En utilisant les mêmes hypothèses géométriques et dynamiques que précédemment et en imposant la condition initiale n_F (0)=0, on trouve :
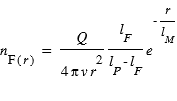 .
Dans cette dernière équation, Q est le taux de production de la molécule mère dont est issue la molécule fille,
.
Dans cette dernière équation, Q est le taux de production de la molécule mère dont est issue la molécule fille, 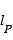 la longueur d’échelle parent et
la longueur d’échelle parent et 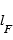 la longueur d’échelle fille qui correspondent respectivement aux longueurs caractéristiques de destruction par photolyse des espèces mère et fille.
la longueur d’échelle fille qui correspondent respectivement aux longueurs caractéristiques de destruction par photolyse des espèces mère et fille.