Auteur: EM
 Une autre interprétation de l'échelle de hauteur
Une autre interprétation de l'échelle de hauteur
Difficulté : ☆
Temps : 30 min
Question 1)
Exprimer la masse 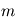 d'une colonne d'atmosphère de surface
d'une colonne d'atmosphère de surface 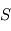 en fonction de la pression à la surface
en fonction de la pression à la surface 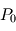 et de l'accélération de la gravité
et de l'accélération de la gravité 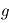 . Faire l'application numérique approchée dans le cas de la Terre.
. Faire l'application numérique approchée dans le cas de la Terre.
[3 points]
Se souvenir de la signfication physique de la loi hydrostatique : quelle est l'origine physique de la pression atmosphérique ?
Question 3)
En utilisant l'équation d'état du gaz parfait, exprimer alors 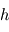 en fonction notamment de
en fonction notamment de 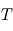 et de la masse molaire
et de la masse molaire 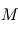 du gaz.
du gaz.
[2 points]
Considérer la forme intensive de l'équation d'état du gaz parfait, à savoir 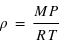 .
.
Question 4)
En déduire une nouvelle interprétation de l'échelle de hauteur atmosphérique.
[1 points]
Constater l'égalité obtenue précédemment entre 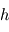 et l'échelle de hauteur telle que définie dans le cours.
et l'échelle de hauteur telle que définie dans le cours.
Auteur: EM
 Zone d'habitabilité du système TRAPPIST-1
Zone d'habitabilité du système TRAPPIST-1
Difficulté : ☆
Temps : 30 min
Voici un tableau résumant les caractéristiques des planètes connues (en 2017) du système TRAPPIST-1. L'étoile centrale est une naine rouge ultrafroide (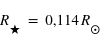 et
et 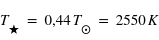 )
)
Caractéristiques des planètes du système TRAPPIST-1
| Nom | Masse (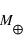 ) ) | Rayon (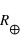 ) ) | Distance 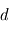 à l'étoile (UA) à l'étoile (UA) | 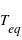 (K) (K) |
|---|
| b | 0.79 | 1.086 | 0.01111 | |
| c | 1.63 | 1.056 | 0.01522 | |
| d | 0.33 | 0.772 | 0.02145 | |
| e | 0.24 | 0.918 | 0.02818 | |
| f | 0.36 | 1.045 | 0.0371 | |
| g | 0.566 | 1.127 | 0.0451 | |
| h | 0.086 | 0.715 | 0.0596 | |
Question 2)
Même question dans le cas où on considère un albédo nul pour ces planètes. Commenter.
[2 points]
Utiliser la même méthode qu'à la question précédente, mais en ne simplifiant pas l'albédo terrestre.
Question 3)
Les limites de la zone d'habitabilité dans le système solaire sont de 0,95 UA (bord interne ; plus près, le flux stellaire trop important entraîne un effet de serre divergent pour la vapeur d'eau) et 1,37 UA (bord externe ; plus loin, même l'effet de serre d'une atmosphère riche en CO2 ne permet plus de maintenir des températures de surface au-dessus de 0°C). Calculer les limites correspondantes pour le système TRAPPIST-1. Quelles planètes pourraient alors être habitables ?
[2 points]
Raisonner en températures d'équilibre ou en flux stellaire est strictement équivalent ici.
Question 4)
Compléter le tableau ci-dessus en indiquant, pour chaque planète (supposées d'albédo terrestre) ainsi que pour l'étoile TRAPPIST-1, la longueur d'one du maximum de son émission thermique. Comparer avec la situation du système solaire.
[1 points]
Utiliser la loi de Wien rappelée dans le cours.
Auteur: EM
 Temps radiatif dans une atmosphère
Temps radiatif dans une atmosphère
Difficulté : ☆☆☆
Temps : 45 min
On considère une atmosphère transparente en lumière visible et partiellement opaque aux IR thermiques (absorbance et émissivité 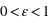 ), et de température uniforme
), et de température uniforme 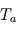 à l'équilbre radiatif. À l'instant intial, on perturbe la température de cette atmosphère d'une quantité
à l'équilbre radiatif. À l'instant intial, on perturbe la température de cette atmosphère d'une quantité 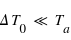 .
. 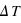 varie ensuite en fonction du temps.
varie ensuite en fonction du temps.
Question 1)
Pourquoi peut considérér que l'absorbance et l'émissivité de l'atmosphère sont égales (pour une longueur d'onde donnée) ?
[1 points]
Question 2)
Exprimer le surcroît de flux thermique 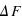 émis par une colonne atmosphérique de surface
émis par une colonne atmosphérique de surface 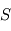 dans tout l'espace. On se limitera à l'ordre 1 en
dans tout l'espace. On se limitera à l'ordre 1 en 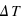 .
.
[2 points]
Ne pas oublier que le flux est émis dans les deux demi-espaces (vers le haut et vers le bas) !
Penser à effectuer un développement limité.
Question 3)
Exprimer la capacité calorifique (à pression constante)  de cette colonne d'atmosphère en fonction notamment de la capacité calorifique massique
de cette colonne d'atmosphère en fonction notamment de la capacité calorifique massique 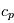 , de la pression de surface
, de la pression de surface 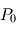 et de la gravité de surface
et de la gravité de surface 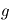 .
.
[1 points]
Exprimer d'abord la masse de cette colonne d'air au moyen de la loi hydrostatique (voir exercice sur l'échelle de hauteur).
Question 4)
Montrer alors que 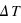 obéit à l'équation différentielle suivante :
obéit à l'équation différentielle suivante : 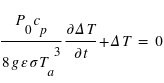
[2 points]
Effectuer un bilan d'énergie sur la colonne d'atmosphère considérée.
Question 5)
Résoudre alors cette équation en faisant apparaître une constante de temps appelée temps radiatif 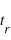 .
.
[1 points]
Appliquer des arguments d'analyse dimensionnelle à l'équation différentielle obtenue précédemment.
Question 7)
Estimer alors l'amplitude thermique diurne de température sur Terre et sur Mars.
[2 points]
Quelle serait la nouvelle température d'équilibre si la nuit devait durer pour toujours ? Comment évoluerait alors la température de l'atmosphère ?
Auteur: Emmanuel Marcq
 Exercice
Exercice
Vous venez d'être embauché par un célèbre réalisateur Hollywoodien en tant que conseiller scientifique pour son prochain film de science-fiction. L'action se déroulera sur une lune tellurique nommée Pandore d'une planète géante appelée Polyphème en orbite autour de l'étoile 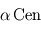 . Toutes les données numériques pertinentes se trouvent ci-dessous.
. Toutes les données numériques pertinentes se trouvent ci-dessous.
Données numériques pertinentes
Étoile (α Centauri) :
- Masse : 1,1 masse solaire
- Rayon : 1,27 rayon solaire
- Classe spectrale : G2V
- Température photosphérique : 5790 K
Polyphème :
- Masse : 0,44 masse jovienne
- Rayon : 0,75 rayon jovien
- Période de rotation : 15 h
- Période de révolution : 1,4 année terrestre
- Rayon de l'orbite : 1,32 UA
- Albédo visible : 0.4
Pandore :
- Rayon : 0,78 rayon terrestre
- Masse : 0,43 masse terrestre
- Rayon de l'orbite : 264000 km
- Période de rotation (synchrone avec révolution) : 31,5 h
- Albédo visible : 0,3
- Pression atmosphérique à la surface : 1,22 bar
- Température moyenne de surface : 27°C
- Composition atmosphérique (% en masse) :
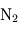 (81 %),
(81 %), 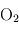 (16 %),
(16 %), 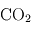 (2 %),
(2 %), 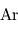 (1 %),
(1 %), 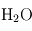 (variable),
(variable), 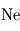 ,
, 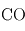 ,
, 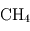 ,
, 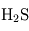 ,
, 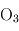 ,
, 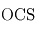 ,
, 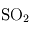 (traces).
(traces). - Capacité calorifique à pression constante : 1012 J/kg/K
Question 1)
- Quelle est la puissance lumineuse totale émise par l'étoile hôte ?
- Calculer alors la constante stellaire au niveau de l'orbite de Polyphème.
- Considérer l'étoile comme un corps noir ;
- et que la puissance émise se dilue uniformément dans l'espace jusqu'au niveau de l'orbite de Polyphème.
Question 6)
Compte tenu de la composition atmosphérique, s'attend-on à trouver une stratosphère sur Pandore ? Si oui, quelle serait l'espèce chimique responsable ?
Chercher parmi les espèces présentes celles qui absorbent les UV, et comparer leurs abondances à celle des espèces qui rayonnent bien dans l'IR thermique.
Question 8)
Calculer le gradient adiabatique sec 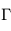 . Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
. Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
Applications directes des formules du cours.
Question 9)
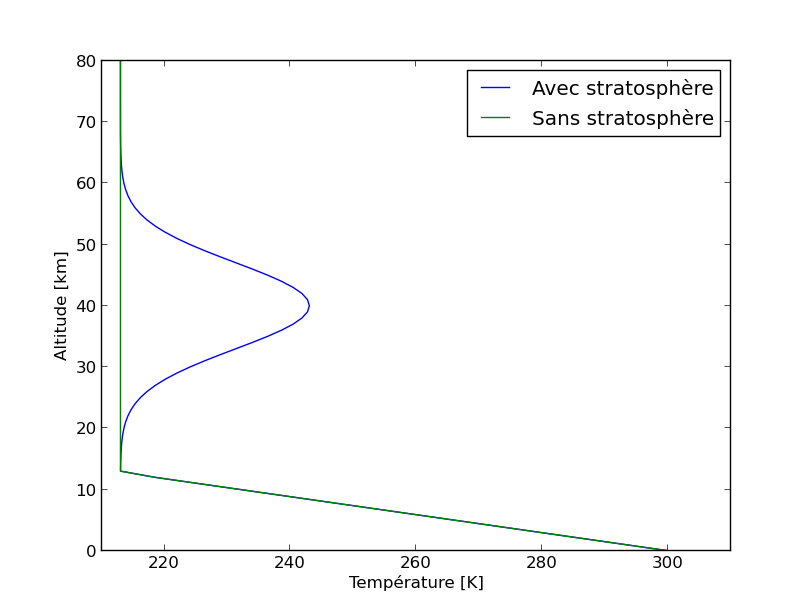
Représenter l'allure du profil thermique moyen de Pandore. On considérera que la troposphère s'étend sur une échelle de hauteur 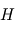 , et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
, et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
Températures importantes : au sommet de la troposphère, au sommet de l'atmosphère (voir le modèle à deux couches).
- Question 1
Aide :
- Considérer l'étoile comme un corps noir ;
- et que la puissance émise se dilue uniformément dans l'espace jusqu'au niveau de l'orbite de Polyphème.
Solution :
- 6,25 1026 W
- 1269 W/m2
- Question 2
Aide :
- Utiliser la définition.
- Une planète géante dispose en général d'une source d'énergie interne importante.
- Examiner quelles espèces chimiques courantes sont condensables à cette température.
Solution :
- 241 K
- Supérieure.
- Glace d'eau ou ammoniaque liquide.
- Question 3
Aide :
Ce sont des applications directes des définitions.
Solution :
- 250 K, qui est aussi est la température effective.
- La température de surface est plus élevée de 50 K par rapport à la température effective : le responsable en est l'effet de serre.
- Question 4
Aide :
- Le schéma est une version simplifiée de celui du cours.
- Il s'agit d'une simple identification.
- À l'équilibre, le flux absorbé est égal au flux émis.
- Le flux solaire absorbé s'exprime simplement avec la température effective.
- Le signe du désaccord est important.
Solution :
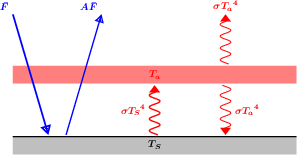
- Cela donne
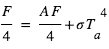 , d'où
, d'où 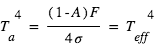 et donc
et donc 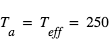 K
K 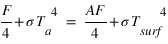
- Comme
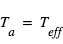 on déduit du bilan donné en 3 que
on déduit du bilan donné en 3 que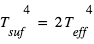 d'où
d'où 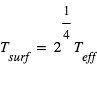
- La température de surface calculée est de 297,5 K, soit légèrement inférieure aux 300 K données dans l'énoncé. L'effet de serre à une couche est donc sous-estimé, il faut passer à un modèle plus complexe.
- Question 5
Aide :
- S'inspirer du schéma du mini-projet.
- Chaque sous-système (couche atmosphérique ou surface) se trouve à l'équilibre radiatif : le bilan global des flux doit être équilibré.
- On calculera
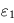 en fonction de
en fonction de 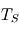 que l'énoncé donne, puis on injectera la valeur de
que l'énoncé donne, puis on injectera la valeur de 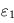 dans les expressions de
dans les expressions de 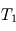 et
et 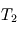 .
. - Comparer le nombre de couches nécessaires.
Solution :
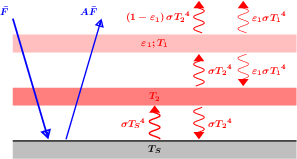
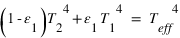 ,
, 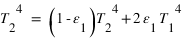 et
et 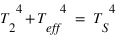
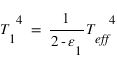 ,
, 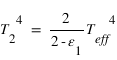 et
et 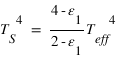 . D'où
. D'où 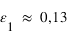 ,
,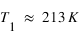 et
et 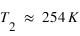 .
. - Il faut donc entre une et deux couches opaques aux infrarouges pour rendre compte de l'effet de serre sur Pandore, tandis que moins d'une couche opaque est nécessaire pour la Terre : l'effet de serre sur Pandore est supérieur à l'effet de serre sur Terre.
- Question 6
Aide :
Chercher parmi les espèces présentes celles qui absorbent les UV, et comparer leurs abondances à celle des espèces qui rayonnent bien dans l'IR thermique.
Solution :
Les bons absorbants en UV sont l'ozone et le dioxyde de soufre, tandis que le dioxyde de carbone, la vapeur d'eau, le méthane et le monoxyde de carbone sont de bons gaz à effet de serre. L'existence d'une stratosphère est donc possible, même si probablement moins marquée que sur Terre du fait du plus grand effet de serre.
- Question 7
Aide :
- Ce sont des savoir-faire élémentaires de chimie et de mécanique de point.
- Appliquer la définition du cours.
- Se souvenir de la loi d'évolution de la pression en fonction de l'altitude dans le cas isotherme.
Solution :
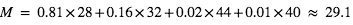 g/mol .
g/mol . 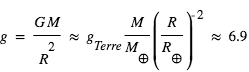 m/s2
m/s2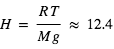 km
km- On a
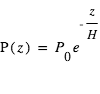 en supposant l'échelle de hauteur constante, d'où
en supposant l'échelle de hauteur constante, d'où 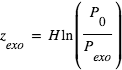 avec
avec 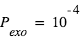 Pa,
Pa, 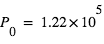 Pa et H = 12.4 km. On trouve H ≈ 260 km
Pa et H = 12.4 km. On trouve H ≈ 260 km
- Question 8
Aide :
Applications directes des formules du cours.
Solution :
-6,8 K/km. Le gradient adiabatique humide sera inférieur en valeur absolue.
- Question 9
Aide :
Températures importantes : au sommet de la troposphère, au sommet de l'atmosphère (voir le modèle à deux couches).
Solution :
 Une autre interprétation de l'échelle de hauteur
Une autre interprétation de l'échelle de hauteur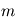 d'une colonne d'atmosphère de surface
d'une colonne d'atmosphère de surface 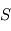 en fonction de la pression à la surface
en fonction de la pression à la surface 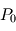 et de l'accélération de la gravité
et de l'accélération de la gravité 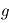 . Faire l'application numérique approchée dans le cas de la Terre.
. Faire l'application numérique approchée dans le cas de la Terre.
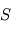 et de hauteur
et de hauteur 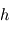 au sein de laquelle la pression est partout égale à
au sein de laquelle la pression est partout égale à 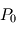 et la température partout égale à
et la température partout égale à 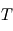 . Cette boîte contient en outre la même masse
. Cette boîte contient en outre la même masse 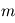 de gaz que la colonne d'atmosphère considérée à la question précédente.
de gaz que la colonne d'atmosphère considérée à la question précédente.
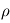 du gaz contenu dans la boîte en fonction de
du gaz contenu dans la boîte en fonction de 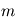 , puis en fonction de
, puis en fonction de 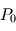 .
.
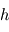 en fonction notamment de
en fonction notamment de 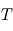 et de la masse molaire
et de la masse molaire 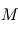 du gaz.
du gaz.
 Zone d'habitabilité du système TRAPPIST-1
Zone d'habitabilité du système TRAPPIST-1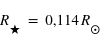 et
et 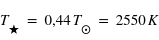 )
)
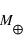 )
)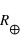 )
)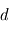 à l'étoile (UA)
à l'étoile (UA)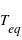 (K)
(K)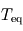 du tableau en supposant que toutes ces planètes ont le même albédo bolométrique que la Terre. On donne pour la Terre
du tableau en supposant que toutes ces planètes ont le même albédo bolométrique que la Terre. On donne pour la Terre 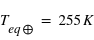 et
et 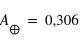 .
.
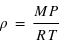 .
.
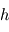 et l'échelle de hauteur telle que définie dans le cours.
et l'échelle de hauteur telle que définie dans le cours.
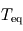 en fonction de la température effective
en fonction de la température effective 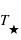 de l'étoile, et faire le rapport avec son application au cas de la Terre autour du Soleil.
de l'étoile, et faire le rapport avec son application au cas de la Terre autour du Soleil.
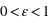 ), et de température uniforme
), et de température uniforme 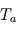 à l'équilbre radiatif. À l'instant intial, on perturbe la température de cette atmosphère d'une quantité
à l'équilbre radiatif. À l'instant intial, on perturbe la température de cette atmosphère d'une quantité 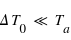 .
. 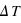 varie ensuite en fonction du temps.
varie ensuite en fonction du temps.
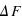 émis par une colonne atmosphérique de surface
émis par une colonne atmosphérique de surface 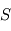 dans tout l'espace. On se limitera à l'ordre 1 en
dans tout l'espace. On se limitera à l'ordre 1 en 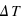 .
.
 de cette colonne d'atmosphère en fonction notamment de la capacité calorifique massique
de cette colonne d'atmosphère en fonction notamment de la capacité calorifique massique 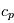 , de la pression de surface
, de la pression de surface 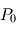 et de la gravité de surface
et de la gravité de surface 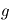 .
.
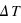 obéit à l'équation différentielle suivante :
obéit à l'équation différentielle suivante : 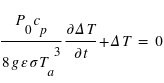
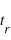 .
.
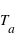 [K]
[K]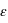
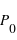 [Pa]
[Pa]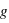 [m/s²]
[m/s²]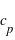 [J/K/kg]
[J/K/kg]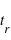 pour ces deux planètes.
pour ces deux planètes.
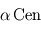 . Toutes les données numériques pertinentes se trouvent ci-dessous.
. Toutes les données numériques pertinentes se trouvent ci-dessous.
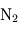 (81 %),
(81 %), 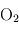 (16 %),
(16 %), 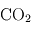 (2 %),
(2 %), 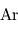 (1 %),
(1 %), 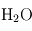 (variable),
(variable), 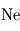 ,
, 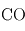 ,
, 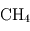 ,
, 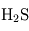 ,
, 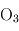 ,
, 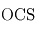 ,
, 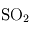 (traces).
(traces).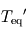 de la planète géante
de la planète géante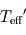 de Polyphème sera-t-elle supérieure ou inférieure à
de Polyphème sera-t-elle supérieure ou inférieure à 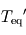 ? Justifier.
? Justifier.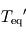 .
.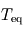 de Pandore. La comparer à celle du point triple de l'eau, égale à
de Pandore. La comparer à celle du point triple de l'eau, égale à 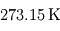 . Que vaut alors
. Que vaut alors 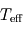 ?
?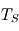 et
et 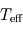 ? En donner une explication qualitative.
? En donner une explication qualitative.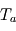 .
.
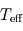 .
.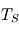 et
et 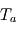 en fonction de
en fonction de 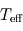 .
.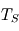 donnée dans l'énoncé. Que constate-t-on ? Proposer une explication.
donnée dans l'énoncé. Que constate-t-on ? Proposer une explication.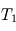 et celle de la couche profonde
et celle de la couche profonde 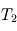 . La couche 1 absorbe une fraction
. La couche 1 absorbe une fraction 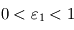 du rayonnement IR thermique. Ces deux couches sont toujours considérées parfaitement transparentes en lumière visible.
du rayonnement IR thermique. Ces deux couches sont toujours considérées parfaitement transparentes en lumière visible.
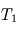 ,
, 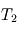 et
et 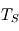 . On fera apparaître l'expression de
. On fera apparaître l'expression de 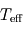 dans ce système.
dans ce système.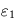 , puis celles de
, puis celles de 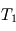 et
et 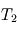 .
.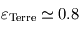 ). Comparer l'intensité de l'effet de serre sur Terre et sur Pandore.
). Comparer l'intensité de l'effet de serre sur Terre et sur Pandore.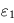 en fonction de
en fonction de 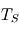 que l'énoncé donne, puis on injectera la valeur de
que l'énoncé donne, puis on injectera la valeur de 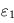 dans les expressions de
dans les expressions de 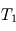 et
et 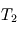 .
. 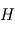 au niveau de la surface.
au niveau de la surface.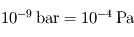 . Estimer l'altitude de cette exobase (on considérera
. Estimer l'altitude de cette exobase (on considérera 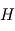 constant pour ce calcul).
constant pour ce calcul).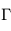 . Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
. Le gradient adiabatique humide sera-t-il inférieur ou supérieur en valeur absolue ?
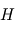 , et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.
, et on fera figurer l'échelle de hauteur, les différentes couches atmosphériques et les températures à leurs limites quand cela est possible.

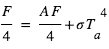 , d'où
, d'où 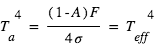 et donc
et donc 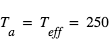 K
K 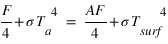
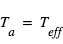 on déduit du bilan donné en 3 que
on déduit du bilan donné en 3 que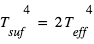 d'où
d'où 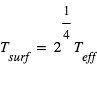

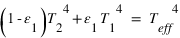 ,
, 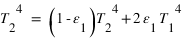 et
et 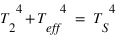
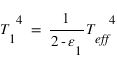 ,
, 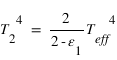 et
et 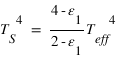 . D'où
. D'où 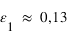 ,
,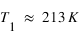 et
et 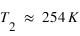 .
. 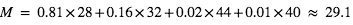 g/mol .
g/mol . 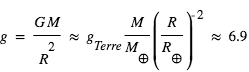 m/s2
m/s2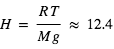 km
km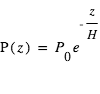 en supposant l'échelle de hauteur constante, d'où
en supposant l'échelle de hauteur constante, d'où 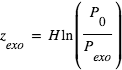 avec
avec 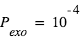 Pa,
Pa, 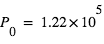 Pa et H = 12.4 km. On trouve H ≈ 260 km
Pa et H = 12.4 km. On trouve H ≈ 260 km