Pupille d'entrée et sa transformée de Fourier.
Crédit :
ASM
La TF de la pupille
La figure de diffraction d'une pupille, quelle qu'elle soit, est identique à sa transformée de Fourier.
La figure de diffraction d'une pupille, quelle qu'elle soit, est identique à sa transformée de Fourier.
PrérequisCours sur la diffraction de Fraunhofer.
Objectifs(Page à n'aborder qu'en 2eme lecture.) Mettre en regard le formalisme décrivant la diffraction à l'infini par une pupille et le formalisme de la transformation de Fourier.
En repérant un point de la pupille par la variable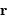 
, la fonction 
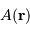caractérisant l'éclairement sur la pupille, l'amplitude diffractée
dans une direction angulaire de vecteur directeur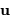 
s'écrit :
![\begin{eqnarray*} A ( \mathbf{u})\ &=&\ \int\!\!\!\int_{\mathrm{ pupille }} A( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right] \ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}\\ &=& \ \int\!\!\!\int {\cal P}( \mathbf{r})\ I( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right]\ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-fourier/equation4.png)
Avec le terme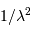 
introduit pour normaliser l'élément de surface 
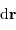, et
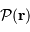la pupille d'entrée, qui limite la fraction de l'onde plane
émise par la source à l'infini. Pour un éclairement uniforme en incidence normale,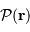 
est typiquement une fonction porte à 2 dimensions.
Par ailleurs, le formalisme de la transformation de Fourier s'écrit :
![\tilde f ( \mathbf{u}) \ =\ \int\!\!\!\int f( \mathbf{r} ) \exp\left[ -2i\pi \mathbf{u} . \mathbf{r} \right] \ \ {\mathrm{d}} \mathbf{r}](../pages_rayon/equations_diffraction-fourier/equation9.png)
On se doute que l'air de ressemblance entre ces 2 dernières égalités vaut plus qu'un simple hasard.
Si l'on peut supposer l'éclairement uniforme, l'amplitude diffractée dans une direction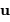 
est donnée par la transformée de Fourier de la fonction
de pupille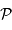 
, la variable de position étant normalisée en unité de longueur d'onde :
![A ( \mathbf{u})\ =\ A_0 \ \int\!\!\!\int {\cal P}( \mathbf{r})\ \exp\left[ -2i\pi \mathbf{u}. { \mathbf{r} \over \lambda} \right]\ \ { {\mathrm{d}} \mathbf{r}\over \lambda^2}](../pages_rayon/equations_diffraction-fourier/equation12.png)
Les variables conjuguées sont la direction angulaire, repérée par le vecteur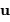 
, et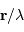 
la variable spatiale décrivant la pupille rapportée à la longueur d'onde.
On peut utiliser les propriétés de la TF pour réécrire les caractéristiques de la diffraction.
Une pupille de taille caractéristique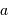 
filtre les hautes fréquences, càd l'information angulaire plus fine typiquement que 
.
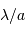Plus la pupille est grande, moins elle filtre angulairement.
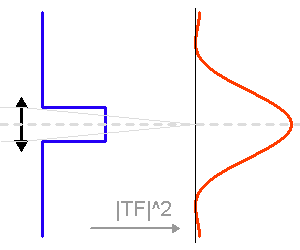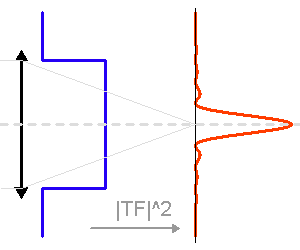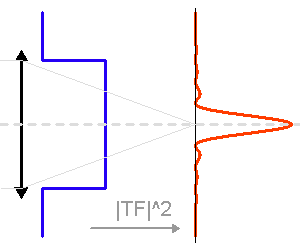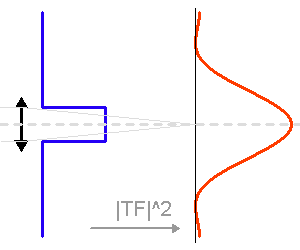
La tache image due à la seule diffraction dépend du diamètre du télescope. Plus ce dernier est grand, plus la tache d'Airy est piquée.