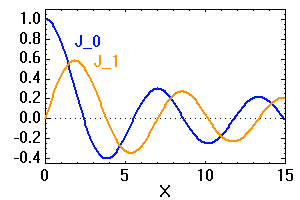
Les 2 premières fonctions de Bessel,
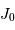
et
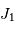
.
Crédit :
ASM
Fonctions de Bessel
La figure de diffraction d'une pupille circulaire introduit les fonctions de Bessel.
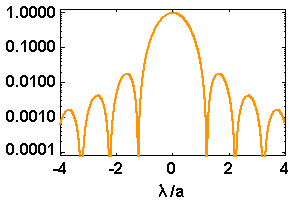
Coupe de la figure de diffraction, en représentation logarithmique et unité
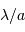
. Le premier zéro est à l'abscisse 1.22.
Crédit :
ASM
 Prérequis
Prérequis
Diffraction de Fraunhofer.
 Objectifs
Objectifs
(Page à n'aborder qu'en deuxième lecture).
Introduire, pour une pupille circulaire, les fonctions de Bessel, qui justifient le facteur 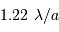 qui dimensionne la tache de diffraction.
qui dimensionne la tache de diffraction.
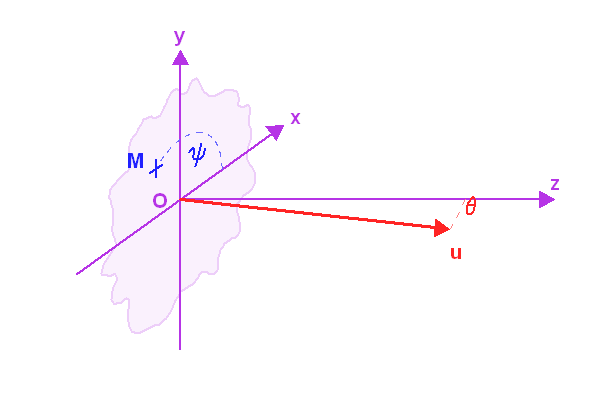
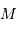
est un point courant de la pupille, de coordonnées polaires
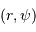
, et
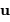
porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
Crédit :
ASM
Pupille circulaire
La pupille étant circulaire, de rayon 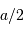 , il est préférable de décrire les coordonnées du point
, il est préférable de décrire les coordonnées du point 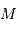 et de la direction de diffraction
et de la direction de diffraction  en coordonnées polaires, avec les notations suivantes :
en coordonnées polaires, avec les notations suivantes :
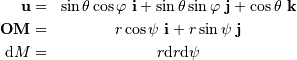
(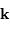 est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction
est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction 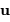 faisant un angle
faisant un angle 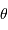 avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
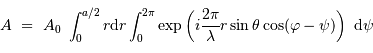
On introduit les fonctions de Bessel, dont les 2 premiers termes sont, par définition :
![\begin{eqnarray*} J_0 (X) =& \displaystyle{{1\over 2\pi} \int_0^{2\pi} \exp \bigl[-iX \cos v \bigr]\ {\mathrm{d}} v}\\ J_1 (X) =& \displaystyle{{1\over X}\ \int_0^{X} u J_0 (u)\ {\mathrm{d}} u}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-pupille/equation25.png)
L'amplitude diffractée dans une direction faisant un petit angle 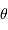 par rapport à l'axe optique, devient :
par rapport à l'axe optique, devient :
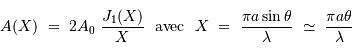
 Démonstration
Démonstration
Les calculs passent par les changements de variables
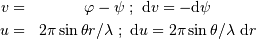
L'intensité diffractée dans la direction 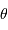 s'écrit donc :
s'écrit donc :
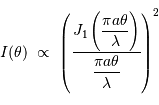
Zéros, anneaux et largeur à mi-hauteur
Pour 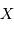 voisin de 0,
voisin de 0, 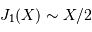 . Par ailleurs,
le premier zéro de la fonction
. Par ailleurs,
le premier zéro de la fonction 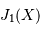 est pour
est pour 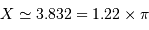 .
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille
.
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille 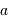 et de la longueur d'onde
et de la longueur d'onde 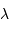 :
:
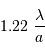
La figure de diffraction s'annule ensuite pour les rayons 2.23, 3.23, 4.24, 5.24.... en unité 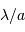 . Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
. Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...

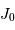 et
et 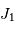 .
.

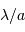 . Le premier zéro est à l'abscisse 1.22.
. Le premier zéro est à l'abscisse 1.22.
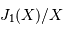 , avec
, avec 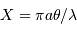 , avec
, avec 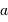 le diamètre de la pupille,
le diamètre de la pupille, 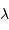 la longueur d'onde et
la longueur d'onde et 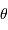 la direction d'observation.
la direction d'observation.
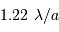 qui dimensionne la tache de diffraction.
qui dimensionne la tache de diffraction.
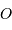 , et l'on note
, et l'on note 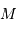 un point de la pupille. Cette pupille est éclairée par une onde plane uniforme, monochromatique, en incidence normale. L'amplitude de l'onde diffractée dans une direction repérée par le vecteur directeur
un point de la pupille. Cette pupille est éclairée par une onde plane uniforme, monochromatique, en incidence normale. L'amplitude de l'onde diffractée dans une direction repérée par le vecteur directeur 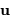 s'écrit :
s'écrit :
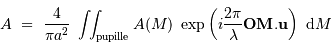

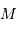 est un point courant de la pupille, de coordonnées polaires
est un point courant de la pupille, de coordonnées polaires 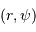 , et
, et 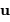 porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
porte la direction pour laquelle on recherche l'amplitude de l'onde diffractée.
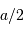 , il est préférable de décrire les coordonnées du point
, il est préférable de décrire les coordonnées du point 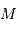 et de la direction de diffraction
et de la direction de diffraction 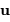 en coordonnées polaires, avec les notations suivantes :
en coordonnées polaires, avec les notations suivantes :
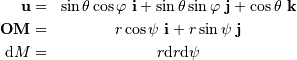
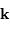 est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction
est le vecteur normal au plan de la pupille).
L'amplitude de l'onde diffractée dans la direction 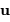 faisant un angle
faisant un angle 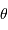 avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
avec l'axe optique s'écrit alors, en supposant l'amplitude incidente uniforme :
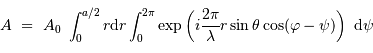
![\begin{eqnarray*} J_0 (X) =& \displaystyle{{1\over 2\pi} \int_0^{2\pi} \exp \bigl[-iX \cos v \bigr]\ {\mathrm{d}} v}\\ J_1 (X) =& \displaystyle{{1\over X}\ \int_0^{X} u J_0 (u)\ {\mathrm{d}} u}\\ \end{eqnarray*}](../pages_rayon/equations_diffraction-pupille/equation25.png)
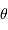 par rapport à l'axe optique, devient :
par rapport à l'axe optique, devient :
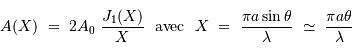
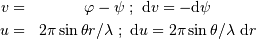
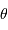 s'écrit donc :
s'écrit donc :
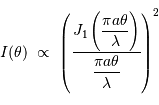
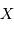 voisin de 0,
voisin de 0, 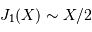 . Par ailleurs,
le premier zéro de la fonction
. Par ailleurs,
le premier zéro de la fonction 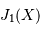 est pour
est pour 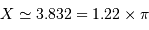 .
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille
.
La largeur à mi-hauteur du pic central de diffraction, supposée égale à la demi-largeur entre les 2 zéros de part et d'autre du pic central, s'écrit en fonction du diamètre de la pupille 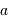 et de la longueur d'onde
et de la longueur d'onde 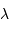 :
:
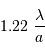
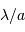 . Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...
. Les anneaux lumineux ont comme rayon, dans la même unité : 1.63, 2.68, 3.70, 4.71, 5.71...