L'agitation thermique des particules constituant un corps produit un rayonnement continu, dans tout le spectre électromagnétique. Ce rayonnement thermique est décrit par la loi du corps noir (absorbant parfait).
Le Soleil, comme la plupart des étoiles, rayonne comme un corps noir. La loi fondamentale, la loi de Planck, donne l'intensité (autrement appelée luminance) en fonction de la longueur d'onde :
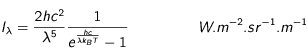
avec :
h la constante de Planck (h=6,6 10-34 J.s), c la vitesse de la lumière (c=3 108 m.s-1) et 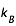 la constante de Boltzman (
la constante de Boltzman (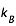 =1,38 10-23 J.K-1)
=1,38 10-23 J.K-1)
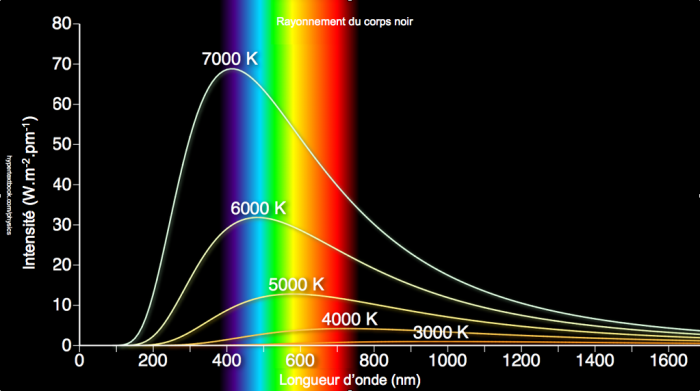
L'intensité décrit donc la puissance rayonnée par unité de surface, d'angle solide et de longueur d'onde. La figure ci-contre montre la courbe d'intensité pour des étoiles de température différente en fonction de la longueur d'onde. Deux points sautent aux yeux :
- Le maximum de l'intensité est d'autant plus élevé que la température de surface de l'étoile est grande
- La longueur d'onde du pic de maximum d'intensité se décale vers les petites longueurs d'onde (vers le bleu) avec l'augmentation de la température de surface de l'étoile
Ces deux remarques sont exprimées par deux lois lois simplifiées déduites de la loi de Planck.
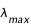 à la température de surfaceT :
à la température de surfaceT :
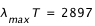 μm.K
μm.K

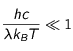
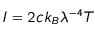
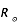 = 7 x 108 m
= 7 x 108 m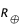 = 6,3 x 106 m
= 6,3 x 106 m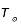 sachant que son pic d'émission (
sachant que son pic d'émission (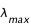 ) se situe à 500 nm. Même question pour la Terre
) se situe à 500 nm. Même question pour la Terre 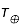 (
( 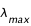 = 9,6 μm).
= 9,6 μm).
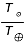 .
.
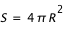 (avec R le rayon de la sphère).
(avec R le rayon de la sphère).