Récurrences des éclipses de Soleil
Auteur: P. Rocher - IMCCE - Observatoire de Paris
- Introduction
- Les périodes de récurrences des éclipses
- Introduction
- Les périodes de récurrence
- Périodes de récurrence-2
- Périodes de récurrence-3
- Périodes de récurrence-4
- En savoir plus: Décomposition d'un réel en fractions continues
- En savoir plus: Décomposition d'un réel en fractions continues-2
- En savoir plus: Autres périodes de récurrence
- En savoir plus: Autres périodes de récurrence-2
- L'origine du nom "saros"
- L'origine du nom "saros"-2
- Nombre d'éclipses dans un saros
- Les suites longues d'éclipses
- Introduction
- Eclipses homologues et suites longues
- Eclipses homologues et suites longues-2
- Eclipses homologues et suites longues-3
- Eclipses homologues et suites longues-4
- Evolutions des éclipses homologues
- Evolutions des éclipses homologues
- En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues
- En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues-2
- Evolutions des éclipses homologues - suite
- Evolutions des éclipses homologues - suite2
- En savoir plus: Exemple de saros, exemple de suite longue
- En savoir plus: Exemple de saros-2
- Les éclipses anciennes
- Introduction
- Le ralentissement de la Terre
- Les échelles de temps
- L'usage des éclipses anciennes
- Les sources anciennes
- Les sources anciennes-2
- Exemple de la détermination du ralentissement de la rotation terrestre
- La prédiction des éclipses
- Intérêt scientifique des éclipses de Soleil
- Intérêt scientifique des éclipses de Soleil-2
Introduction
 Introduction
Introduction
Ce chapitre est le plus complexe des chapitres sur les éclipses. Dans ce chapitre nous étudions les périodes de récurrence des éclipses de Soleil. Nous voyons qu'il existe plusieurs périodes de récurrence, notamment le Saros. Nous expliquons pourquoi cette période est réellement une bonne période de récurrence en analysant les principales perturbations lunaires et en introduisant la notion de révolution anomalistique. Nous définissons ensuite les suites d'éclipses séparées par cette période de temps. Ce sont des séries longues de Saros. Nous commentons et expliquons leur évolution : évolution des types d'éclipses, évolution des magnitudes, évolution des zones de visibilité sur Terre.
Enfin nous étudions les éclipses anciennes et leur utilisation pour déterminer le ralentissement de la révolution terrestre.
 Prérequis
Prérequis
Les périodes de récurrences des éclipses
Introduction
 Introduction
Introduction
Cette partie est le plus complexe des chapitres sur les éclipses. Dans cette partie du cours nous étudions les périodes de récurrence des éclipses de Soleil. Nous voyons qu'il existe plusieurs périodes de récurrence, notamment le Saros. Nous expliquons pourquoi cette période est réellement une bonne période de récurrence en analysant les principales perturbations lunaires et en introduisant la notion de révolution anomalistique. Nous définissons ensuite les suites d'éclipses séparées par cette période de temps. Ce sont des séries longues de Saros. Nous commentons et expliquons leur évolution : évolution des types d'éclipses, évolution des magnitudes, évolution des zones de visibilité sur Terre.
Enfin nous étudions les éclipses anciennes et leur utilisation pour déterminer le ralentissement de la révolution terrestre.
Dans cette première section, nous définissons les périodes de révolutions qui permettent de trouver les périodes de récurrence des éclipses de Soleil. Nous introduisons la notion de Saros. La partie "pour en savoir plus" décrit la méthode de décomposition d'un réel en fractions continues et comment l'on retrouve la période du Saros, elle donne également d'autres périodes de récurrence connues sous le nom de Saros chinois. Nous donnons ensuite l'origine du terme erroné de Saros et les caractéristiques des éclipses contenues dans une séries de Saros.
Les périodes de récurrence
Nous avons vu que les éclipses de Soleil et de Lune se produisent lorsque les syzygies (la conjonction et l'opposition de la Lune) ont lieu avec le soleil apparent au voisinage de la direction de la ligne des nœuds de l'orbite lunaire. Le retour d'une même phase lunaire est lié à la révolution synodique « L » (29,5305888532 jours) de la Lune. Le retour du Soleil dans la direction de la ligne des nœuds au moment des syzygies est équivalent au retour de la Lune près de ses nœuds, ce retour est lié à la révolution draconitique « G » (27,212220817 jours) de la Lune. Une période de récurrence des éclipses doit donc être un multiple commun à ces deux périodes.
On doit donc déterminer deux nombres x et y tel que x.G=y.L ou encore tel que x/y=L/G.
Les valeurs possibles pour x et y se calculent en utilisant la méthode de décomposition des réels en fractions continues.
Périodes de récurrence-2
Le rapport L/G est égal à 1,085195841, il s'écrit sous forme réduite : (1;11,1,2,1,4,3,5,1).
Ce qui donne pour x et y les solutions suivantes :
| x |
1 |
12 |
13 |
38 |
51 |
242 |
777 |
4127 |
| y |
1 |
11 |
12 |
35 |
47 |
223 |
716 |
3803 |
Le cycle correspondant à la solution 242/223, soit 223 lunaisons, est connu à tort sous le nom de saros. 223 lunaisons sont égales à 6585,321314 jours et 242 révolutions draconitiques sont égales à 6585,357436 jours, la différence 242L - 223L est de 0,03612 jour, soit 52 minutes.
On exprime parfois cette période en années et en jours, mais cela n'est pas recommandé, car 6 585 jours donnent 18 ans, plus 10 ou 11 ou 12 jours, cela dépend du nombre d'années bissextiles comprises dans les 18 années (5,4 ou 3), il est préférable de garder cette expression en jours.
Périodes de récurrence-3
Pourquoi le saros est une période de récurrence ?
La principale inégalité dans la longitude de la Lune, l'équation du centre, est fonction de sa distance angulaire au périgée de son orbite, cette distance angulaire porte le nom d'anomalie. L'intervalle de temps qui sépare en moyenne le passage de la Lune par la direction de son périgée, s'appelle la révolution anomalistique. Sa valeur moyenne est A = 27,554549878 jours. Il est très important de constater que le saros est également un multiple de cette révolution anomalistique, ainsi après un saros, non seulement on retrouve la même configuration Soleil Terre Lune mais la plus grosse inégalité dans la longitude de la Lune a presque la même valeur, donc on retrouve pratiquement le même écart entre la Lune vraie et la Lune moyenne. C'est principalement pour cette raison que le saros est une période de récurrence des éclipses. En effet le saros est construit à partir des révolutions synodique et draconitique moyennes de la Lune. Or l'écart entre la révolution synodique vraie et la révolution synodique moyenne de la Lune peut atteindre plus ou moins sept heures, or en sept heures la position de la Lune varie en moyenne de 3,5° en longitude (si l'on tient compte des perturbations cet écart peut atteindre 7,5°). Or comme les diamètres apparents de la Lune et du Soleil sont de l'ordre du demi-degré, il est totalement impossible de prédire une éclipse du Soleil uniquement avec la connaissance de la révolution synodique moyenne, seule la connaissance de la lunaison vraie permet cette prédiction. Donc si une période de récurrence utilise les révolutions synodique et draconitique moyennes, il faut également que cette période ramène la Lune vraie au même endroit par rapport à la Lune moyenne, donc que la période de récurrence soit aussi un multiple de la période de la plus grosse inégalité dans la longitude de la Lune.
On a 239 A = 6585,537419 jours et 1 saros = 239 A - 0,0079 A, au bout d'un saros, la Lune se retrouve donc à 2,8° en amont sur sa position orbitale.
Périodes de récurrence-4
Le saros ramène également le Soleil près des noeuds, il doit donc être aussi un multiple de l'année des éclipses E (346,62 jours) et l'on a bien 19 E = 6585,78 jours, l'écart avec le saros n'est que de 0,46 jour. Cette condition, moins stricte que le retour de la Lune à son noeud entraîne une légère évolution des éclipses d'un saros à l'autre.
Les inégalités dans le mouvement du soleil apparent sont également fonction de sa position angulaire par rapport à son périgée (périhélie de la Terre), cet angle porte le nom d'anomalie. La période de révolution qui ramène le soleil apparent à son périgée (ou la Terre à son périhélie), s'appelle révolution anomalistique ou année anomalistique et elle est égale à : a = 365,2596 jours.
Or 18 a = 6574,67 jours, l'écart avec le saros est de 10,65 jours, donc au bout d'un saros le soleil apparent ne s'est déplacé que de 10° sur son orbite par rapport à sa position un saros plus tôt, ce qui correspond à un décalage de 10° vers l'est parmi les constellations zodiacales.
En savoir plus: Décomposition d'un réel en fractions continues
 En savoir plus
En savoir plus
La décomposition d'un réel en fractions continues a été créée par Laplace en 1768, son but était d'obtenir une approximation d'un réel positif r sous la forme d'un quotient de deux entiers. La méthode consiste à décomposer le réel en partie entière et en partie décimale : r = a0 + u1, u1 étant inférieur à 1, on prend son inverse et on continue comme précédemment en itérant avec les restes successifs :
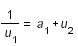
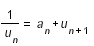
En remplaçant les ui par leurs expressions, le réel se présente sous la forme de fractions emboîtées qui forme la fraction continue :
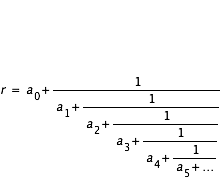
En savoir plus: Décomposition d'un réel en fractions continues-2
 En savoir plus
En savoir plus
On obtient des approximations successives de r au moyen de rapports d'entiers en tronquant le développement de la fraction à des ordres plus ou moins élevés que l'on appelle les réduites d'ordre n :
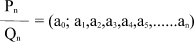
On passe de l'ordre n et n-1 à l'ordre n+1 par la relation de récurrence du second ordre suivante :
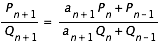
Ces formules de récurrence permettant ce calcul furent découvertes par le mathématicien Indien Bhascara II au début du XIIIe siècle, soit 5 siècles avant que le mathématicien Anglais John Wallis ne les redécouvre en Europe.
 Exemple
Exemple
représentation du nombre 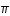
On a 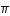 = 3,141592654
= 3,141592654
Sa forme réduite d'ordre 4 s'écrit : (3;7,15,1,293)
Les approximations successives sont : 3, 22/7, 333/106, 355/113, 104348/33215.
En savoir plus: Autres périodes de récurrence
 En savoir plus
En savoir plus
Comme nous venons de le voir, pour qu'une période soit une période de récurrence des éclipses, il faut non seulement qu'elle soit un multiple des révolutions synodique (L) et draconitique (G) de la Lune, mais il faut également qu'elle soit un multiple de la révolution anomalistique (A) de la Lune. On doit donc trouver trois nombres x, y et z tels que x.L ~ y.G ~ z.A. Le tableau suivant donne une série de solutions.
| jours |
x |
y |
z |
Durée (ans) |
| |
223 |
242 |
239 |
18,03 |
| 6585+ |
0,321 |
0,357 |
0,537 |
|
| |
2148 |
2331 |
2302 |
173,7 |
| 63430+ |
1,705 |
1,684 |
0,574 |
|
| |
2371 |
2573 |
2541 |
191,7 |
| 70016+ |
1,026 |
1,042 |
0,112 |
|
La première ligne correspond au saros, les deux solutions suivantes ramènent bien la lunaison et la Lune près de son noeud, mais décalent beaucoup plus la Lune par rapport à son périgée (14,8° pour la seconde et 11,9° pour la troisième). Elles sont donc moins stables que le saros.
En savoir plus: Autres périodes de récurrence-2
 En savoir plus
En savoir plus
On peut également chercher des solutions sous la forme x.L ~ 2.y.G/2 ~ z.A. Ces solutions font intervenir la demi-révolution draconitique, cela correspond donc à des récurrences avec alternance de noeud. Le tableau suivant donne une série de solutions.
| jours |
x |
y |
z |
Durée (ans) |
| |
135 |
146,5 |
145 |
10,92 |
| 3986+ |
0,629 |
0,590 |
9,41 |
|
| |
1074 |
1165,5 |
1151 |
86,83 |
| 31715+ |
0,852 |
0,842 |
0,287 |
|
| |
1297 |
1407,5 |
1390 |
104,86 |
| 38300+ |
1,174 |
1,199 |
0,824 |
|
La première solution que l'on appelle «saros chinois» car elle était connue des chinois, n'est pas très stable à cause de l'écart en anomalie. La seconde et la dernière solution sont meilleures car les écarts en anomalie sont beaucoup plus faibles.
Ainsi pour la seconde solution : 1074.L - 1165,5.G = 0,009 jour = 13 minutes et 1074.L - 1151.A = 0,56 jour, au bout d'un cycle, la Lune se retrouve à 7,4° en aval sur sa position orbitale.
Et pour la dernière solution : 1297.L - 1407,5.G = -0,027 jour = -39 minutes et 1297.L - 1390.A = 0,35 jour, au bout d'un cycle, la Lune se retrouve à 4,5° en aval sur sa position orbitale.
L'origine du nom "saros"
Edmont Halley (1656 - 1742) publia en 1961 dans les Philosophical Transactions un mémoire dans lequel il proposait de corriger un passage de l'Histoire naturelle de Pline l'Ancien (23 - 79 ap. J.-C.) où il était question de la période de récurrence des éclipses (Histoire Naturelle, II, 56). Le texte est le suivant : " Il est sûr que les éclipses se reproduisent dans le même ordre au bout de 222 mois ". Sur d'autres manuscrits on trouve les valeurs de 213 et 293 mois. Halley corrige à juste titre la valeur de 222 mois en 223 mois.
En consultant une encyclopédie byzantine du Xe siècle, la Souda, il trouva la mention du mot saros dans le texte suivant " Saros, mesure et nombre chez les Chaldéens. Un saros contient 222 mois lunaires qui font 18 ans et 6 mois. 120 saros correspondent à 2222 années ". Croyant à tort que la Souda dépendait ici de Pline, Halley en conclut que les Chaldéens appelaient saros la période de 223 ans de Pline.
Le terme sar en sumérien a le sens d'univers, et en temps que nombre, il représente la quantité 3600. Dans le sens de 3 600 ans le terme saros est utilisé par Berossos (~290 avant J.-C.) et après lui par Abydenus (deux siècles avant J.-C.) puis par Synkellos en l'an 800 après J.-C.
L'origine du nom "saros"-2
La Souda nomme saros une période de 222 mois lunaires et dit explicitement qu'elle correspond à 18 ans et 6 mois avec une année de 12 mois lunaires. La période portant le nom de saros chez les Chaldéens n'a donc rien à voir avec les éclipses.
L'erreur de Halley a été dénoncée par l'astronome Guillaume Le Gentil de La Galaisière (1725 - 1792) dans deux articles très critiques publiés en 1756, alors que Montucla refait l'erreur d'Halley dans son Histoire des mathématiques (1758). D'autres astronomes et historiens essaieront en vain de corriger l'erreur d'Halley : Ideler en 1825, Tannery en 1893, Schiaparelli en 1908, Bigourdan en 1911 et Pannekoek en 1917.
Cette erreur sera amplifiée par la légende de Thalès de Milet (VIe siècle avant J.-C.) rapportait par Hérodote (484 à 425 avant J.-C.) dans l'Enquête (p. 174) Thalès avait prédit aux Ioniens un obscurcissement du Soleil " pour l'année dans laquelle elle se produisit ". Cette éclipse aurait permis de mettre fin à une guerre entre les Mèdes et les Lydiens.
Nombre d'éclipses dans un saros
Le saros comporte 38 saisons d'éclipses, revenant en moyenne toutes les 5 ou 6 lunaisons. À chaque saison d'éclipses il y a au moins deux éclipses et parfois trois éclipses. En moyenne un saros comprend 84 éclipses, réparties en 42 éclipses de Soleil et 42 éclipses de Lune.
Les 42 éclipses de Lune se répartissent de la manière suivante : 14 éclipses par la pénombre, 28 éclipses par l'ombre dont 14 éclipses partielles et 14 éclipses totales.
Les 42 éclipses de Soleil se répartissent de la manière suivante : 14 éclipses partielles et 28 éclipses centrales.
Ce nombre d'éclipses par saros est une valeur moyenne, en réalité il existe des saros riches pouvant atteindre jusqu'à 94 éclipses (47 de chaque) et des saros pauvres comportant 78 éclipses.
Les canons d'éclipses construits à l'IMCCE comportent 28512 éclipses sur une période de 5999 ans, soit en moyenne 4,7528 éclipses par an et 85,7 éclipses par saros (valeur que l'on peut arrondir à 86). Cette valeur est légèrement plus forte que la valeur moyenne (84). On retrouve le saros moyen du canon d'Oppolzer, construit sur une période plus courte, qui est de 86 éclipses.
Les suites longues d'éclipses
Introduction
 Introduction
Introduction
Dans cette section nous définissons la notion de suite longues d'éclipses de Soleil liée au Saros. Nous regardons comment évoluent les éclipses qui se succèdent dans ces suites. Nous traitons dans la partie pour en savoir plus, l'évolution géographique des éclipses des suites longues à la surface du globe terrestre et nous donnons les limites de prédiction locale à partir de la connaissance du Saros. En fin de section nous donnons et commentons un exemple de série longue.
Eclipses homologues et suites longues
Nous avons vu qu'il existe une période de récurrence des éclipses, le saros, qui ramène sensiblement la même éclipse après une période de 6585,32 jours. Ces éclipses séparées par un saros sont appelées éclipses homologues. En réalité, elles ne sont pas parfaitement identiques, mais elles évoluent légèrement d'un saros à l'autre et elles forment des suites qui portent sur de grandes périodes de temps d'où leur nom de suites longues.
Eclipses homologues et suites longues-2
Evolution de la longitude de la conjonction après un saros
Nous allons regarder comment évolue la longitude de la conjonction après une période d'un saros. L'écart entre le saros de 223 lunaisons « L » et les 242 révolutions draconitiques « G » est de moins 52 minutes de temps (- 0,03612 jour).
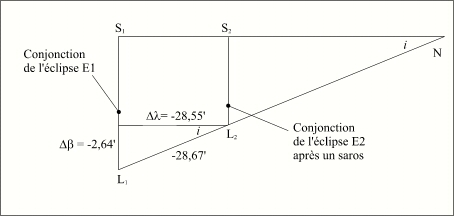
Crédit : IMCCE/Patrick Rocher
Durant ces 52 minutes la Lune, sur son orbite, se déplace en moyenne par rapport à son noeud de -0,03612 x 360°/G = -28,67'. La Lune en conjonction se trouve donc déplacée sur son orbite de 28,67' dans le sens rétrograde par rapport au noeud. Compte tenu de l'inclinaison de l'orbite lunaire, ce décalage se traduit par un décalage de la longitude céleste Δ
λ = -28,55' et par une variation de la latitude céleste de la Lune de Δ
β = -2,64'.
Eclipses homologues et suites longues-3
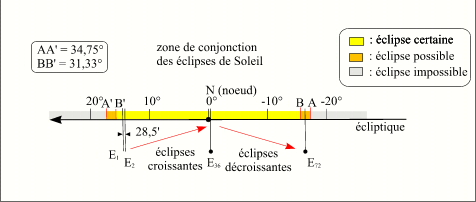
Crédit : IMCCE/Patrick Rocher
Les conjonctions des éclipses homologues vont donc parcourir l'arc BB' dans le sens rétrograde avec un pas moyen de 28,55'. Si l'on divise l'arc BB' par 28,55', on constate qu'il peut contenir 66 éclipses et si l'on divise l'arc AA' par 28,55' on voit qu'il peut contenir 74 éclipses. Ces séries d'éclipses sont appelées suites longues. L'étude des canons d'éclipses montre qu'en moyenne ces suites comportent 72 éclipses. Ce qui correspond à une période de temps d'environ 1300 ans.
Eclipses homologues et suites longues-4
Aspects des éclipses d'une suite longue
Les premières éclipses d'une suite longue sont faibles, car elles sont proches de l'arc A'B', donc loin du noeud. Ensuite, leur grandeur va croître jusqu'à ce qu'elles se produisent au voisinage du noeud, puis leur grandeur va décroître pour finir de nouveau faible au voisinage de l'arc BA. Pour une suite longue de 72 éclipses, si l'on respecte les pourcentages des éclipses partielles et des éclipses centrales (1/3 et 2/3), on aura donc successivement 12 éclipses partielles de grandeur croissante (sur 200 ans), puis 24 éclipses centrales de grandeur croissante (sur 450 ans), puis 24 éclipses centrales de grandeur décroissante (sur 240 ans) et enfin 12 éclipses partielles de grandeur décroissante (sur 200 ans). Dans la pratique, les deux ou trois éclipses du milieu de la suite longue sont maximales, elles servent de transition entre la période de croissance et de décroissance des éclipses. On remarque que toutes les éclipses d'une suite ont lieu au même noeud. Si la suite longue a lieu au noeud descendant les latitudes célestes successives de la Lune croissent des latitudes négatives aux latitudes positives, l'ombre et la pénombre vont donc se déplacer sur la Terre du sud au nord. Inversement pour une suite longue au noeud ascendant les latitudes célestes successives de la Lune décroissent des latitudes positives aux latitudes négatives, l'ombre et la pénombre vont donc se déplacer sur la Terre du nord au sud.
Evolutions des éclipses homologues
Evolution en longitude terrestre
Nous avons vu que la période du saros n'est pas un nombre entier de jours, sa valeur est de 6585,32 jours. Donc entre deux éclipses homologues, la Terre n'a pas tourné d'un nombre entier de jour, les zones concernées par les éclipses ne sont donc pas les mêmes. En 0,32 jour la Terre tourne d'environ 120°, les zones concernées par l'éclipse se déplacent donc d'environ 120° vers l'ouest. Ce décalage est bien visible sur la carte ci-contre, où nous avons tracé les lignes de centralité des éclipses homologues à l'éclipse du 11 août 1999.
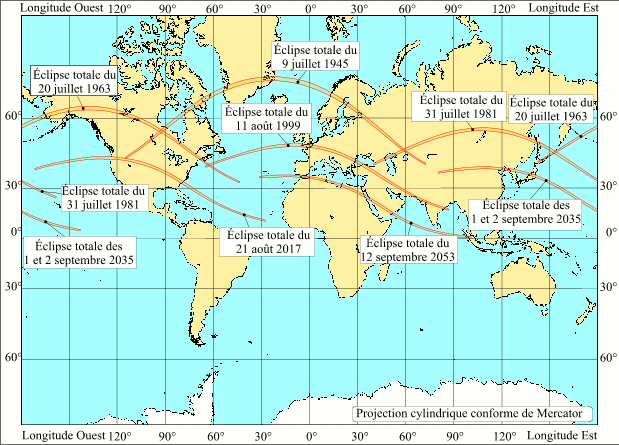
Sept éclipses homologues de la suite longue contenant l'éclipse du 11 août 1999
Crédit : IMCCE/Patrick Rocher
Evolutions des éclipses homologues
Evolution en latitude terrestre
Nous avons vu que les suites longues au noeud ascendant parcourent la Terre du nord au sud et que les suites longues au noeud descendant parcourent la Terre du sud au nord. Le décalage en latitude terrestre provient du décalage en latitude céleste de la Lune d'une éclipse homologue à l'autre. Un décalage en latitude céleste Δβ de la Lune, même si le sens du décalage est conservé, ne se traduit pas directement par un même décalage de l'ombre en latitude terrestre. En effet, les latitudes célestes sont comptées à partir de l'écliptique et les latitudes terrestres sont comptées à partir de l'équateur terrestre, on doit donc tenir compte de l'obliquité de l'écliptique sur l'équateur terrestre, ainsi les variations de latitude céleste sont inclinées d'environ 23° par rapport au méridien terrestre. De plus la variation de latitude doit être projetée sur une sphère et la projection sur la sphère terrestre produit un décalage plus important près des pôles. Sur la figure ci-contre, Δβ représente la variation de latitude céleste de la Lune, à cette variation correspond une variation Δr sur l'axe normal à l'écliptique (pôle de l'écliptique) et une variation Δl sur la sphère terrestre, cette variation a deux composantes, une composante Δλ en longitude terrestre, qui produit le léger décalage en longitude vers l'est, et une composante en latitude terrestre Δϕ.
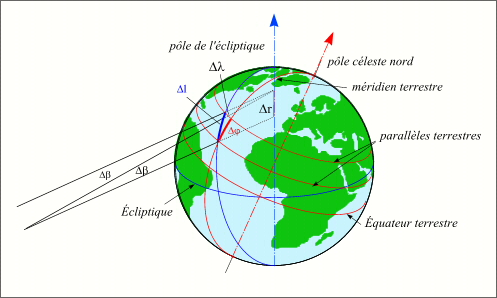
Variation de la latitude terrestre
Crédit : IMCCE/Patrick Rocher
Cela explique qu'après une période de trois saros (ou Exeligmos) les lignes de centralité ne sont pas alignées en longitude, comme on pourrait si attendre après trois décalages de 120° en longitude, mais sont décalées légèrement vers l'est comme on le constate sur la carte des éclipses homologues à l'éclipse du 11 août 1999.
En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues
 En savoir plus
En savoir plus
Nous allons essayer de quantifier un peu mieux les décalages en latitude. En moyenne, au bout de trois saros les lignes de centralité des éclipses se décalent d'environ 900 km dans le plan passant par la Terre et normal à l'axe des cônes (plan de Bessel), elles parcourent donc la Terre en environ 45 saros. On retrouve approximativement le nombre d'éclipses centrales dans une suite longue (48).
Mais il convient de noter que la variation en latitude des séries homologues ne se fait pas toujours de façon uniforme d'un pôle à l'autre. Elle peut être momentanément inversée ou accélérée. Prenons le cas d'une suite longue au noeud ascendant, les lignes de centralité parcourent la sphère terrestre du nord au sud. Après trois saros la ligne de centralité descend d'environ 900km ce qui correspond à une variation de la latitude de la Lune de 7,92' (3 x 2,64'). Or dans ce mouvement nous n'avons considéré que le déplacement en latitude de la Lune, le Soleil étant toujours dans l'écliptique.
En savoir plus: Evolution réelle des lignes de centralité des éclipses homologues-2
 En savoir plus
En savoir plus
En réalité comme l'écliptique est incliné de 23° par rapport à l'équateur terrestre, nous devons également tenir compte des variations des hauteurs du Soleil par rapport à l'équateur terrestre, donc des variations de déclinaison du Soleil, or ces variations peuvent être très grandes par rapport aux variations en latitude de la Lune. Ainsi trois saros font environ 54 ans et 34 jours, donc au bout de trois saros le Soleil se retrouve décalé d'environ 34° sur l'écliptique, cette variation de 34° sur l'écliptique, si elle est répartie de part et d'autre d'un équinoxe peut se traduire par des variations en déclinaison de plus au moins 13°, ce qui correspond à une variation de hauteur de 13° du Soleil dans le méridien, à midi, c'est-à-dire une descente (si on est de part et d'autre de l'équinoxe de d'automne) ou une remontée (si on est de part et d'autre de l'équinoxe printemps) de 1440 km environ. Une descente du Soleil en déclinaison fait remonter l'ombre donc la ligne de centralité et une montée du Soleil fait redescendre l'ombre donc la ligne de centralité. Ainsi dans une série longue, lorsque les dates des séries homologues séparées par trois saros se trouvent distribuées autour des équinoxes, les latitudes de la bande de centralité peuvent être accentuées de 1440 km (1440+900 = 2340 km) ou diminuées de 1440km (900-1440 = -540 km). Ce phénomène est localisé dans le temps et disparaît lorsqu'on s'éloigne des dates des équinoxes.
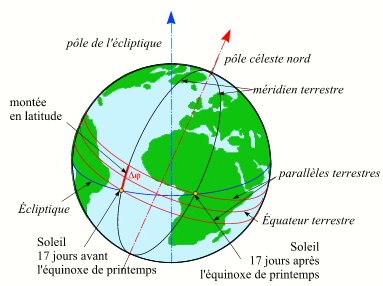
Variation de la hauteur du Soleil au méridien de part et d'autre des équinoxes
Crédit : IMCCE/Patrick Rocher
Evolutions des éclipses homologues - suite
Variation sur le fond d'étoile et dans l'année
Nous rappelons que d'un saros à l'autre, le Soleil, donc l'éclipse se décale d'environ 10,5° par rapport aux constellations zodiacales. Au cours d'une suite longue le soleil apparent effectue plus de deux tours complets d'orbite et l'on rencontre toutes les configurations liées au soleil apparent. Les éclipses parcourent les quatre saisons et cela deux fois.
Variation des types d'éclipses
Nous avons vu également que suite à l'écart entre un saros et 239 révolutions anomalistiques, la distance de la Lune à son périgée varie de 2,8° d'un saros à l'autre. Au cours d'une suite longue de 72 saros, les conjonctions lunaires liées aux éclipses homologues (donc la Lune) ne vont parcourir que 202° de l'orbite lunaire, soit un peu plus que la moitié. De plus durant les 48 éclipses centrales du saros, cet arc se réduit à 134°, il convient de comparer cette valeur avec les portions de l'orbite lunaire où les éclipses sont totales ou annulaires.
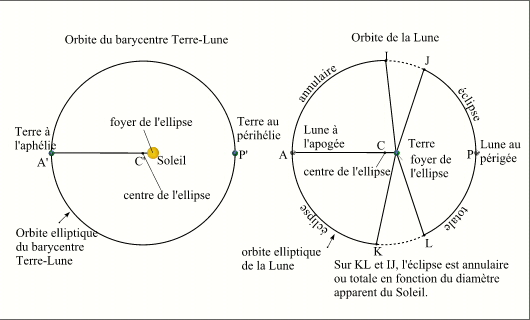
Orbites de la Terre et de la Lune
Crédit : IMCCE/Patrick Rocher
Ainsi si le périgée est proche du milieu de cet arc de 134°, la suite longue est trés riche en éclipses totales, si au contraire, cet arc avoisine l'apogée la suite longue est trés riche en éclipses annulaires.
Evolutions des éclipses homologues - suite2
Remarques supplémentaires
Il ne faut jamais perdre de vue que toutes les variations dans les suites longues sont calculées avec des valeurs moyennes et ne sont jamais toute à fait conformes avec la réalité. Ainsi le décalage de la conjonction par rapport au noeud de 28,55' est une valeur moyenne. En réalité, le Soleil avance plus vite en janvier (il est proche du périgée) qu'en juillet (proche de l'apogée), le calcul montre que la variation de la longitude de la conjonction par rapport au noeud est de l'ordre de 6' en janvier (au lieu de 28,55') et qu'elle atteint 48' en juillet. Les éclipses homologues d'hiver sont donc plus semblables que les éclipses homologues d'été qui évoluent sensiblement plus vite.
Il est facile de connaître la position d'une éclipse dans une suite longue d'éclipses. Les éclipses croissantes ont toujours lieu après le passage au noeud et les éclipses décroissantes ont toujours lieu avant le passage au noeud. La connaissance des instants des syzygies et du passage au noeud permet donc de positionner l'éclipse dans sa suite longue. Inversement la connaissance de la position d'une éclipse dans sa suite longue permet, sauf pour l'éclipse maximale, de savoir sa position par rapport aux noeuds. De plus dans le cas d'un doublet d'éclipses (Lune Soleil ou Soleil Lune) la première éclipse, qui a lieu avant le passage au noeud appartient à la partie décroissante de sa suite longue et la seconde éclipse appartient à la partie croissante de sa suite longue. Dans le cas d'un triplet d'éclipses, la première appartient à la fin de la partie décroissante de la suite longue qui la contient, la dernière appartient au début de la partie croissante de la suite longue qui la contient et l'éclipse médiane se trouve au voisinage du maximum de sa suite longue.
En savoir plus: Exemple de saros, exemple de suite longue
 En savoir plus
En savoir plus
Le tableau suivant donne la liste des éclipses de la suite longue contenant l'éclipse du 31 mai 2003. On donne successivement le numéro de l'éclipse dans la suite longue, le type d'éclipse, la date de l'éclipse, sa magnitude et la durée maximale de la phase centrale lorsque cette phase existe.
| n° type |
date |
magnitude |
durée |
| 1P |
12/101624 |
0.0085968 |
|
| 2P |
23/10/1642 |
0.0548679 |
|
| 3P |
03/11/1660 |
0.0896182 |
|
| 4P |
14/11/1678 |
0.1146153 |
|
| 5P |
24/11/1696 |
0.1316624 |
|
| 6P |
07/12/1714 |
0.1419092 |
|
| 7P |
17/12/1732 |
0.1469513 |
|
| 8P |
28/12/1750 |
0.1505860 |
|
| 9P |
08/01/1769 |
0.1530884 |
|
| 10P |
19/01/1787 |
0.1591577 |
|
| 11P |
30/01/1805 |
0.1675941 |
|
| 12P |
11/02/1823 |
0.1857746 |
|
| 13P |
21/02/1841 |
0.2097100 |
|
| 14P |
04/03/1859 |
0.2462690 |
|
| 15P |
15/03/1877 |
0.2919636 |
|
| 16P |
26/03/1895 |
0.3533467 |
|
| 17P |
06/04/1913 |
0.5110283 |
|
| 18P |
17/04/1931 - 18/04/1931 |
0.5110283 |
|
| 19P |
28/04/1949 |
0.6095708 |
|
| 20P |
09/05/1967 |
0.7205292 |
|
| 21P |
19/05/1985 |
0.8411277 |
|
| 22A |
31/05/2003 |
0.9696001 |
03m34.08s |
| 23A |
10/06/2021 |
0.9721316 |
03m47.99s |
| 24A |
21/06/2039 |
0.9730915 |
04M01.45S |
| 25A |
01/07/2057 - 02/07/2057 |
0.9737206 |
04m40.41s |
| 26A |
13/07/2075 |
0.9737206 |
04m40.41s |
| 27A |
23/07/2093 |
0.9735538 |
05m06.77s |
| 28A |
04/08/2111 |
0.9731384 |
05m36.78s |
| 29A |
14/08/2129 - 15/08/2129 |
0.9724857 |
06m09.32s |
| 30A |
26/08/2147 |
0.9716470 |
06m42.98s |
| 31A |
05/09/2165 |
0.9706588 |
07m15.78s |
| 32A |
16/09/2183 - 17/09/2183 |
0.9695596 |
07m46.87s |
| 33A |
28/09/2201 |
0.9684309 |
08m14.61s |
| 34A |
09/10/2219 |
0.9672517 |
08m39.72s |
| 35A |
19/10/2237 |
0.9661547 |
09m00.30s |
| 36A |
30/10/2255 - 31/10/2255 |
0.9651065 |
09m17.21s |
| 37A |
10/11/2273 |
0.9642541 |
09m28.20s |
| 38A |
21/11/2291 |
0.9635287 |
09m34.68s |
| 39A |
02/12/2309 - 03/12/2309 |
0.9630803 |
09m34.31s |
| 40A |
14/12/2327 |
0.9628599 |
09m28.43s |
| 41A |
24/12/2345 |
0.9629606 |
09m15.58s |
| 42A |
04/01/2364 -05/01/2364 |
0;9633421 |
08m57.77s |
| 43A |
15/01/2382 |
0.9640683 |
08m34.41s |
| 44A |
26/01/2400 |
0.9651082 |
08m07.46s |
| 45A |
05/02/2418 - 06/02/2418 |
0.9664621 |
07m37.67s |
| 46A |
17/02/2454 |
0.9681073 |
07m06.45s |
| 47A |
27/02/2454 |
0.9700297 |
06m34.42s |
| 48A |
09/03/2472 - 10/03/2472 |
0.9721718 |
06m02.57s |
| 49A |
21/03/2490 |
0.9745093 |
05m31.07s |
| 50A |
01/04/2508 |
0.9769654 |
05m00.43s |
| 51A |
12/04/2526 -13/04/2526 |
0.9795505 |
04m29.66s |
| 52A |
23/04/2544 |
0.9821258 |
03m59.66s |
| 53A |
04/05/2562 |
0.9847154 |
03m29.01s |
| 54A |
14/05/2580 - 15/05/2580 |
0.9871679 |
02m58.81s |
| 55A |
26/05/2598 |
0.9895234 |
02m27.78s |
| 56A |
06/06/2616 |
0.9916211 |
01m58.16s |
| 57A |
17/06/2634 |
0.9935042 |
01m29.84s |
| 58A |
27/06/2652 - 28/06/2652 |
0.9935042 |
01m29.84s |
| 59A |
09/07/26700.9961687 |
0.9961687 |
00m47.26s |
| 60A |
19/07/2688 |
0.9961687 |
00m47.26s |
| 61A |
31/07/2706 -01/08/2706 |
0.9960352 |
00m36.88s |
| 62P |
11/08/2724 |
0.8822576 |
|
| 63P |
22/08/2742 |
0.7560645 |
|
| 64P |
01/09/2760 |
0.6399250 |
|
| 65P |
13/09/2778 |
0.5318151 |
|
| 66P |
23/09/2796 |
0.4338706 |
|
| 67P |
04/10/2814 |
0.3469499 |
|
| 68P |
15/10/2832 |
0.2725393 |
|
| 69P |
26/10/2850 |
0.2098505 |
|
| 70P |
05/11/2868 |
0.1587829 |
|
| 71P |
17/11/2886 |
0.1194801 |
|
| 72P |
28/11/2904 |
0.0907818 |
|
| 73P |
09/12/2922 |
0.0696946 |
|
| 74P |
20/12/2940 |
0.0570489 |
|
| 75P |
31/12/2958 |
0.0487713 |
|
| 76P |
10/01/2977 |
0.0452276 |
|
| 77P |
22/01/2995 |
0.0403169 |
|
En savoir plus: Exemple de saros-2
 En savoir plus
En savoir plus
On remarque que cette suite n'est pas complète, en effet le canon d'éclipse de l'IMCCE s'arrête en 2999, il y a probablement des éclipses de la suite qui sont postérieures à cette date. Malgré cela on dépasse la valeur moyenne de 72 éclipses. Et l'on est assez loin des valeurs moyennes, ainsi le nombre d'éclipses partielles de la partie croissante est de 21, la moyenne donne 12 ! On constate également que toutes les éclipses centrales sont des éclipses annulaires, donc l'arc parcouru par les conjonctions lunaires est au voisinage de l'apogée. L'éclipse du 31 mai 2003 est la première éclipse centrale de la partie croissante de la suite, on peut donc en déduire qu'elle a lieu après le passage au noeud et relativement longtemps après ce passage. De plus elle est proche d'un des pôles terrestres. On ne peut pas savoir si la suite est au noeud ascendant ou descendant de l'orbite lunaire. Pour cela il suffit de connaître la latitude de la Lune à la conjonction pour une seule éclipse de la suite. Cette latitude est positive pour l'éclipse du 31 mai donc cette suite longue est au noeud ascendant et l'éclipse du 31 mai 2003 est proche du pôle nord terrestre et les éclipses de la suite vont parcourir le globe terrestre du nord au sud.
Les éphémérides de la Lune nous donnent les informations suivantes :
- le 28/05/2003 à 13h 04m 44s UT : la Lune à l'apogée (distance maximale à la Terre) d=406168 km, diamétre. apparent. =29.5'.
- le 30/05/2003 à 08h 32m 17s UT : la Lune passe par le noeud ascendant de son orbite, long. moyenne = +59° 30,9'.
- le 31/05/2003 à 04h 08m 18s UT : maximum de l'éclipse annulaire de Soleil.
- le 31/05/2003 à 04h 19m 51s UT : Nouvelle Lune.
On constate que le maximum de l'éclipse a bien lieu entre le passage et la conjonction, qu'il est proche de la conjonction (11m 33s) mais éloigné du passage au noeud (19h 36m 1s). L'éclipse est proche du passage de la Lune à l'apogée elle est donc annulaire.
Les éclipses anciennes
Introduction
 Introduction
Introduction
Cette section traite des éclipses anciennes de Soleil et explique comment on utilise ces éclipses pour déterminer le ralentissement de la révolution terrestre.
Nous donnons un historique des prédictions des éclipses anciennes et nous donnons les possibilités des prédictions au fur et à mesure que les connaissances de l'orbite lunaire et de la cartographie évoluent. Ces propos sont illustrés par les cartes des lignes de visibilité des éclipses anciennes calculées avec les théories actuelles.
Le ralentissement de la Terre
Aussitôt que les astronomes eurent à leur disposition des théories de la Lune et du Soleil suffisamment précises, ils essayèrent de calculer et de tracer les zones de visibilité des éclipses anciennes décrites dans les textes antiques. Ils trouvèrent bien les éclipses de Soleil aux bonnes dates, mais ils s'aperçurent que les zones de visibilité qu'ils calculaient ne correspondaient pas aux zones d'observation des l'éclipses. E. Halley en 1693, puis R. Dunthorne en 1749, avancèrent l'idée que la Lune n'était pas à sa bonne position. Pour rendre cohérents les calculs d'éclipses et les observations on introduisit une accélération séculaire dans la théorie de la longitude de la Lune. Par la suite les mécaniciens célestes essayèrent de trouver une explication théorique à ce phénomène. Mais ils trouvèrent des explications théoriques qui n'expliquaient qu'en partie la valeur de cette accélération. En 1866, W. Ferrel et Delaunay vont émettre l'hypothèse d'un ralentissement de la rotation terrestre sous l'effet des marées océaniques, ce ralentissement contrebalancerait l'accélération qui apparaît dans l'observation du mouvement de la Lune. Ce ralentissement fut mis en évidence par Spencer Jones en 1926 et 1939, mais il faudra attendre la deuxième moitié du XXe siècle pour que l'on considère le phénomène réciproque, à savoir, l'influence des marées océaniques sur l'orbite lunaire et que l'on définisse complètement le problème. En réalité, l'accélération séculaire observée dans le mouvement de la Lune est la combinaison de trois termes : une accélération séculaire gravitationnelle due aux perturbations planétaires, une accélération séculaire due aux marées océaniques et une accélération séculaire fictive due au ralentissement de la rotation terrestre. Cette dernière accélération disparaît lorsqu'on utilise une échelle de temps uniforme (non liée à la rotation de la Terre). L'accélération séculaire gravitationnelle se calcule à partir des perturbations planétaires, l'accélération séculaire due aux marées océaniques se calcule à partir des mesures lasers des distances Terre-Lune. Le ralentissement de la rotation terrestre se calcule grâce aux éclipses anciennes.
Les échelles de temps
La rotation de la Terre autour de son axe a été longtemps considérée comme uniforme et a fourni une échelle de temps unique, le Temps universel (UT ou TU). La mise en évidence du ralentissement de la rotation terrestre par Spencer Jones a rendu nécessaire l'introduction à partir de 1960 d'une nouvelle échelle de temps, le Temps des éphémérides (TE). Cette échelle de temps est fonction de la révolution de la Terre autour du Soleil, cette révolution est très stable et elle fournit une meilleure réalisation d'un temps uniforme. Depuis 1967, cette échelle de temps a été remplacée par une échelle encore plus stable le Temps atomique international (TAI). Le temps civil actuel est encore basé sur la rotation de la Terre, il porte le nom de Temps universel coordonné (UTC) et n'est donc pas un temps uniforme.
L'usage des éclipses anciennes
Les théories des corps du système solaire, utilisent comme argument du temps, une échelle de temps uniforme liée au Temps atomique international appelée Temps Terrestre (TT). Pour connaître la portion du globe terrestre concerné par une éclipse, il faut connaître l'écart entre cette échelle de temps (TT) et l'échelle de temps non uniforme liée à la rotation de la Terre, le Temps universel (TU). Inversement lors d'une éclipse ancienne, l'écart entre la zone de visibilité calculée avec le Temps terrestre uniforme et les lieux d'observations effectifs de l'éclipse nous donne une approximation de l'écart (TT-TU) entre les deux échelles de temps. Un travail très important, portant sur de très nombreuses éclipses de Lune et de Soleil allant de l'an 763 avant J.-C. jusqu'à nos jours a été réalisé par Richard Stephenson et a permis de modéliser, pour le passé, les écarts entre le Temps Terrestre et le Temps universel.
Les sources anciennes
Les éclipses anciennes, de Lune et de Soleil, proviennent de quatre sources principales : les Babyloniens de 700 avant J.-C. à 50 avant J.-C., les Chinois de 700 avant J.-C. à 1500 après J.-C., les Européens de 500 avant J.-C. à 1 600 après J.-C. et les Arabes de 800 après J.-C. à 1 300 après J.-C. Certaines sources, bien que remontant très loin dans le temps, n'ont été connues que très récemment. C'est le cas notamment des sources babyloniennes et assyriennes que l'on ne sait déchiffrer que depuis le milieu du XIXe siècle.
Un des premiers astronomes à répertorier les éclipses anciennes fut Claude Ptolémée (milieu du IIe siècle), à cette occasion il créa une chronologie, l'ère de Nabonassar (le vrai nom est Nabu-nasir) qui débute en l'an 747 avant J.-C. et qui utilise l'année vague égyptienne de 365 jours. Ptolémée cite dans l'Almageste 10 éclipses de Lune observées par les Babyloniens et aucune éclipse de Soleil, les plus vieilles éclipses de Lune datant de 721 et 720 avant J.-C. Toutes les autres éclipses de Soleil et de Lune observées par les Babyloniens ou les Assyriens proviennent de tablettes écrites en caractères cunéiformes.
Les sources anciennes-2
La datation exacte de ces éclipses anciennes n'était pas une chose facile à réaliser avant que l'on ne connaisse le ralentissement de la rotation terrestre. En effet pour les dates indiquées, les éclipses calculées ne passaient pas par les lieux d'observations. Par exemple dans le cas de l'éclipse dite de Thalès, éclipse qui selon la légende rapportée par Hérodote dans l'Enquête, aurait été prédite aux Ioniens par Thalès, les astronomes et les historiens ont longtemps hésité entre plusieurs dates. Ainsi Eusèbe et Cicéron la plaçait en -584 (585 avant J.-C.), Scaliger en -582 (583 avant J.-C.) et Arago en -609 (610 avant J.-C.) Les astronomes anglais Airy et Fotheringham hésitèrent entre l'éclipse du 17 mai -602 (603 avant J.-C.) et celle du 28 mai -584 (585 avant J.-C.) avec une préférence pour la deuxième date. De nos jours, la bonne connaissance de l'écart entre le TT et le TU nous permet de confirmer la deuxième date, l'éclipse de -584 passant sur l'Asie Mineure.
La figure ci-contre nous montre les tracés des bandes de centralité des éclipses du 24 mai -584 et du 18 mai -602, nous avons tracé également les bandes de totalité des éclipses situées trois et six saros avant l'éclipse de -584. Certains historiens avaient émis, à tort, l'hypothèse que la prédiction de Thalès était possible car il aurait eu connaissance de l'éclipse homologue ayant eu lieu trois saros plus tôt. Comme on le constate cette éclipse passe bien plus au nord, suite au décalage en latitudes des éclipses homologues des suites longues d'éclipses.
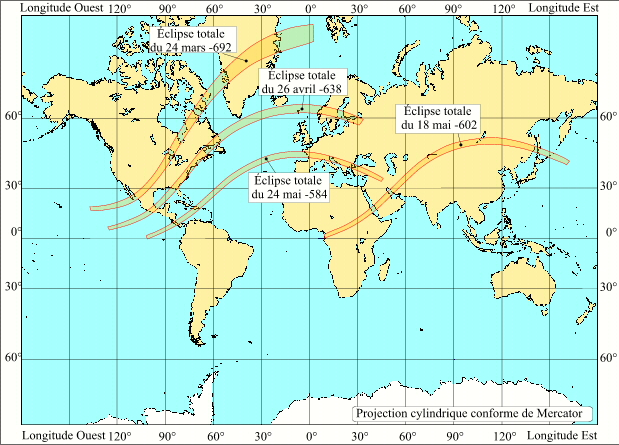
L'éclipse de Thalès et les éclipses homologues
Crédit : IMCCE/Patrick Rocher
Exemple de la détermination du ralentissement de la rotation terrestre
L'éclipse de -135 à Babylone
L'éclipse du Soleil du 15 avril -135 (136 avant J.-C.) est décrite dans deux textes cunéiformes écrits sur des tablettes d'argile se trouvant au British Museum. Outre la mention de l'éclipse, un des textes atteste la visibilité des planètes Mercure, Vénus et Jupiter au moment de l'éclipse. Si l'on ne tient pas compte du ralentissement de la Terre, la bande de centralité passe sur le sud de la France et l'Afrique du Nord. Pour faire passer l'éclipse, donc la bande de centralité sur Babylone, nous avons pris une valeur de la différence Temps terrestre moins Temps universel égale à 3h 14m 23s.
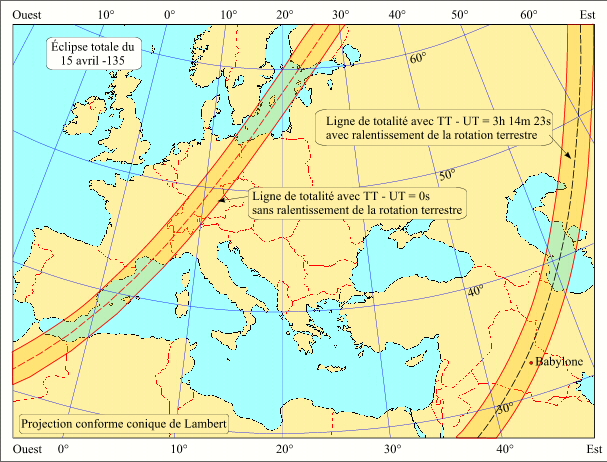
Crédit : IMCCE/Patrick Rocher
La prédiction des éclipses
Une simple observation d'éclipses permet de constater que les éclipses de Lune ont lieu uniquement à la pleine Lune et que les éclipses de Soleil ont lieu uniquement à la nouvelle Lune. La probabilité d'observer une éclipse de Lune en un lieu donné est beaucoup plus forte que la probabilité d'observer une éclipse de Soleil. On pense que les Babyloniens surent très tôt que les éclipses de Lune étaient séparées par cinq ou six lunaisons. Une des plus vieilles prédictions que l'on ait retrouvée date de 731 avant J.-C. et concerne l'éclipse de Lune du 9 avril 731 avant J.-C., le texte précise même que l'éclipse ne sera pas observable car la Lune ne sera pas levée. Des tablettes babyloniennes datant de 475 avant J.-C., contenant des éphémérides de la Lune, donnent dans une colonne un paramètre, qui correspond à la distance entre le centre de la Lune et le centre du cône d'ombre de la Terre, et qui permet de calculer la possibilité des éclipses de Lune. Sur d'autres tablettes figurent également des prédictions d'éclipses de Lune sur une période de 126 ans répartie en périodes de 223 lunaisons correspondant à la période de récurrence des éclipses. Dans chaque saros, 38 éclipses de Lune sont réparties en cinq suites courtes de 8,8,7,8 et 7 éclipses, les éclipses étant espacées entre elles dans les suites par six lunaisons et les suites courtes étant espacées entre elles par cinq lunaisons.
En Chine, on a trouvé les règles du saros chinois pour déterminer les éclipses de Lune dans des textes datant de l'époque de la période des Hans. On ne sait pas si la prédiction des éclipses de Soleil à l'aide du saros date des mêmes époques. La vérification par l'observation de la pertinence du saros pour les éclipses de Soleil étant quasi impossible en raison de la très faible probabilité d'observer une éclipse de Soleil.
Il ne faut surtout pas perdre de vue les faits suivants : le saros permet uniquement de déterminer la date d'une éclipse de Soleil, il ne permet pas de savoir où l'éclipse est observable. La détermination de la visibilité d'une éclipse de Soleil, en un lieu donné, nécessite la connaissance de la parallaxe lunaire et de la position de la Lune au demi-degré près, choses impossibles avant Ptolémée donc avant le milieu du IIe siècle.
Intérêt scientifique des éclipses de Soleil
La liste suivante contient une série de découvertes scientifiques liées aux éclipses de Soleil depuis le XIXe siècle :
- En 1836 : Bailly donne une première description des points brillants qui apparaissent en début et en fin de la totalité.
- En 1842 : Baily donne le nom à la couronne solaire et attribue la couronne au Soleil, et non pas à la Lune.
- En 1851 (28/07) : première photographie d'une éclipse de Soleil (daguerréotype).
- En 1860 (18/07) : première photographie montrant des protubérances solaires, les protubérances appartiennent bien au Soleil, durant cette éclipse on mis également en évidence la polarisation radiale de la lumière coronale.
- En 1868 (18/08) : début de l'analyse spectrale de la couronne et découverte de l'hélium (Janssen, Rayet et Pogson), l'hélium ne sera découvert sur Terre par Ramsay qu'en 1895.
- En 1869 : découverte d'une raie d'émission verte, le nouveau corps est appelé le coronium, ce nouveau corps n'existe pas, en fait, on avait observé le spectre d'éléments lourds fortement ionisés.
- En 1870 : découverte du spectre-éclair par Young, au moment de la totalité le spectre ordinaire du Soleil, avec ses raies sombres, disparaît et est remplacé par une multitude de raies brillantes.
- En 1872 : première observation des plumes, houppe des rayons polaires de la couronne, qui évoquent l'idée des lignes d'un champ magnétique.
- En 1878 : observations de rayons coronaux jusqu'à 6° du Soleil et connexion de la couronne interne (dite couronne K) avec la lumière zodiacale.
Intérêt scientifique des éclipses de Soleil-2
- 1901-1905-1908 : pour expliquer l'avance du périhélie de Mercure, recherche infructueuse durant les éclipses, d'une nouvelle planète proche du Soleil.
- 1919 (19/05) : tentative de vérification de la relativité générale (courbure de l'espace) au voisinage du Soleil, les résultats de cette expérience, tout comme ceux de celle de 1922, ne sont pas probants.
- 1930 : l'invention du coronographe par B. Lyot permet d'observer la couronne solaire et les protubérances en dehors des éclipses totales.
- 1995 : lancement du satellite SoHO (Solar and Heliocentric Observatory) vers le point de Lagrange Terre-Soleil avec plusieurs coronographes équipés de caméra CCD pour l'imagerie permettant l'observation continue du Soleil et de sa couronne.
Malgré la très forte évolution technologique qui permet de nos jours de suivre l'état du Soleil en temps réel, les éclipses totales de Soleil sont encore indispensables à l'étude de la basse couronne. En effet pour des raisons thermiques les coronographes qu'ils soient embarqués dans des sondes spatiales ou qu'ils soient à Terre, ont un diamètre trop important pour permettre la visualisation de la base couronne solaire.
 Introduction
Introduction Prérequis
Prérequis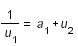
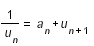

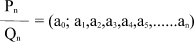
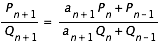
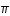
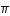 = 3,141592654
= 3,141592654







