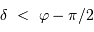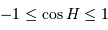 , l'inégalité précédente n'a pas de solution si
, l'inégalité précédente n'a pas de solution si 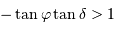 . Le cas limite est donc :
. Le cas limite est donc :
Comme nécessairement 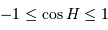 , l'inégalité précédente n'a pas de solution si
, l'inégalité précédente n'a pas de solution si 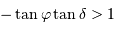 . Le cas limite est donc :
. Le cas limite est donc :
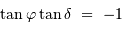
càd
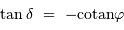
càd 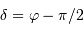 , et en tenant compte de l'inégalité, il n'y a aucune solution si
, et en tenant compte de l'inégalité, il n'y a aucune solution si