Le continuum espace-temps de l'univers
Auteurs: Sylvain Fouquet, François Hammer
- Introduction
- Les principes cosmologiques
- La métrique de l'univers
- Cinématique dans un univers relativiste
- Le décalage spectral vers le rouge
- Exercices
- Les distances cosmologiques
- Exercices
- Equation d'évolution du terme d'accroissement
- Composantes énergétique de l'univers
- Influence de chaque composante
- Exercice
- Evolution sans constante cosmologique
- Exercice
- Evolution avec une constante cosmologique
- Le concept du Big Bang
Introduction
Le précédent chapitre a montré que les galaxies s'éloignent de la Voie Lactée, et ceci d'autant plus vite qu'elles sont éloignées de cette dernière. Pour comprendre ce phénomène physique, il faut envisager l'espace dans le cadre de la relativité générale et non plus dans le cadre de la physique classique de Newton. Depuis Einstein, on sait que l'espace et le temps ne sont pas indépendants. Le continuum espace-temps peut se dilater, se comprimer et cela en fonction de la masse et de l'énergie qu'il contient. Le lien entre le couple masse-énergie et le continuum espace-temps est résumé par l'équation d'Einstein : "masse + énergie équivaut à la courbure de l'espace-temps". Plus l'univers a une forte densité de masse et d'énergie, plus il est courbé et vice-versa. Au-delà d'une densité critique, l'univers est clos et connaîtra une phase de compression après sa phase d'expansion, alors qu'au dessous de cette limite, il se révèle infini et en continuelle expansion. La relativité générale, en plus d'expliquer l'espace-temps de l'univers actuel et futur, permet aussi de le décrire dans le passé. Cette théorie, associée à des hypothèses sur l'univers, prédit que l'univers était plus dense dans le passé et qu'il a même existé un temps où toute la masse était réduite à un point, une singularité, le Big Bang.
Les principes cosmologiques
Distribution de la matière stellaire
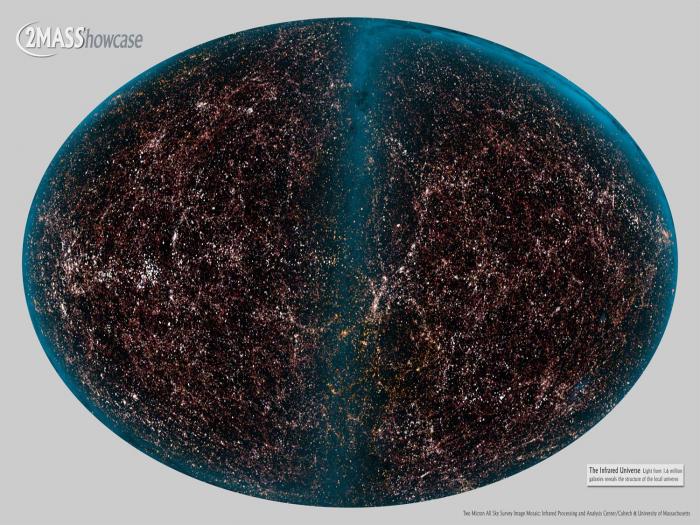
Distribution de sources extra-galactiques émettant dans l'Infrarouge dans l'univers proche. Bien qu'à petite échelle la répartition de matière soit inhomogène, à grande échelle un univers homogène et isotrope se dessine.
Crédit :
The 2MASS Showcase : the Two Micron All Sky Survey (California Institute of Technology)
D'après la relativité générale d'Einstein, pour connaître parfaitement le continuum espace-temps, il faut prendre en compte la distribution du couple masse-énergie de l'univers : la position de chaque atome, leur vitesse ainsi que la position des photons avec leur énergie propre. C'est évidemment impossible en pratique, il faut alors faire les bonnes simplifications pour décrire la distribution d'énergie de l'univers et être ainsi capable de résoudre l'équation d'Einstein et d'accéder au continuum espace-temps de l'Univers. Ces simplifications sont définies sous le terme de "principes cosmologiques" ; ce sont des postulats caractérisant les propriétés de l'univers. En utilisant les données observationnelles de la distribution de la matière dans l'univers de la fin du XXe siècle jusqu'à nos jours, on s'aperçoit que ces principes tendent à être vérifiés dans la partie de l'univers observable.
Principe d'homogénéité et d'isotropie
Les premiers principes de cosmologie concernent le caractère spatial de l'univers. Il est supposé isotrope et homogène. Cela signifie que l'univers n'a pas de direction privilégiée, il est le même quelque soit la direction dans laquelle on le regarde. De plus, il n'a pas de position privilégiée, il est le même quelque soit l'endroit où l'on se trouve.
Principe d'équivalence temporelle
Le second principe cosmologique concerne le temps. Peu importe où l'on se situe dans l'univers, son évolution a été la même. Ce principe est très important lorsque l'on observe des galaxies lointaines. En effet, étant très éloignées, elles sont vues dans le passé. Ces galaxies ne sont donc pas directement les ancêtres de notre Voie Lactée et des autres galaxies proches de nous. Cependant grâce au principe d'équivalence temporelle, ces galaxies sont statistiquement les ancêtres des galaxies de l'univers proche.
Discussion sur les principes cosmologiques
Historiquement, le principe d'homogénéité était généralisé au temps. En effet pour Einstein, l'univers était identique quelque soit le lieu mais aussi l'époque. Cela a généré un univers statique ; ce qui est faux. L'expansion de l'univers montre que l'univers n'est pas statique, l'univers évolue. Toute la suite de ce cours présentera son évolution.
En ce qui concerne les postulats sur le caractère spatial de l'univers, si ce dernier était réellement homogène et isotrope, ce serait un nuage de gaz dont la masse volumique moyenne serait de 1 atome d'hydrogène par mètre cube. Il est évident qu'à petite échelle ces deux propriétés sont fausses ; galaxies, étoiles et planètes le prouvent. Cependant à grande échelle, plusieurs centaines de Mpc, elles paraissent cohérentes avec les données observationnelles. Cela signifie que nous ne décrirons l'évolution de l'univers qu'à grande échelle ; tout comme l'on décrit la terre comme une sphère alors qu'elle est couverte de montagnes la rendant non sphérique à petite échelle. Il est certain que lorsque nous aurons une bonne connaissance du continuum espace-temps à grande échelle, l'étape suivante sera de comprendre et de quantifier l'effet des inhomogénéités de masse tels que les amas ou les grands vides sur le continuum espace-temps.
La métrique de l'univers
Courbure de l'univers



Représentation des trois types de courbure de l'univers : plat, elliptique et hyperbolique.
Crédit :
A. Füzfa (image de fond : Hubble Ultra-Deep Field, télescope spatial Hubble, NASA/ESA).
Le concept de métrique
Avant Einstein, l'espace de la physique classique était considéré comme statique et plat. Deux masses seules supposées sans interaction et sans vitesse relative, séparées dans l'espace, ne pouvaient ni s'éloigner ni se rapprocher. L'espace de la physique classique était aussi décorrélé du temps et comprenait trois dimensions. On pouvait lui joindre un repère cartésien pour donner à chaque point des coordonnées (x, y, z). Dans cet espace, la distance, 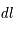 , entre deux points très proches s'écrivait de la manière suivante en coordonnées cartésiennes (x, y, z) et sphériques (
, entre deux points très proches s'écrivait de la manière suivante en coordonnées cartésiennes (x, y, z) et sphériques (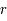 ,
, 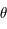 ,
, 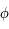 ) :
) :
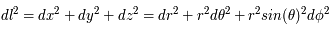
où 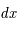 ,
, 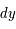 et
et 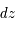 sont les différences de coordonnées en coordonnées cartésiennes et
sont les différences de coordonnées en coordonnées cartésiennes et 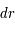 ,
, 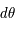 et
et 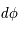 les différences de coordonnées en coordonnées sphériques entre les deux points. Ces deux relations sont ce que l'on appelle la métrique de l'univers dans les coordonnées cartésiennes ou sphériques car elles permettent de mesurer la distance entre deux points proches. Le temps quant à lui est séparé de l'espace et ne fait pas partie de la métrique ; il est absolu, peu importe votre référentiel pour décrire un événement, le temps de ce dernier sera toujours le même.
les différences de coordonnées en coordonnées sphériques entre les deux points. Ces deux relations sont ce que l'on appelle la métrique de l'univers dans les coordonnées cartésiennes ou sphériques car elles permettent de mesurer la distance entre deux points proches. Le temps quant à lui est séparé de l'espace et ne fait pas partie de la métrique ; il est absolu, peu importe votre référentiel pour décrire un événement, le temps de ce dernier sera toujours le même.
La relativité restreinte apporte un premier changement en mêlant espace et temps et définit pour cela une métrique en quatre dimensions notée 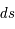 . Entre deux événements E1(x1, y1, z1, t1) et E2(x2, y2, z2, t2) dans un espace à quatre dimensions, la distance est notée :
. Entre deux événements E1(x1, y1, z1, t1) et E2(x2, y2, z2, t2) dans un espace à quatre dimensions, la distance est notée :
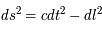 , le même
, le même 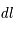 qu'en physique Newtonienne, avec
qu'en physique Newtonienne, avec 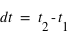 et
et 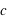 étant la vitesse de la lumière.
étant la vitesse de la lumière.
Ce changement de définition de distance mêlant espace et temps, et surtout l'invariance de cette distance par changement de référentiel, provoque un grand changement conceptuel. L'espace et le temps sont maintenant liés et le temps perd son caractère absolu. Cette métrique de la relativité restreinte est appelée métrique de Minkowski, du nom du mathématicien Hermann Minkowski.
La métrique de notre univers
Avec la relativité générale, Einstein bouleverse encore les concepts d'espace-temps. Après avoir lié l'espace et le temps, Einstein le courbe. En effet, l'espace-temps euclidien est plat, i.e. il correspond à la géométrie euclidienne. Dans ce cas deux droites parallèles ne se croisent jamais, la somme des angles d'un triangle fait 180°, etc. Einstein comprend que la métrique de l'espace-temps n'est pas définie de manière absolue mais qu'elle dépend de la quantité de matière et de la distribution d'énergie dans l'univers. Plusieurs scientifiques, Friedmann, Lemaître, Robertson et Walker, ont aidé à la mise en place de la forme de la métrique de l'univers. En effet, le caractère isotrope et homogène de l'univers contraint la forme de sa métrique. Ainsi, la métrique déduite est appelée métrique FLWR et elle s'écrit sous la forme :
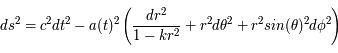
En comparant cette nouvelle métrique avec la métrique de la relativité restreinte, trois caractéristiques apparaissent. Premièrement, la partie temporelle ne change pas, cela implique que l'univers évolue de manière identique dans tout l'espace, c'est le principe d'équivalence temporelle. Deuxièmement, la constante 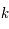 peut pendre trois valeurs possibles, -1, 0 ou 1. En fonction de ces valeurs l'univers sera :
peut pendre trois valeurs possibles, -1, 0 ou 1. En fonction de ces valeurs l'univers sera :
-
hyberbolique et infini (-1), décrit par la géométrie de Lobatchevski ;
-
plat et infini (0), décrit par la géométrie euclidienne ;
-
elliptique et refermé sur lui même donc fini (1), décrit par la géométrie de Riemann.
Troisièmement, cette nouvelle métrique a un terme d'accroissement 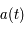 . S'il augmente avec le temps, les distances sont dilatées, sinon elles sont compressées. Ce terme, s'il est constant avec le temps, traduit l'expansion de l'univers. La constante
. S'il augmente avec le temps, les distances sont dilatées, sinon elles sont compressées. Ce terme, s'il est constant avec le temps, traduit l'expansion de l'univers. La constante 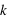 et la fonction
et la fonction 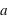 doivent être déterminées par l'observation pour caractériser l'espace-temps de l'univers.
doivent être déterminées par l'observation pour caractériser l'espace-temps de l'univers.
Cinématique dans un univers relativiste
Vitesse
La métrique de l'univers décrite précédemment conduit à des phénomènes inhabituels. Si deux masses sont supposées immobiles l'une par rapport à l'autre, leur distance relative peut tout de même changer. Elle augmente si l'univers est en expansion, elle diminue s'il se comprime. On peut ainsi définir une vitesse d'expansion. Cette vitesse n'en est pas réellement une car elle ne décrit pas le déplacement d'un objet dans l'espace au cours du temps mais le changement de l'espace lui même au cours du temps. La "vitesse d'expansion" entre deux points, distants d'une longueur 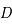 , qui résulte de la métrique de l'univers, est donnée par la relation suivante :
, qui résulte de la métrique de l'univers, est donnée par la relation suivante :
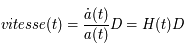 qui est la forme générale de la Loi de Hubble (qui a été présentée au chapitre sur l'expansion de l'univers) pour un univers quelconque. Cette relation montre que la constante de Hubble n'en est pas réellement une. Actuellement, la constante de Hubble vaut près de 70 km.s-1.Mpc-1.
qui est la forme générale de la Loi de Hubble (qui a été présentée au chapitre sur l'expansion de l'univers) pour un univers quelconque. Cette relation montre que la constante de Hubble n'en est pas réellement une. Actuellement, la constante de Hubble vaut près de 70 km.s-1.Mpc-1.
Le décalage spectral vers le rouge
La mesure la plus utile en cosmologie est le décalage spectral vers le rouge (redshift en anglais). Cette mesure est directement reliée à l'expansion de l'univers. Elle est basée sur le ratio entre la valeur de la fonction d'accroissement, 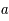 , actuelle,
, actuelle, 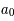 , et dans le passé,
, et dans le passé, 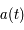 :
:
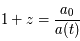
Comme l'univers est en expansion 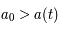 alors
alors 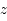 est strictement supérieur à 0. Le décalage spectral vers le rouge tient son nom de la manière de le mesurer. En effet, lorsque l'on reçoit la lumière d'une galaxie lointaine, la longueur d'onde de cette dernière, du fait de l'expansion de l'univers, entre le moment où elle a été émise et le moment où elle est observée par un télescope, s'est dilatée. La lumière apparaît alors plus rouge ; quantitativement
est strictement supérieur à 0. Le décalage spectral vers le rouge tient son nom de la manière de le mesurer. En effet, lorsque l'on reçoit la lumière d'une galaxie lointaine, la longueur d'onde de cette dernière, du fait de l'expansion de l'univers, entre le moment où elle a été émise et le moment où elle est observée par un télescope, s'est dilatée. La lumière apparaît alors plus rouge ; quantitativement 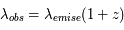 . La mesure de ce décalage vers le rouge permet de connaître l'état de l'expansion de l'univers quand la lumière a été émise.
. La mesure de ce décalage vers le rouge permet de connaître l'état de l'expansion de l'univers quand la lumière a été émise.
Exercices
Auteur: Sylvain Fouquet
 Cinématique dans un univers relativiste
Cinématique dans un univers relativiste
Question 1)
Posons que 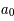 vaut 1 à 13,7 milliards d'années. Si au temps t = 5 milliards d'années
vaut 1 à 13,7 milliards d'années. Si au temps t = 5 milliards d'années 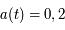 , quel est le décalage spectral d'une galaxie de cette époque ?
, quel est le décalage spectral d'une galaxie de cette époque ?
Question 2)
Si l'univers n'a connu qu'une phase d'expansion, comment classer chronologiquement les galaxies observées ?
Question 3)
Supposons que la constante de Hubble 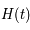 soit constante à tous temps et vaille 70 km.s-1.Mpc-1. Décrire qualitativement le mouvement dû à l'expansion de l'univers d'une galaxie par rapport à la Voie Lactée.
soit constante à tous temps et vaille 70 km.s-1.Mpc-1. Décrire qualitativement le mouvement dû à l'expansion de l'univers d'une galaxie par rapport à la Voie Lactée.
Les distances cosmologiques
Que peut bien signifier le terme de distance dans un univers où l'espace se dilate et donc change continuellement les distances entres les objets ? L'astrophysicien a dû définir différentes distances qui toutes ont un intérêt. Dans un univers classique, les trois distances présentées, distance propre, distance lumineuse et distance angulaire auraient la même valeur. Leur changement de valeur est dû à l'expansion de l'univers et elles se déduisent de la valeur du décalage spectral vers le rouge.
Distance angulaire
De même que pour le flux lumineux, la taille angulaire dépend de la distance. Plus un objet est lointain et plus sa taille angulaire diminue.
Il existe une relation linéaire entre la distance d'un objet, 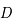 , sa taille réelle,
, sa taille réelle, 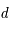 , et sa taille angulaire,
, et sa taille angulaire, 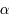 :
:
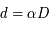
La distance D, qui découle du rapport entre la taille réelle et la taille angulaire, est appelée distance angulaire. Elle n'est plus la même dans un univers relativiste. Un univers plat en expansion tend à faire voir un objet plus grand qu'il ne l'est, un effet de loupe, tandis qu'un univers en contraction réduit la taille angulaire des objets. La distance angulaire devient :
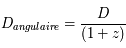
où D est la distance comobile. La distance angulaire est alors identique à la distance propre.
La brillance de surface
Ces nouvelles distances, lumineuses et angulaires, ont des répercussions sur la brillance de surface des galaxies. La brillance d'une galaxie n'est rien d'autre que le rapport entre sa luminosité divisé par sa surface. Cette dernière était constante dans un univers Newtonien mais décroît dans un univers relativiste avec le décalage spectral.
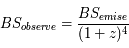
En effet, la surface apparente des galaxies est dilaté par un terme en 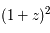 et leur flux est divisé par le terme
et leur flux est divisé par le terme 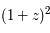 d'où la puissance quatrième.
d'où la puissance quatrième.
Exercices
Auteur: sylvain Fouquet
 Les distance cosmologiques
Les distance cosmologiques
Question 1)
Si aujourd'hui une galaxie se situe à D = 500 Mpc, quelle était sa distance propre à z = 0,6, 1 et 3 ?
Question 2)
Quelle est alors sa distance lumineuse et angulaire pour z = 0,6 ?
Question 3)
Par combien sa brillance de surface est-elle divisée pour les trois décalages spectraux ?
Question 4)
Prenons des galaxies identiques de tailles 10 kpc à différents décalages spectraux. Dans notre univers, pour un décalage spectral de 0,6 une des galaxies a une distance comobile D=2206 Mpc, pour un décalage spectral de 1, une autre galaxie a une distance comobile D=3303 Mpc, pour z = 2, la troisième galaxie a une distance comobile D = 5179 Mpc et pour la dernière galaxie à z = 10, la distance comobile est D = 9440 Mpc. Quelles seront les distances angulaires pour chaque décalage spectral ? Calculez ensuite les tailles angulaires en secondes d'arc et commentez.
Question 5)
Si les galaxies à grands décalages spectraux peuvent être aussi grandes qu'à plus petits décalages spectraux, pourquoi est-il tout de même plus difficile de les voir ?
Question 6)
Soit une galaxie à z = 1 dans un univers en expansion. Via un modèle cosmologique, il est déduit que la lumière de la galaxie fut envoyée il y a huit milliards d'années. Le modèle prédit aussi que la galaxie est aujourd'hui à une distance propre de 3 343 Mpc. Quelle était sa distance propre quand elle a envoyé sa lumière ? Quel distance a traversé la lumière pendant les huit milliards d'années ?
Equation d'évolution du terme d'accroissement
La constante cosmologique
Les équations d'Einstein ont la particularité qu'il est possible de leur ajouter une constante d'intégration, notée 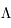 . La valeur de cette constante peut avoir de grandes conséquences dans les propriétés de l'univers. Sa valeur n'a pas de réelle contrainte, si bien qu'elle peut être considérée comme un paramètre libre. Einstein, en son temps, l'avait utilisée pour faire de l'univers un univers statique. Aujourd'hui, cette constante sert à expliquer la possible accélération de l'univers. Dans le cadre de la cosmologie, les équations d'Einstein avec constante cosmologique deviennent :
. La valeur de cette constante peut avoir de grandes conséquences dans les propriétés de l'univers. Sa valeur n'a pas de réelle contrainte, si bien qu'elle peut être considérée comme un paramètre libre. Einstein, en son temps, l'avait utilisée pour faire de l'univers un univers statique. Aujourd'hui, cette constante sert à expliquer la possible accélération de l'univers. Dans le cadre de la cosmologie, les équations d'Einstein avec constante cosmologique deviennent :
(a) 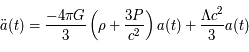
(b) 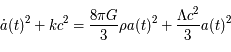
Composantes énergétique de l'univers
Pour résoudre les équations de Friedmann et déterminer 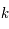 et
et 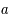 , il faut connaître la valeur de la densité,
, il faut connaître la valeur de la densité, 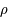 , et de la pression,
, et de la pression, 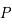 . Pour déterminer ces deux valeurs, il faut prendre en compte l'effet de chaque composante de l'univers dans le bilan masse-énergie.
. Pour déterminer ces deux valeurs, il faut prendre en compte l'effet de chaque composante de l'univers dans le bilan masse-énergie.
La matière non relativiste
La composante la plus simple de l'univers est la matière non relativiste, ayant des vitesses très inférieures à la vitesse de la lumière, avec une pression négligeable par rapport à la densité d'énergie de masse, 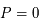 , et une énergie équivalente
, et une énergie équivalente 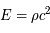 . Les galaxies, les amas de galaxies et le gaz intergalactique forment cette composante énergétique. Cette matière est considérée comme un fluide à l'échelle cosmique (plusieurs centaines de Mpc). Elle est continue et d'une masse volumique constante. Parmi cette composante énergétique, en plus de la matière classique, il semble y avoir une matière dite noire car elle n'interagit que par la gravitation et est donc invisible. La masse volumique de matière actuelle est notée
. Les galaxies, les amas de galaxies et le gaz intergalactique forment cette composante énergétique. Cette matière est considérée comme un fluide à l'échelle cosmique (plusieurs centaines de Mpc). Elle est continue et d'une masse volumique constante. Parmi cette composante énergétique, en plus de la matière classique, il semble y avoir une matière dite noire car elle n'interagit que par la gravitation et est donc invisible. La masse volumique de matière actuelle est notée 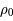 et vaut près de 0,6.10-29 g/cm3. La densité équivalente d'énergie de cette composante de l'univers diminue au cours de l'expansion de l'univers du fait de l'augmentation des volumes :
et vaut près de 0,6.10-29 g/cm3. La densité équivalente d'énergie de cette composante de l'univers diminue au cours de l'expansion de l'univers du fait de l'augmentation des volumes :
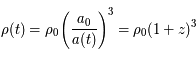
De manière inverse, la densité d'énergie augmente lorsque l'on remonte le temps, pour prendre des valeurs de plus en plus grandes vers l'origine de l'échelle du temps.
Le rayonnement
Sous l'appellation rayonnement, la lumière de même que le gaz relativiste sont pris en compte. Les particules matérielles deviennent relativistes lorsque leurs énergies cinétiques deviennent similaire à leurs énergies de masse, 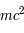 , donc à des vitesses proches de celle de la lumière. En effet, à grande vitesse un gaz relativiste se comporte comme un gaz de photons ayant une pression,
, donc à des vitesses proches de celle de la lumière. En effet, à grande vitesse un gaz relativiste se comporte comme un gaz de photons ayant une pression, 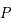 . Cette dernière est reliée par une équation d'état à sa masse volumique,
. Cette dernière est reliée par une équation d'état à sa masse volumique, 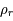 :
:
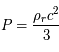
où 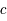 est la vitesse de la lumière. De même que la matière, dans un univers en expansion, la densité d'énergie de ce gaz relativiste se dilue et de plus les photons perdent de l'énergie par la dilatation de leurs longueurs d'onde. De ce fait, la densité d'énergie décroît plus rapidement que celle de la matière. A contrario, cela veut aussi dire qu'elle augmente plus vite lorsque l'on remonte le temps. Ce gaz relativiste décrit alors bien l'état de l'univers durant ses premiers instants lorsqu'il n'était qu'un plasma chaud.
est la vitesse de la lumière. De même que la matière, dans un univers en expansion, la densité d'énergie de ce gaz relativiste se dilue et de plus les photons perdent de l'énergie par la dilatation de leurs longueurs d'onde. De ce fait, la densité d'énergie décroît plus rapidement que celle de la matière. A contrario, cela veut aussi dire qu'elle augmente plus vite lorsque l'on remonte le temps. Ce gaz relativiste décrit alors bien l'état de l'univers durant ses premiers instants lorsqu'il n'était qu'un plasma chaud.
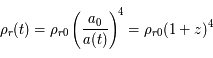
L'énergie noire
Cette dernière forme d'énergie peut être considérée de deux manières. Soit elle est reliée à la constante cosmologique 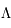 qui serait due à la forme même des équations d'Einstein ; soit elle s'explique par une matière qui aurait des propriétés assez étranges de pression négative qui permettrait d'écrire l'équation d'état suivante :
qui serait due à la forme même des équations d'Einstein ; soit elle s'explique par une matière qui aurait des propriétés assez étranges de pression négative qui permettrait d'écrire l'équation d'état suivante : 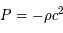 . Dans tous les cas, son influence contribue à l'expansion et peut même l'accélérer.
. Dans tous les cas, son influence contribue à l'expansion et peut même l'accélérer.
Influence de chaque composante
Répartition de l'énergie
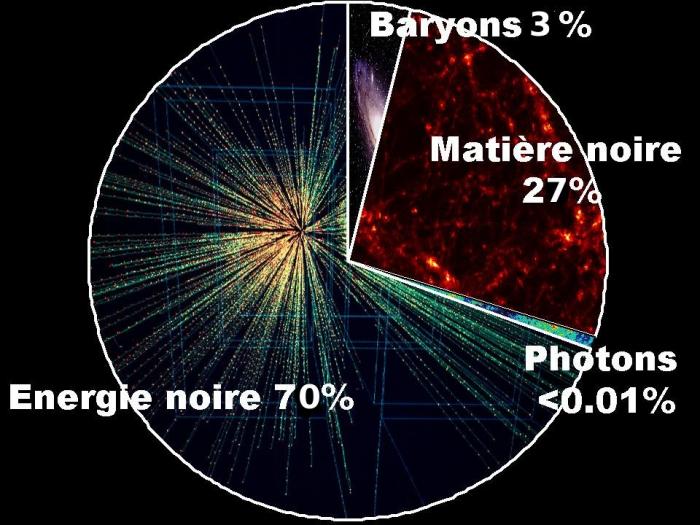
Répartition de l'énergie parmi les différentes composantes de l'univers.
Crédit :
A. Füzfa
Durant l'évolution de l'univers, l'énergie de chaque composante a évolué ; des particules relativistes, en se refroidissant, sont devenues de la matière froide, un plasma de particules s'est transformé en gaz de photons, l'augmentation des volumes a fait décroître les densités énergétiques, etc. Ces changements de la densité énergétique pour chaque composante influe sur la manière qu'a l'espace-temps d'évoluer. Pour mieux comprendre l'influence de chaque composante, elles sont comparées à une densité critique. Les paramètres cosmologiques sont ainsi définis :
- Le premier est celui lié à la matière comprenant la matière classique et la matière noire :
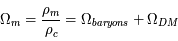 avec
avec 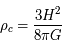 qui vaut
qui vaut 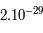 g/cm3 actuellement. Il est estimé pour l'univers actuel à
g/cm3 actuellement. Il est estimé pour l'univers actuel à 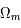 = 0,3 avec
= 0,3 avec 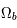 = 0,03 pour les baryons et
= 0,03 pour les baryons et 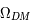 = 0,27 pour la matière noire
= 0,27 pour la matière noire - Le second est le paramètre lié aux rayonnements :
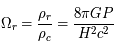 car
car 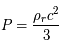 . Il est aujourd'hui négligeable, valant moins de 0,01% du contenu énergétique de l'univers, alors
. Il est aujourd'hui négligeable, valant moins de 0,01% du contenu énergétique de l'univers, alors 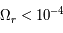
- Le troisième est lié à la constante cosmologique, aussi appelé énergie noire :
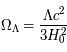 = 0,7. Cette dernière représente donc près de 70 % du contenu masse-énergie de l'univers
= 0,7. Cette dernière représente donc près de 70 % du contenu masse-énergie de l'univers - Le dernier paramètre cosmologique est lié à la courbure de l'espace-temps :
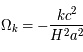
Le choix de ces paramètres se comprend lorsque les équations de Friedmann sont reprises avec ces paramètres cosmologiques. Cela crée deux relations très simples entre ces paramètres et le terme d'accélération :
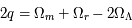
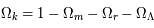
Exercice
Auteur: Sylvain Fouquet
 Transition entre l'époque radiative et stellaire
Transition entre l'époque radiative et stellaire
Actuellement, la densité équivalente d'énergie pour la composante du rayonnement, 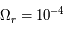 , n'est pas dominante face à la composante de matière,
, n'est pas dominante face à la composante de matière, 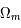 = 0,3. Cependant dans le passé, la composante du rayonnement était plus importante que celle de la matière. Le but de cet exercice est d'avoir une idée grossière de l'époque de transition.
= 0,3. Cependant dans le passé, la composante du rayonnement était plus importante que celle de la matière. Le but de cet exercice est d'avoir une idée grossière de l'époque de transition.
Question 1)
Que valent actuellement les masse volumiques 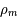 et
et 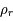 ?
?
Question 2)
Comment évoluent-elles lorsque l'on remonte le temps ?
Question 3)
Pour quel décalage spectral, leur valeur est-elle identique ?
Evolution sans constante cosmologique
Evolution de la fonction d'accroissement
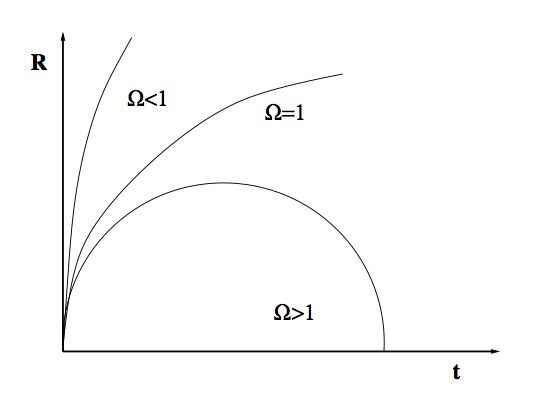
Les trois cas de la fonction d'accroissement pour un univers n'ayant pas de rayonnement ni de constante cosmologique.
Après avoir défini les concepts importants de l'évolution du continuum espace-temps, les sections qui suivent montrent des cas particuliers d'univers en fixant les paramètres cosmologiques et la constante de Hubble. Les premiers exemples d'univers sont uniquement constitués de matière. Le rayonnement est en effet négligeable durant la majeure partie de l'histoire de l'univers ; il ne joue un rôle important que pendant les premiers milliers d'années. De ce fait, l'évolution de l'univers est bien décrit même sans cette composante. La constante cosmologique, 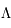 , est supposée être nulle. Le paramètre de la courbure de l'espace se trouve donc être
, est supposée être nulle. Le paramètre de la courbure de l'espace se trouve donc être 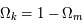 < 1 car
< 1 car 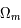 est plus grand que 0. La constante de Hubble est prise valant 70 km.s-1.Mpc-1. Tous les paramètres sont alors connus, il est possible d'en déduire
est plus grand que 0. La constante de Hubble est prise valant 70 km.s-1.Mpc-1. Tous les paramètres sont alors connus, il est possible d'en déduire  et
et 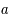 .
.
L'évolution de l'univers prend trois formes différentes en fonction de la valeur de 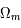 . Si le paramètre de densité est plus grand que 1, donc si la densité de la matière est plus grande que la densité critique, alors
. Si le paramètre de densité est plus grand que 1, donc si la densité de la matière est plus grande que la densité critique, alors 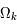 est plus petit que 0 et après une phase d'expansion, l'univers s'effondrera sur lui même. La courbure de l'univers est alors positive et l'univers est fini. Si le paramètre de densité vaut 1,
est plus petit que 0 et après une phase d'expansion, l'univers s'effondrera sur lui même. La courbure de l'univers est alors positive et l'univers est fini. Si le paramètre de densité vaut 1, 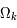 = 0, l'univers est plat et l'expansion continue indéfiniment. Les galaxies s'éloigneront avec des vitesses de plus en plus faibles jusqu'à arriver à une vitesse quasi-nulle dans un temps infini. Le troisième cas offre un univers hyperbolique qui ne fera qu'enfler avec une vitesse d'expansion qui certes diminuera mais ne sera jamais nulle. Le graphique illustre les trois fonctions possibles pour le terme d'accroissement,
= 0, l'univers est plat et l'expansion continue indéfiniment. Les galaxies s'éloigneront avec des vitesses de plus en plus faibles jusqu'à arriver à une vitesse quasi-nulle dans un temps infini. Le troisième cas offre un univers hyperbolique qui ne fera qu'enfler avec une vitesse d'expansion qui certes diminuera mais ne sera jamais nulle. Le graphique illustre les trois fonctions possibles pour le terme d'accroissement, 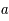 . Seul le cas
. Seul le cas 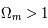 admet pour un temps différent de 0 l'égalité suivante
admet pour un temps différent de 0 l'égalité suivante 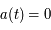 . Cela représente une deuxième singularité appelé le Big Crunch.
. Cela représente une deuxième singularité appelé le Big Crunch.
Exercice
Auteur: Sylvain Fouquet
 L'univers d'Einstein de Sitter
L'univers d'Einstein de Sitter
Cet exercice traite des particularités de l'univers d'Einstein-de Sitter. Bien que faux, cet univers est bien connu pour ses vertus pédagogiques ; en effet tout y est décrit analytiquement. Dans cet univers seule la matière courbe l'espace-temps, le rayonnement et la constante cosmologique sont supposés être nuls. Cet univers est de plus plat.
Question 2)
Dans ce modèle 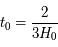 , quel est donc l'âge de l'univers ? Est-ce raisonnable ?
, quel est donc l'âge de l'univers ? Est-ce raisonnable ?
Question 3)
La densité vaut 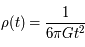 . Que vaudrait-elle à présent et lorsque l'univers avait 380 000 ans ?
. Que vaudrait-elle à présent et lorsque l'univers avait 380 000 ans ?
Question 4)
Pour ce modèle, 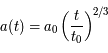 et
et 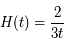 . Est-ce cohérent avec un univers plat ? Comment seront distribuées les galaxies dans une époque très lointaine ?
. Est-ce cohérent avec un univers plat ? Comment seront distribuées les galaxies dans une époque très lointaine ?
Evolution avec une constante cosmologique
Evolution de la fonction d'accroissement
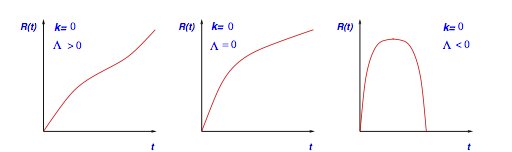
Fonctions du terme d'accroissement dans le cas d'un univers plat. Les trois cas dépendent de la valeur de la constante cosmologique : un univers accéléré (gauche), un univers qui décélère mais toujours en expansion (millieu), un univers qui s'effondre sur lui-même après une phase d'expansion (doite).
La découverte assez récente de la possible accélération de l'expansion de l'univers oblige les astronomes à revoir leurs modèles d'univers composés uniquement de matière. En effet, dans ce dernier cas l'expansion de l'univers ne peut que ralentir. La seule façon d'expliquer une accélération dans le cadre d'un univers homogène et isotrope est l'ajout d'une composante de pression négative : l'énergie du vide ou la constante cosmologique.
La valeur du paramètre de la constante cosmologique avoisine 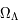 = 0,7. La valeur de la densité de matière actuelle,
= 0,7. La valeur de la densité de matière actuelle, 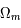 , est 0,3. Ces deux paramètres impliquent un paramètre de courbure égal à 1 - 0,7 - 0,3 = 0, donc un univers plat. De plus, l'apport de la constante cosmologique permet d'avoir un univers dont l'expansion est accélérée. L'univers ne se contente plus de se dilater en décélérant mais il accélère sa dilatation.
, est 0,3. Ces deux paramètres impliquent un paramètre de courbure égal à 1 - 0,7 - 0,3 = 0, donc un univers plat. De plus, l'apport de la constante cosmologique permet d'avoir un univers dont l'expansion est accélérée. L'univers ne se contente plus de se dilater en décélérant mais il accélère sa dilatation.
Ce modèle de l'univers où 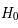 = 70 km.s-1.Mpc-1,
= 70 km.s-1.Mpc-1, 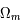 =0,3 et
=0,3 et 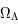 = 0,7 est nommé le modèle
= 0,7 est nommé le modèle 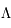 CDM, pour rappeler que la majorité de l'énergie actuellement est sous la forme de la constante
CDM, pour rappeler que la majorité de l'énergie actuellement est sous la forme de la constante 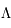 , près de 70%, et qu'une grande partie du reste est contenu dans la matière noire froide (cold dark matter en anglais, d'où le CDM), c'est à dire non relativiste, avec 27% de l'énergie totale. Les 3% restant sont l'univers visible que nous connaissons. Pour l'instant, ce modèle est le modèle standard dans la communauté scientifique, cependant il est frustrant de se rendre compte que 97% du couple énergie-masse de l'univers soit inconnu. Aucun modèle n'explique à ce jour d'où peut provenir l'énergie noire et aucune détection directe n'a permis de mettre en évidence la matière noire. Tout reste encore à faire dans ce domaine.
, près de 70%, et qu'une grande partie du reste est contenu dans la matière noire froide (cold dark matter en anglais, d'où le CDM), c'est à dire non relativiste, avec 27% de l'énergie totale. Les 3% restant sont l'univers visible que nous connaissons. Pour l'instant, ce modèle est le modèle standard dans la communauté scientifique, cependant il est frustrant de se rendre compte que 97% du couple énergie-masse de l'univers soit inconnu. Aucun modèle n'explique à ce jour d'où peut provenir l'énergie noire et aucune détection directe n'a permis de mettre en évidence la matière noire. Tout reste encore à faire dans ce domaine.
Le concept du Big Bang
A la suite de ces deux premiers chapitres de cours, deux aspects essentiels de l'univers sont à noter. L'univers est constitué d'un espace-temps qui n'est pas statique, et ce dernier est en expansion donc l'univers évolue. Si l'espace de l'univers se dilate cela signifie que l'univers était plus dense dans le passé. Les modèles cosmologiques nous apprennent qu'il doit exister un instant dans le passé où la fonction d'accroissement, 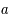 , vaut zéro et où l'univers serait donc sans espace ni temps réduit à un point. Après cette époque l'univers aurait connu une phase d'expansion. Cette idée a pris le nom de Big Bang comme une explosion qui éjecterait tout autour d'elle de la matière. Cependant, cette comparaison fausse la bonne compréhension du Big Bang. En vérité, la matière n'est pas éjectée à partir d'un endroit de l'univers mais c'est l'espace de l'univers lui-même réduit en un point qui se serait dilaté. De plus, cet instant où tout ne serait réduit qu'à un point est une vision purement mathématique. Physiquement nous ne savons pas comment se comporte la matière et donc l'univers quand il atteint de très fortes densités. La singularité du Big Bang signifie un univers sans espace, avec une densité infinie. Les physiciens se méfient des valeurs infinies, elles montrent surtout la méconnaissance du physicien face à un phénomène et le besoin de nouveaux outils mathématiques pour décrire le phénomène physique.
, vaut zéro et où l'univers serait donc sans espace ni temps réduit à un point. Après cette époque l'univers aurait connu une phase d'expansion. Cette idée a pris le nom de Big Bang comme une explosion qui éjecterait tout autour d'elle de la matière. Cependant, cette comparaison fausse la bonne compréhension du Big Bang. En vérité, la matière n'est pas éjectée à partir d'un endroit de l'univers mais c'est l'espace de l'univers lui-même réduit en un point qui se serait dilaté. De plus, cet instant où tout ne serait réduit qu'à un point est une vision purement mathématique. Physiquement nous ne savons pas comment se comporte la matière et donc l'univers quand il atteint de très fortes densités. La singularité du Big Bang signifie un univers sans espace, avec une densité infinie. Les physiciens se méfient des valeurs infinies, elles montrent surtout la méconnaissance du physicien face à un phénomène et le besoin de nouveaux outils mathématiques pour décrire le phénomène physique.
Dans la suite de ce cours, les différentes étapes de l'univers seront exposées. L'époque de recombinaison puis celle de la nucléosynthèse primordiale seront mises en valeur. Ces deux époques sont importantes car leurs conséquences sont visibles actuellement via le Fond Diffus Cosmologique et la répartition de la quantité des atomes dans l'univers. Enfin, l'histoire de l'univers sera détaillée étape par étape, des premiers âges très denses, très chauds et très homogènes jusqu'à notre univers actuel, froid et très inhomogène.




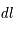 , entre deux points très proches s'écrivait de la manière suivante en coordonnées cartésiennes (x, y, z) et sphériques (
, entre deux points très proches s'écrivait de la manière suivante en coordonnées cartésiennes (x, y, z) et sphériques (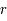 ,
, 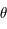 ,
, 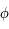 ) :
) :
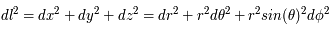
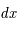 ,
, 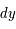 et
et 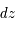 sont les différences de coordonnées en coordonnées cartésiennes et
sont les différences de coordonnées en coordonnées cartésiennes et 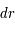 ,
, 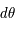 et
et 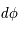 les différences de coordonnées en coordonnées sphériques entre les deux points. Ces deux relations sont ce que l'on appelle la métrique de l'univers dans les coordonnées cartésiennes ou sphériques car elles permettent de mesurer la distance entre deux points proches. Le temps quant à lui est séparé de l'espace et ne fait pas partie de la métrique ; il est absolu, peu importe votre référentiel pour décrire un événement, le temps de ce dernier sera toujours le même.
les différences de coordonnées en coordonnées sphériques entre les deux points. Ces deux relations sont ce que l'on appelle la métrique de l'univers dans les coordonnées cartésiennes ou sphériques car elles permettent de mesurer la distance entre deux points proches. Le temps quant à lui est séparé de l'espace et ne fait pas partie de la métrique ; il est absolu, peu importe votre référentiel pour décrire un événement, le temps de ce dernier sera toujours le même.
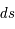 . Entre deux événements E1(x1, y1, z1, t1) et E2(x2, y2, z2, t2) dans un espace à quatre dimensions, la distance est notée :
. Entre deux événements E1(x1, y1, z1, t1) et E2(x2, y2, z2, t2) dans un espace à quatre dimensions, la distance est notée :
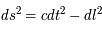 , le même
, le même 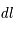 qu'en physique Newtonienne, avec
qu'en physique Newtonienne, avec 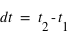 et
et 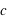 étant la vitesse de la lumière.
étant la vitesse de la lumière.
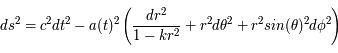
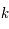 peut pendre trois valeurs possibles, -1, 0 ou 1. En fonction de ces valeurs l'univers sera :
peut pendre trois valeurs possibles, -1, 0 ou 1. En fonction de ces valeurs l'univers sera :
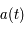 . S'il augmente avec le temps, les distances sont dilatées, sinon elles sont compressées. Ce terme, s'il est constant avec le temps, traduit l'expansion de l'univers. La constante
. S'il augmente avec le temps, les distances sont dilatées, sinon elles sont compressées. Ce terme, s'il est constant avec le temps, traduit l'expansion de l'univers. La constante 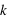 et la fonction
et la fonction 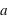 doivent être déterminées par l'observation pour caractériser l'espace-temps de l'univers.
doivent être déterminées par l'observation pour caractériser l'espace-temps de l'univers.
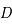 , qui résulte de la métrique de l'univers, est donnée par la relation suivante :
, qui résulte de la métrique de l'univers, est donnée par la relation suivante :
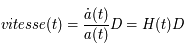 qui est la forme générale de la Loi de Hubble (qui a été présentée au chapitre sur
qui est la forme générale de la Loi de Hubble (qui a été présentée au chapitre sur 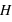 avec le temps. Le terme d'accélération de l'expansion décrit ce changement de vitesse :
avec le temps. Le terme d'accélération de l'expansion décrit ce changement de vitesse :
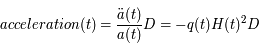 où
où 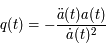
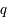 (défini historiquement de la sorte) n'est pas directement l'accélération mais son signe indique s'il y a une accélération (négatif) ou une décélération (positif) car il est multiplié à un terme toujours positif
(défini historiquement de la sorte) n'est pas directement l'accélération mais son signe indique s'il y a une accélération (négatif) ou une décélération (positif) car il est multiplié à un terme toujours positif 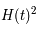 . Actuellement, ce terme semble être négatif et valoir -0,55 m/s2. Son signe négatif implique que l'univers est en expansion accélérée.
. Actuellement, ce terme semble être négatif et valoir -0,55 m/s2. Son signe négatif implique que l'univers est en expansion accélérée.
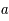 , actuelle,
, actuelle, 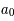 , et dans le passé,
, et dans le passé, 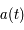 :
:
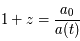
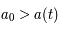 alors
alors 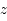 est strictement supérieur à 0. Le décalage spectral vers le rouge tient son nom de la manière de le mesurer. En effet, lorsque l'on reçoit la lumière d'une galaxie lointaine, la longueur d'onde de cette dernière, du fait de l'expansion de l'univers, entre le moment où elle a été émise et le moment où elle est observée par un télescope, s'est dilatée. La lumière apparaît alors plus rouge ; quantitativement
est strictement supérieur à 0. Le décalage spectral vers le rouge tient son nom de la manière de le mesurer. En effet, lorsque l'on reçoit la lumière d'une galaxie lointaine, la longueur d'onde de cette dernière, du fait de l'expansion de l'univers, entre le moment où elle a été émise et le moment où elle est observée par un télescope, s'est dilatée. La lumière apparaît alors plus rouge ; quantitativement 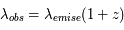 . La mesure de ce décalage vers le rouge permet de connaître l'état de l'expansion de l'univers quand la lumière a été émise.
. La mesure de ce décalage vers le rouge permet de connaître l'état de l'expansion de l'univers quand la lumière a été émise.
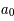 vaut 1 à 13,7 milliards d'années. Si au temps t = 5 milliards d'années
vaut 1 à 13,7 milliards d'années. Si au temps t = 5 milliards d'années 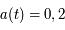 , quel est le décalage spectral d'une galaxie de cette époque ?
, quel est le décalage spectral d'une galaxie de cette époque ?
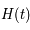 soit constante à tous temps et vaille 70 km.s-1.Mpc-1. Décrire qualitativement le mouvement dû à l'expansion de l'univers d'une galaxie par rapport à la Voie Lactée.
soit constante à tous temps et vaille 70 km.s-1.Mpc-1. Décrire qualitativement le mouvement dû à l'expansion de l'univers d'une galaxie par rapport à la Voie Lactée.
 et à mesurer la distance entre deux points, deux galaxies en pratique. C'est la définition de la distance propre. Cette distance propre dépend du temps par le biais de l'expansion de l'univers. Le lien entre deux distances propres est :
et à mesurer la distance entre deux points, deux galaxies en pratique. C'est la définition de la distance propre. Cette distance propre dépend du temps par le biais de l'expansion de l'univers. Le lien entre deux distances propres est :
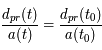 alors
alors 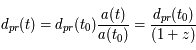
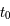 est par définition notre temps présent. On définit la distance comobile par la distance propre au temps actuel,
est par définition notre temps présent. On définit la distance comobile par la distance propre au temps actuel, 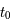 . On fixe la valeur de
. On fixe la valeur de 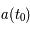 à 1. Dans le passé, les distances propres étaient donc plus petites car z > 0 dans un univers en expansion constante tel que le nôtre.
à 1. Dans le passé, les distances propres étaient donc plus petites car z > 0 dans un univers en expansion constante tel que le nôtre.
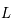 , un observateur à une distance
, un observateur à une distance 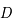 percevra un flux dépendant de cette distance. Plus il est éloigné et plus faible sera le flux de lumière. La décroissance est inversement proportionnelle à la distance au carré :
percevra un flux dépendant de cette distance. Plus il est éloigné et plus faible sera le flux de lumière. La décroissance est inversement proportionnelle à la distance au carré :
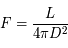
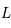 , est connue, il est alors possible d'en déduire la distance de l'objet émetteur par la mesure de son flux. Cette dernière s'appelle la distance lumineuse. Dans un univers relativiste plat, l'expansion ou la contraction de l'univers dilue ou renforce ce flux. De fait, le flux reçu est alors :
, est connue, il est alors possible d'en déduire la distance de l'objet émetteur par la mesure de son flux. Cette dernière s'appelle la distance lumineuse. Dans un univers relativiste plat, l'expansion ou la contraction de l'univers dilue ou renforce ce flux. De fait, le flux reçu est alors :
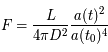 de là
de là 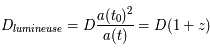
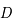 est la distance comobile avec
est la distance comobile avec 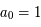 . L'expansion de l'univers (z > 0) fait que les galaxies paraissent plus lointaines.
. L'expansion de l'univers (z > 0) fait que les galaxies paraissent plus lointaines.
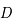 , sa taille réelle,
, sa taille réelle, 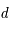 , et sa taille angulaire,
, et sa taille angulaire, 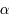 :
:
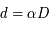
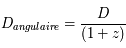
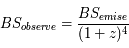
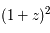 et leur flux est divisé par le terme
et leur flux est divisé par le terme 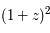 d'où la puissance quatrième.
d'où la puissance quatrième.
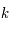 et la fonction d'accroissement
et la fonction d'accroissement 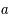 qui définissent la métrique de l'univers. Ces deux quantités sont déduites des équations d'Einstein dans le cadre d'un univers isotrope et homogène. De plus, l'univers étant supposé être un fluide de masse volumique constante, l'énergie équivalente à sa densité de masse est donnée par
qui définissent la métrique de l'univers. Ces deux quantités sont déduites des équations d'Einstein dans le cadre d'un univers isotrope et homogène. De plus, l'univers étant supposé être un fluide de masse volumique constante, l'énergie équivalente à sa densité de masse est donnée par 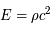 avec en plus une pression
avec en plus une pression 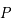 . Les équations d'Einstein dans le cadre de la cosmologie furent obtenues dans les années 1920 par le mathématicien russe Alexandre Friedmann :
. Les équations d'Einstein dans le cadre de la cosmologie furent obtenues dans les années 1920 par le mathématicien russe Alexandre Friedmann :
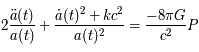
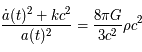
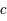 est la vitesse de la lumière et
est la vitesse de la lumière et 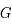 la constante de la gravitation. Ces équations qui dépassent le cadre de ce cours sont seulement là pour illustrer le fait que seules les valeurs de
la constante de la gravitation. Ces équations qui dépassent le cadre de ce cours sont seulement là pour illustrer le fait que seules les valeurs de 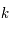 et de
et de 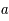 sont inconnues dans ces équations. Des théorèmes mathématiques prouvent que ce système de deux équations à deux inconnues admet des solutions.
sont inconnues dans ces équations. Des théorèmes mathématiques prouvent que ce système de deux équations à deux inconnues admet des solutions.
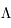 . La valeur de cette constante peut avoir de grandes conséquences dans les propriétés de l'univers. Sa valeur n'a pas de réelle contrainte, si bien qu'elle peut être considérée comme un paramètre libre. Einstein, en son temps, l'avait utilisée pour faire de l'univers un univers statique. Aujourd'hui, cette constante sert à expliquer la possible accélération de l'univers. Dans le cadre de la cosmologie, les équations d'Einstein avec constante cosmologique deviennent :
. La valeur de cette constante peut avoir de grandes conséquences dans les propriétés de l'univers. Sa valeur n'a pas de réelle contrainte, si bien qu'elle peut être considérée comme un paramètre libre. Einstein, en son temps, l'avait utilisée pour faire de l'univers un univers statique. Aujourd'hui, cette constante sert à expliquer la possible accélération de l'univers. Dans le cadre de la cosmologie, les équations d'Einstein avec constante cosmologique deviennent :
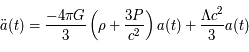
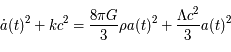
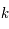 et
et 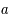 , il faut connaître la valeur de la densité,
, il faut connaître la valeur de la densité, 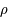 , et de la pression,
, et de la pression, 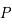 . Pour déterminer ces deux valeurs, il faut prendre en compte l'effet de chaque composante de l'univers dans le bilan masse-énergie.
. Pour déterminer ces deux valeurs, il faut prendre en compte l'effet de chaque composante de l'univers dans le bilan masse-énergie.
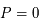 , et une énergie équivalente
, et une énergie équivalente 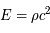 . Les galaxies, les amas de galaxies et le gaz intergalactique forment cette composante énergétique. Cette matière est considérée comme un fluide à l'échelle cosmique (plusieurs centaines de Mpc). Elle est continue et d'une masse volumique constante. Parmi cette composante énergétique, en plus de la matière classique, il semble y avoir une matière dite noire car elle n'interagit que par la gravitation et est donc invisible. La masse volumique de matière actuelle est notée
. Les galaxies, les amas de galaxies et le gaz intergalactique forment cette composante énergétique. Cette matière est considérée comme un fluide à l'échelle cosmique (plusieurs centaines de Mpc). Elle est continue et d'une masse volumique constante. Parmi cette composante énergétique, en plus de la matière classique, il semble y avoir une matière dite noire car elle n'interagit que par la gravitation et est donc invisible. La masse volumique de matière actuelle est notée 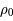 et vaut près de 0,6.10-29 g/cm3. La densité équivalente d'énergie de cette composante de l'univers diminue au cours de l'expansion de l'univers du fait de l'augmentation des volumes :
et vaut près de 0,6.10-29 g/cm3. La densité équivalente d'énergie de cette composante de l'univers diminue au cours de l'expansion de l'univers du fait de l'augmentation des volumes :
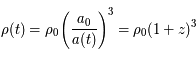
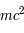 , donc à des vitesses proches de celle de la lumière. En effet, à grande vitesse un gaz relativiste se comporte comme un gaz de photons ayant une pression,
, donc à des vitesses proches de celle de la lumière. En effet, à grande vitesse un gaz relativiste se comporte comme un gaz de photons ayant une pression, 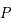 . Cette dernière est reliée par une équation d'état à sa masse volumique,
. Cette dernière est reliée par une équation d'état à sa masse volumique, 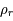 :
:
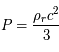
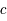 est la vitesse de la lumière. De même que la matière, dans un univers en expansion, la densité d'énergie de ce gaz relativiste se dilue et de plus les photons perdent de l'énergie par la dilatation de leurs longueurs d'onde. De ce fait, la densité d'énergie décroît plus rapidement que celle de la matière. A contrario, cela veut aussi dire qu'elle augmente plus vite lorsque l'on remonte le temps. Ce gaz relativiste décrit alors bien l'état de l'univers durant ses premiers instants lorsqu'il n'était qu'un plasma chaud.
est la vitesse de la lumière. De même que la matière, dans un univers en expansion, la densité d'énergie de ce gaz relativiste se dilue et de plus les photons perdent de l'énergie par la dilatation de leurs longueurs d'onde. De ce fait, la densité d'énergie décroît plus rapidement que celle de la matière. A contrario, cela veut aussi dire qu'elle augmente plus vite lorsque l'on remonte le temps. Ce gaz relativiste décrit alors bien l'état de l'univers durant ses premiers instants lorsqu'il n'était qu'un plasma chaud.
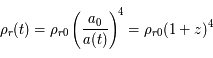
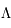 qui serait due à la forme même des équations d'Einstein ; soit elle s'explique par une matière qui aurait des propriétés assez étranges de pression négative qui permettrait d'écrire l'équation d'état suivante :
qui serait due à la forme même des équations d'Einstein ; soit elle s'explique par une matière qui aurait des propriétés assez étranges de pression négative qui permettrait d'écrire l'équation d'état suivante : 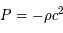 . Dans tous les cas, son influence contribue à l'expansion et peut même l'accélérer.
. Dans tous les cas, son influence contribue à l'expansion et peut même l'accélérer.

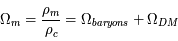 avec
avec 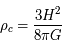 qui vaut
qui vaut 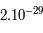 g/cm3 actuellement. Il est estimé pour l'univers actuel à
g/cm3 actuellement. Il est estimé pour l'univers actuel à 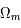 = 0,3 avec
= 0,3 avec 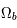 = 0,03 pour les baryons et
= 0,03 pour les baryons et 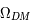 = 0,27 pour la matière noire
= 0,27 pour la matière noire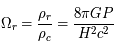 car
car 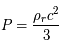 . Il est aujourd'hui négligeable, valant moins de 0,01% du contenu énergétique de l'univers, alors
. Il est aujourd'hui négligeable, valant moins de 0,01% du contenu énergétique de l'univers, alors 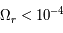
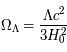 = 0,7. Cette dernière représente donc près de 70 % du contenu masse-énergie de l'univers
= 0,7. Cette dernière représente donc près de 70 % du contenu masse-énergie de l'univers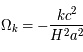
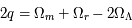
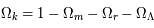
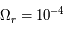 , n'est pas dominante face à la composante de matière,
, n'est pas dominante face à la composante de matière, 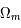 = 0,3. Cependant dans le passé, la composante du rayonnement était plus importante que celle de la matière. Le but de cet exercice est d'avoir une idée grossière de l'époque de transition.
= 0,3. Cependant dans le passé, la composante du rayonnement était plus importante que celle de la matière. Le but de cet exercice est d'avoir une idée grossière de l'époque de transition.
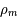 et
et 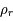 ?
?

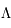 , est supposée être nulle. Le paramètre de la courbure de l'espace se trouve donc être
, est supposée être nulle. Le paramètre de la courbure de l'espace se trouve donc être 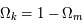 < 1 car
< 1 car 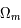 est plus grand que 0. La constante de Hubble est prise valant 70 km.s-1.Mpc-1. Tous les paramètres sont alors connus, il est possible d'en déduire
est plus grand que 0. La constante de Hubble est prise valant 70 km.s-1.Mpc-1. Tous les paramètres sont alors connus, il est possible d'en déduire  et
et 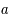 .
.
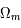 . Si le paramètre de densité est plus grand que 1, donc si la densité de la matière est plus grande que la densité critique, alors
. Si le paramètre de densité est plus grand que 1, donc si la densité de la matière est plus grande que la densité critique, alors 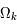 est plus petit que 0 et après une phase d'expansion, l'univers s'effondrera sur lui même. La courbure de l'univers est alors positive et l'univers est fini. Si le paramètre de densité vaut 1,
est plus petit que 0 et après une phase d'expansion, l'univers s'effondrera sur lui même. La courbure de l'univers est alors positive et l'univers est fini. Si le paramètre de densité vaut 1, 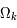 = 0, l'univers est plat et l'expansion continue indéfiniment. Les galaxies s'éloigneront avec des vitesses de plus en plus faibles jusqu'à arriver à une vitesse quasi-nulle dans un temps infini. Le troisième cas offre un univers hyperbolique qui ne fera qu'enfler avec une vitesse d'expansion qui certes diminuera mais ne sera jamais nulle. Le graphique illustre les trois fonctions possibles pour le terme d'accroissement,
= 0, l'univers est plat et l'expansion continue indéfiniment. Les galaxies s'éloigneront avec des vitesses de plus en plus faibles jusqu'à arriver à une vitesse quasi-nulle dans un temps infini. Le troisième cas offre un univers hyperbolique qui ne fera qu'enfler avec une vitesse d'expansion qui certes diminuera mais ne sera jamais nulle. Le graphique illustre les trois fonctions possibles pour le terme d'accroissement, 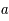 . Seul le cas
. Seul le cas 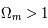 admet pour un temps différent de 0 l'égalité suivante
admet pour un temps différent de 0 l'égalité suivante 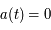 . Cela représente une deuxième singularité appelé le Big Crunch.
. Cela représente une deuxième singularité appelé le Big Crunch.
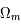 ,
, 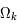 ,
, 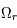 et
et 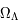 ?
?
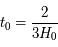 , quel est donc l'âge de l'univers ? Est-ce raisonnable ?
, quel est donc l'âge de l'univers ? Est-ce raisonnable ?
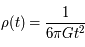 . Que vaudrait-elle à présent et lorsque l'univers avait 380 000 ans ?
. Que vaudrait-elle à présent et lorsque l'univers avait 380 000 ans ?
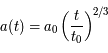 et
et 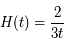 . Est-ce cohérent avec un univers plat ? Comment seront distribuées les galaxies dans une époque très lointaine ?
. Est-ce cohérent avec un univers plat ? Comment seront distribuées les galaxies dans une époque très lointaine ?

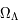 = 0,7. La valeur de la densité de matière actuelle,
= 0,7. La valeur de la densité de matière actuelle, 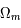 , est 0,3. Ces deux paramètres impliquent un paramètre de courbure égal à 1 - 0,7 - 0,3 = 0, donc un univers plat. De plus, l'apport de la constante cosmologique permet d'avoir un univers dont l'expansion est accélérée. L'univers ne se contente plus de se dilater en décélérant mais il accélère sa dilatation.
, est 0,3. Ces deux paramètres impliquent un paramètre de courbure égal à 1 - 0,7 - 0,3 = 0, donc un univers plat. De plus, l'apport de la constante cosmologique permet d'avoir un univers dont l'expansion est accélérée. L'univers ne se contente plus de se dilater en décélérant mais il accélère sa dilatation.
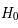 = 70 km.s-1.Mpc-1,
= 70 km.s-1.Mpc-1, 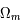 =0,3 et
=0,3 et 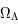 = 0,7 est nommé le modèle
= 0,7 est nommé le modèle 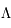 CDM, pour rappeler que la majorité de l'énergie actuellement est sous la forme de la constante
CDM, pour rappeler que la majorité de l'énergie actuellement est sous la forme de la constante 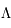 , près de 70%, et qu'une grande partie du reste est contenu dans la matière noire froide (cold dark matter en anglais, d'où le CDM), c'est à dire non relativiste, avec 27% de l'énergie totale. Les 3% restant sont l'univers visible que nous connaissons. Pour l'instant, ce modèle est le modèle standard dans la communauté scientifique, cependant il est frustrant de se rendre compte que 97% du couple énergie-masse de l'univers soit inconnu. Aucun modèle n'explique à ce jour d'où peut provenir l'énergie noire et aucune détection directe n'a permis de mettre en évidence la matière noire. Tout reste encore à faire dans ce domaine.
, près de 70%, et qu'une grande partie du reste est contenu dans la matière noire froide (cold dark matter en anglais, d'où le CDM), c'est à dire non relativiste, avec 27% de l'énergie totale. Les 3% restant sont l'univers visible que nous connaissons. Pour l'instant, ce modèle est le modèle standard dans la communauté scientifique, cependant il est frustrant de se rendre compte que 97% du couple énergie-masse de l'univers soit inconnu. Aucun modèle n'explique à ce jour d'où peut provenir l'énergie noire et aucune détection directe n'a permis de mettre en évidence la matière noire. Tout reste encore à faire dans ce domaine.
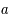 , vaut zéro et où l'univers serait donc sans espace ni temps réduit à un point. Après cette époque l'univers aurait connu une phase d'expansion. Cette idée a pris le nom de Big Bang comme une explosion qui éjecterait tout autour d'elle de la matière. Cependant, cette comparaison fausse la bonne compréhension du Big Bang. En vérité, la matière n'est pas éjectée à partir d'un endroit de l'univers mais c'est l'espace de l'univers lui-même réduit en un point qui se serait dilaté. De plus, cet instant où tout ne serait réduit qu'à un point est une vision purement mathématique. Physiquement nous ne savons pas comment se comporte la matière et donc l'univers quand il atteint de très fortes densités. La singularité du Big Bang signifie un univers sans espace, avec une densité infinie. Les physiciens se méfient des valeurs infinies, elles montrent surtout la méconnaissance du physicien face à un phénomène et le besoin de nouveaux outils mathématiques pour décrire le phénomène physique.
, vaut zéro et où l'univers serait donc sans espace ni temps réduit à un point. Après cette époque l'univers aurait connu une phase d'expansion. Cette idée a pris le nom de Big Bang comme une explosion qui éjecterait tout autour d'elle de la matière. Cependant, cette comparaison fausse la bonne compréhension du Big Bang. En vérité, la matière n'est pas éjectée à partir d'un endroit de l'univers mais c'est l'espace de l'univers lui-même réduit en un point qui se serait dilaté. De plus, cet instant où tout ne serait réduit qu'à un point est une vision purement mathématique. Physiquement nous ne savons pas comment se comporte la matière et donc l'univers quand il atteint de très fortes densités. La singularité du Big Bang signifie un univers sans espace, avec une densité infinie. Les physiciens se méfient des valeurs infinies, elles montrent surtout la méconnaissance du physicien face à un phénomène et le besoin de nouveaux outils mathématiques pour décrire le phénomène physique.