![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation23.png)
La solution
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} + \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \cos( \alpha _{\mathrm{A}} - \alpha _{\mathrm{B}}) \right]](../pages_reperes/equations_referentiel/equation23.png)
s'écrit dans ce cas, avec 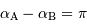 .
.
![d = {\mathrm{acos}} \left[ \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} - \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} \right] = \pi - {\mathrm{acos}} \left[ \cos \delta _{\mathrm{A}} \cos \delta _{\mathrm{B}} - \sin \delta _{\mathrm{A}} \sin \delta _{\mathrm{B}} \right]](../pages_reperes/equations_referentiel/equation25.png)
Et donc, dans ce cas :
![d = \pi - {\mathrm{acos}} [ \cos ( \delta _{\mathrm{A}} + \delta _{\mathrm{B}}) ] = \pi - | \delta _{\mathrm{A}} + \delta _{\mathrm{B}}|](../pages_reperes/equations_referentiel/equation26.png)
Si, de plus, les déclinaisons sont égales, on trouve alors
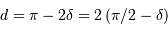
La distance angulaire, en passant par les pôles, est bien égale à 2 fois la colatitude ; la colatitude est le complément à 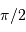 (ou 90 deg) de la latitude.
(ou 90 deg) de la latitude.