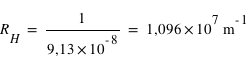Présentation du modèle de Bohr
Dans le modèle de Bohr semi-classique, l'électron tourne autour du noyau dans une orbite circulaire, comme une planète autour du Soleil. Un électron en orbite autour du noyau devrait rayonner et, perdant son énergie par rayonnement, tomber sur le noyau. Or ceci ne se produit pas, puisque les atomes sont stables. Bohr supposa alors qu'il existe certaines orbites où l'électron n'émet pas de rayonnement. Ceci arrive chaque fois que le moment de la quantité de mouvement de l'électron est un multiple entier de h/2π (où h est la constante de Planck 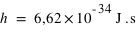 ): on numérote par 1, 2, ...., n les orbites successives ainsi permises.
): on numérote par 1, 2, ...., n les orbites successives ainsi permises.
Application à l'atome d'hydrogène
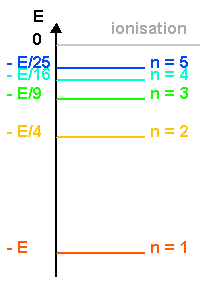
Considérons l'atome d'hydrogène. Son électron ne peut se trouver que sur l'une de ces orbites. Chaque orbite correspond à un niveau d'énergie donné de l'atome: le niveau d'énergie le plus bas, dit niveau fondamental, correspond à l'orbite la plus proche du noyau, qui porte le numéro n=1. Plus n est grand et plus l'orbite a un grand rayon, ce qui veut dire que l'énergie de l'atome est plus élevée. La valeur de n infinie correspond à une orbite de rayon infini, c'est-à-dire à l'ionisation de l'atome. L'énergie correspondante est de 13,6eV.
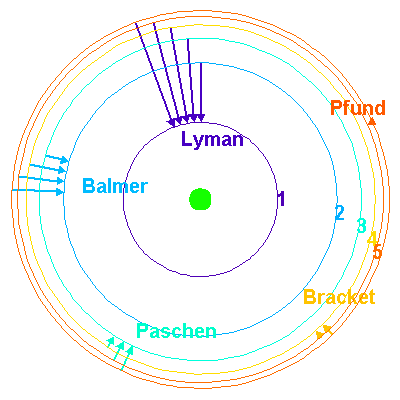
L'atome d'hydrogène ne peut absorbe ou émettre qu'un photon d'énergie bien définie.
Lorsque l'électron retombe d'un niveau excité dans un niveau de plus basse énergie, il y a émission d'un rayonnement qui transporte exactement l'énergie correspondant à la différence d'énergie entre les deux niveaux.
Pour qu'il y ait émission il faut que l'énergie du niveau initial soit supérieur à l'énergie du niveau final c'est-à-dire que En > Em, n étant le niveau initial et m le niveau final. Or la mécanique quantique montre que pour l'atome d'hydrogène, l'énergie des différents niveaux est définie par l'expression :
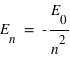
où n est un entier (il s'agit des différents niveaux), et E0 l'énergie nécessaire pour ioniser l'atome d'hydrogène à partir de son niveau fondamental, (valeur est égale à 13,6 eV).
Le photon ainsi émis a une énergie égale à la différence d'énergie entre les deux orbites soit Em-En. Cette énergie correspond, par l'équation de Planck (E=hν), à une onde électromagnétique de fréquence ν bien définie. Le saut d'énergie se manifeste donc par une raie d'émission dans le spectre de l'atome. On en déduit alors :
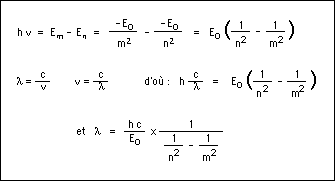
ou encore
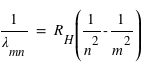
avec la constante de Rydberg :
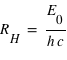
L'atome d'hydrogène peut aussi absorber de l'énergie, ceci lui permettant de passer d'un niveau inférieur à un niveau supérieur, par exemple en absorbant un photon. Mais ceci n'est possible que si le photon possède exactement l'énergie nécessaire, c'est-à-dire la différence d'énergie entre le niveau d'arrivée et le niveau de départ.
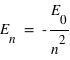
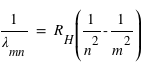
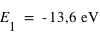 .
.
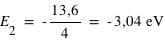
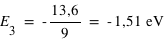
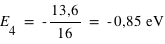
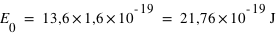 .
On en déduit alors la valeur :
.
On en déduit alors la valeur :