Le TP se déroulera suivant le plan suivant :
- expliquer la notion d’échelle appliquée au ciel. Sur une carte de géographie, un centimètre = des kilomètres ; ici, un centimètre = des secondes de degré, c’est-à-dire un angle sur le ciel
- on distribuera les documents aux élèves et on examinera le premier document pour bien comprendre ce qu’est une image du ciel ; puis on comparera avec le deuxième document pour bien voir qu’un objet se déplace (un astéroïde) et que c’est sa position à l’instant du cliché que l’on cherche.
- le troisième document montre que certaines étoiles connues vont servir de bornes pour calculer la position de notre astéroïde ; le quatrième document donne les positions des étoiles du troisième document : bien comprendre la correspondance
- on identifiera les objets à mesurer sur le premier document. Chaque élève ou groupe d’élèves choisira bien entendu ses propres étoiles. Il est important que tous ne choisissent pas les mêmes étoiles.
- on effectuera les mesures avec soin en reportant les valeurs sur la feuille dite "cinquième document" et on fera les calculs demandés pour arriver à une valeur finale
- on comparera avec la valeur exacte et on remarquera que la moyenne des valeurs obtenues par tous est proche du bon résultat ; on comparera aussi avec les valeurs des éphémérides.
Ce TP peut avoir comme prolongement le travail par Internet puisque images, catalogues d’étoiles et éphémérides sont disponibles sur Internet.
Leur détection et leur identification
Ayant vu comment l'image se formait derrière un télescope, on va choisir le télescope adéquat pour obtenir des images permettant d'effectuer les mesures.
La mesure de la position des astéroïdes, des satellites des planètes et des comètes est essentielle à plusieurs titres:
- étude dynamique de leur mouvement: les observations permettent de valider les modèles dynamiques théoriques construits;
- prédictions de leurs positions, en particulier dans le cas des astéroïdes s'approchant de la Terre et pouvant présenter un danger;
- étude de la distribution des astéroïdes dans le système solaire afin d'avoir des informations sur l'origine et la stabilité à long terme de ce système.
Nous allons donc étudier des images de ces corps, détecter ceux-ci, les identifier et mesurer leurs positions.
Ces objets ne sont visibles depuis la Terre que comme des petits points lumineux sans diamètre apparent semblables aux étoiles. Seul leur mouvement trahit leur présence et c’est le changement de position en quelques minutes qui va trahir leur présence. Les comètes sont souvent entourées d’un halo lumineux : la chevelure et la queue.

Crédit :
J.E. Arlot/CNRS/OHP

Crédit :
J.E. Arlot/CNRS/OHP
Ci-contre, deux images de l’astéroïde (53) Kalypso prises le 22 septembre 2000 à une demie heure d’intervalle. On détecte l’astéroïde grâce à son déplacement entre les deux poses. Les éphémérides donnent aussi sa position qui permet de le retrouver parmi les étoiles.
Identification d'un corps du système solaire parmi les étoiles et le principe du rattachement à ces étoiles
La technique photographique ou d'imagerie électronique se pratique donc avec un télescope fournissant une image d'une partie du ciel, un "champ" dont la dimension est mesurée en angle sur le ciel.
Bien que l'on connaisse a priori la distance focale du télescope utilisé, celle-ci n'est pas connue avec suffisamment de précision pour transformer des mesures en millimètres sur l'image en angles sur le ciel. Pour cela, il est nécessaire d'avoir une image de l'objet inconnu entouré d'images d'étoiles de catalogue dont on connaît très précisément les coordonnées. Le processus de réduction astrométrique va permettre de calculer l'échelle de l'image qui transformera des millimètres en angle et l'orientation qui indiquera la direction de l'est selon l'équateur céleste. Cela nous conduira aux positions en ascension droite et déclinaison cherchées. Ce processus de réduction astrométrique doit être appliqué pour chaque image pour plusieurs raisons:
- l'image réalisée est plane alors que l'image d'un morceau de sphère céleste au foyer d'un télescope est sphérique. Il faut tenir compte de la projection réalisée;
- l'optique du télescope n'est pas parfaite et engendre des déformations du champ (pas d'isotropie de l'échelle ni de l'orientation) et les caractéristiques du télescope (focale de l'optique) ont la fâcheuse tendance à se modifier avec la température;
- la réfraction atmosphérique rapproche les astres du zénith: une correction spécifique est aussi nécessaire et dépend de l'état de l'atmosphère au dessus du télescope.
Ces effets sont pris en compte en introduisant des inconnues dans le processus de réduction. Un plus grand nombre d'étoiles de rattachement est alors nécessaire pour étalonner le champ observé. La haute précision astrométrique est à ce prix.
Les catalogues d'étoiles ont beaucoup progressé au cours des dernières années et on dispose actuellement d'un "bornage" dense du ciel par les étoiles de catalogue.
On trouvera ci-dessous le processus d'identification d'objet et de choix d'étoiles d'étalonnage dans le cas du satellite Phoebe de Saturne (que l'on observe comme un astéroïde).

Crédit :
J.E. Arlot/CNRS/OHP

Crédit :
Digitized Sky Survey/HST
Ci-contre, en premier, le champ du satellite Phoebé de Saturne, pris le 21 mars 1998 à 2h 52m UTC à l'observatoire de Haute Provence (champ de 12 minutes de degré, télescope de 120cm). On identifie l'astre mobile de deux manières:
- par son déplacement entre deux poses successives;
- l'astre n'est pas présent sur une image de référence de même champ faite avec un télescope de Schmidt à une autre date (image suivante). Cette image est disponible sur Internet sur le site du DSS (Digitized Sky Survey).
L'objet mobile Phoebé est indiqué par la flèche jaune.
Crédit :
Guide Star Catalogue/USNO
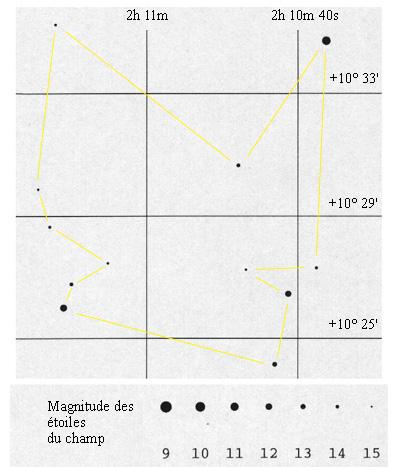
Il reste à identifier des étoiles connues de catalogue qui permettront d'étalonner le champ (détermination de l'échelle en angle par millimètre et de l'orientation par rapport au repère équatorial des ascensions droites et des déclinaisons). Ci-dessus une carte de champ extraite du "Guide Star catalogue", un catalogue très dense d'étoiles construit pour permettre le pointage du Télescope Spatial.
Nous allons appliquer cette méthode au champ de l'astéroïde Kalypso et utiliser le catalogue USNO A2 à la place du Guide Star Catalogue qui contient ne contient pas assez d'étoiles pour ce champ.
Identification de l'astéroïde (53) Kalypso parmi les étoiles

Crédit :
Digitized Sky Survey/HST/Mont Palomar

Crédit :
J.E. Arlot/CNRS/OHP
Ci-dessus à droite le champ de l'astéroïde (53) Kalypso pris le 22 septembre 2000 avec le télescope de 120 cm de l'observatoire de Haute-Provence. le champ fait 12 x 12 minutes de degré. l'astéroïde est brillant (magnitude 12) et aisément identifiable. Sur l’image de gauche prise à une autre date (DSS), l'astéroïde n'est pas présent.
Connaissant la position approchée de l’astéroïde, on peut tracer une carte des étoiles du champ observé à partir d’un catalogue. Il faudra identifier les étoiles du catalogue sur l’image observée pour pouvoir effectuer le rattachement de la position de l’astéroïde aux étoiles connues. Ces étoiles vont nous permettre d’étalonner le champ, d’en déterminer les constantes.
Nous utiliserons le catalogue USNO A2 qui contient 526 millions d’étoiles et donc un grand nombre d’étoiles de notre champ. Le tracé de ces étoiles est fourni ci-après dans le troisième document servant à la réalisation du TP. L'objet brillant au centre, non reconnu comme étoile du catalogue, est l'astéroïde (53) Kalypso
Ce type de carte de champ peut être obtenu sur le serveur du Centre de Données Astronomiques de Strasbourg. On lui fournit les coordonnées du centre du champ et on visualise une image du champ avec les étoiles de catalogue.
Pour effectuer le calcul à la main de la position de l'astéroïde Kalypso, on utilisera les documents papiers accompagnant le TP. Ces documents, présentés ci-après, pourront être photocopiés ou imprimés à partir des fichiers.

Premier document: image du champ de Kalypso sur lequel on identifiera l'astéroïde et les étoiles d'étalonnage et sur lequel on effectuera les mesures avec un double décimètre ou un quadrillage transparent.
Crédit :
J.E. Arlot/CNRS/OHP

Deuxième document: image du même champ SANS l'astéroïde, issu des archives du DSS accessible par Internet. C'est ce document qui permet d’identifier sans peine l'astéroïde sur le premier document.
Crédit :
Digitized Sky Survey/HST/Mont Palomar
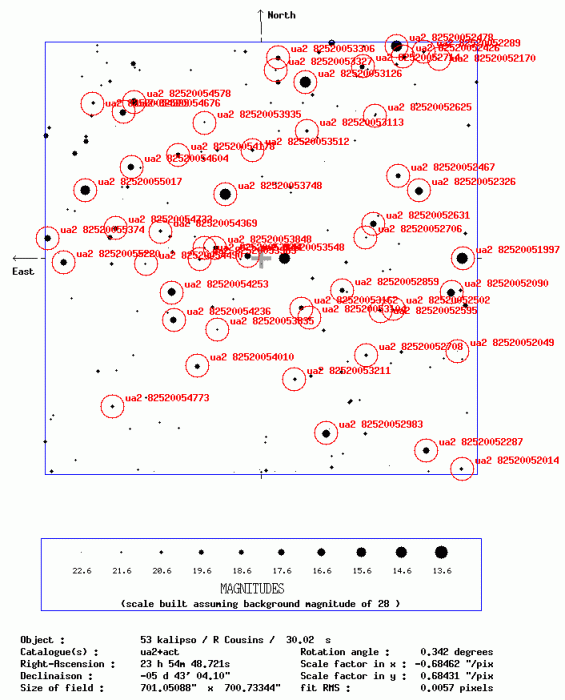
Troisième document: carte du champ où apparaissent les étoiles du catalogue. En comparant avec le premier document on sélectionnera, par exemple, trois étoiles d'étalonnage du champ. On les choisira de façon à être sûr de l'identification (éviter les étoiles trop proches) et bien réparties autour de Kalypso.
Crédit :
CDS/USNO
Quatrième document: la table des positions des étoiles du catalogue destinées au calcul de l'échelle.
Catalogue d'étoiles
positions théoriques des étoiles du catalogue USNO A2 repérées sur l'image
Explications du contenu des colonnes
- ID: numéro d'identification des étoiles que l'on retrouvera sur la carte
- Ascension droite, déclinaison: position théorique de l'étoile
- Magnitude: brillance de l'étoile pour aider à l'identification (plus le nombre est élevé, plus l'étoile est faiblement brillante)
Catalogue d'étoiles
| Identificateur |
Ascension droite |
Déclinaison |
Magnitude |
| 82520053748 |
23 54 52.542 |
-05 41 20.51 |
12.40 |
| 82520053126 |
23 54 43.819 |
-05 38 19.71 |
12.50 |
| 82520052478 |
23 54 33.875 |
-05 37 21.41 |
12.50 |
| 82520051997 |
23 54 26.803 |
-05 43 06.50 |
12.80 |
| 82520055017 |
23 55 07.756 |
-05 41 12.72 |
13.30 |
| 82520052983 |
23 54 41.765 |
-05 47 48.88 |
13.90 |
| 82520054578 |
23 55 02.377 |
-05 38 51.13 |
14.30 |
| 82520052326 |
23 54 31.498 |
-05 41 15.74 |
14.70 |
| 82520054253 |
23 54 58.399 |
-05 43 59.81 |
14.90 |
| 82520052090 |
23 54 28.026 |
-05 44 01.35 |
15.00 |
| 82520052287 |
23 54 30.910 |
-05 48 17.70 |
15.30 |
| 82520055220 |
23 55 10.202 |
-05 43 09.38 |
15.70 |
| 82520053548 |
23 54 50.166 |
-05 43 00.56 |
15.80 |
| 82520052631 |
23 54 36.460 |
-05 42 09.80 |
15.80 |
| 82520055374 |
23 55 11.900 |
-05 42 30.74 |
15.90 |
| 82520052714 |
23 54 37.482 |
-05 37 54.20 |
16.10 |
| 82520054604 |
23 55 02.720 |
-05 40 35.10 |
16.20 |
| 82520054676 |
23 55 03.555 |
-05 39 06.47 |
16.20 |
| 82520054236 |
23 54 58.238 |
-05 44 44.29 |
16.40 |
| 82520053162 |
23 54 44.374 |
-05 44 26.35 |
16.40 |
| 82520052426 |
23 54 33.115 |
-05 37 38.89 |
16.60 |
| 82520053306 |
23 54 46.732 |
-05 37 39.43 |
16.70 |
| 82520054010 |
23 54 55.667 |
-05 45 58.29 |
16.70 |
| 82520052467 |
23 54 33.765 |
-05 40 51.53 |
16.90 |
| 82520052859 |
23 54 39.897 |
-05 43 57.57 |
17.10 |
| 82520053989 |
23 54 55.368 |
-05 43 06.07 |
17.20 |
| 82520053848 |
23 54 53.706 |
-05 42 47.13 |
17.20 |
| 82520054369 |
23 54 59.647 |
-05 42 20.52 |
17.30 |
| 82520054733 |
23 55 04.462 |
-05 42 14.82 |
17.30 |
| 82520052502 |
23 54 34.472 |
-05 44 27.53 |
17.40 |
| 82520053512 |
23 54 49.552 |
-05 40 09.49 |
17.50 |
| 82520054773 |
23 55 04.940 |
-05 47 03.27 |
17.60 |
| 82520054929 |
23 55 06.888 |
-05 38 52.18 |
17.60 |
| 82520052014 |
23 54 27.025 |
-05 48 48.26 |
17.70 |
| 82520054178 |
23 54 57.649 |
-05 40 16.77 |
17.90 |
| 82520052708 |
23 54 37.362 |
-05 45 42.49 |
18.00 |
| 82520052595 |
23 54 35.776 |
-05 44 31.15 |
18.00 |
| 82520053211 |
23 54 45.163 |
-05 46 20.79 |
18.10 |
| 82520053113 |
23 54 43.660 |
-05 39 38.96 |
18.50 |
| 82520052625 |
23 54 36.232 |
-05 39 14.89 |
18.50 |
Cinquième document: la feuille de calcul. Cette feuille donne la succession des étapes de calcul afin d'arriver à la position de l'astéroïde Kalypso par interpolation des mesures effectuées sur le premier document.
Feuille de calcul de position
Cette feuille permet d'effectuer les calculs qui permettront de déterminer les positions alpha(a) et delta(a) de l'astéroïde à partir de ses positions mesurées Xa et Ya et des positions théoriques des étoiles alpha(i), alpha(j), ... et delta(i), delta(j),... grâce aux formules suivantes:
alpha(a) = alpha(i) + {(alpha(i)-alpha(j))/(Xj-Xi)} x (Xa-Xi)
delta(a) = delta(i) + {(delta(i)-delta(j))/(Yj-Yi)} x (Ya-Yi)
Feuille de calcul de position
| Valeurs de i, j
(étoiles choisies) |
calcul en ascension droite |
valeurs numériques |
calcul en déclinaison |
valeurs numériques |
|
alpha(i) sexagésimal |
|
delta(i) sexagésimal |
|
|
alpha(i) décimal |
|
delta(i) décimal |
|
|
alpha(j) sexagésimal |
|
delta(j) sexagésimal |
|
|
alpha(j) décimal |
|
delta(j) décimal |
|
|
alpha(j)-alpha(i) décimal |
|
delta(j)-delta(i) décimal |
|
|
Xi |
|
Yi |
|
|
Xj |
|
Yj |
|
|
Xj-Xi |
|
Yj-Yi |
|
| Position mesuré de l'astéroïde: |
Xa |
|
Ya |
|
|
Xa-Xi |
|
Ya-Yi |
|
| Echelles de l'image: |
échelle en ascension droite: (alpha(j)-alpha(i))/(Xj-Xi) |
|
échelle en déclinaison: (delta(j)-delta(i))/(Yj-Yi) |
|
|
alpha(a) décimal =
alpha(i)+échelle x (Xa-Xi) |
|
delta(a) décimal =
delta(i)+échelle x (Ya-Yi) |
|
| Résultat: |
alpha(a) sexagésimal |
|
delta(a) sexagésimal |
|
On va maintenant voir le résultat du calcul précis effectué en étalonnant le champ comme indiqué dans le cours à l’aide de constantes de cible pour déterminer l’échelle, l’orientation et les déformations du champ..
Notons que si un grand nombre de calcul à la main sont réalisés simultanément avec des étoiles et des mesures différentes, on constatera que la majorité des résultats seront proches du bon résultat.
On comparera également les résultats aux valeurs théoriques calculées avec les modèles dynamiques du mouvement de l'astéroïde Kalypso (grâce aux serveurs sur Internet indiqués sur la page des liens Internet). Ces valeurs théoriques, données dans les pages suivantes avec la valeur observée précise, montrent qu'elles diffèrent selon le modèle utilisé et qu'il est donc utile d'effectuer des observations qui aideront à améliorer les modèles utilisés.
Crédit :
J.E. Arlot/CNRS/OHP
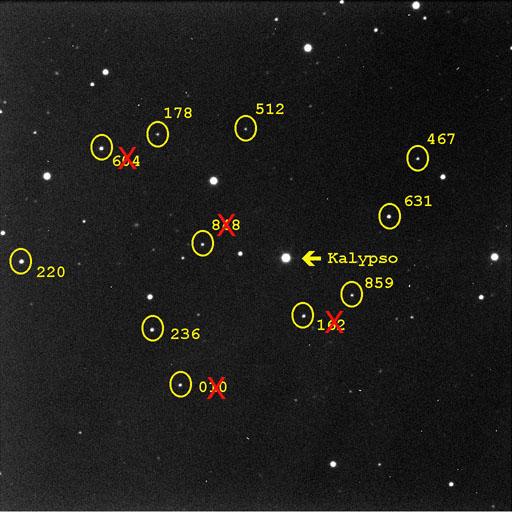
Choix des étoiles devant servir au rattachement et à l'étalonnage du champ
Le catalogue USNO A2 contient beaucoup d'étoiles et toutes ne sont pas susceptibles de servir pour l'étalonnage du champ: il faut choisir des étoiles bien ponctuelles (pour en déterminer la position avec précision), pas trop brillantes (les étoiles brillantes ont un mouvement propre dont nous ne tenons pas compte ici) et bien situées par rapport à Kalypso (on diminue l'erreur sur la mesure en choisissant des étoiles éloignées mais situées de part et d'autre de Kalypso).
Les étoiles dans un cercle jaune sont les étoiles sélectionnées pour l'étalonnage; les étoiles barrées d'une croix rouge sont celles qui se sont avérées mauvaises, comme on le verra dans l'algorithme de calcul présenté à la page suivante.
Le calcul de l'échelle du cliché (passage des positions mesurées en millimètres aux positions angulaires -ascension droite et déclinaison-) se fait à partir des positions des étoiles du catalogue. Deux étoiles suffisent mais l'emploi de plusieurs autres étoiles et la moyenne des mesures vont augmenter la précision.
Une fois les mesures sur l'image réalisées et les étoiles de catalogue choisies, le logiciel va déterminer la transformation qui fera passer des millimètres sur l'image aux positions angulaires sur le ciel. La précision et la qualité du calcul sera estimée grâce aux étoiles en surnombre: comme nous avons plus de données que nécessaires, le logiciel doit résoudre un système comportant plus d'équations que d'inconnues. La méthode des moindres carrés est une méthode statistique qui va minimiser les erreurs commises. Chaque étoile va se positionner par rapport aux autres avec un "résidu" d'autant plus grand que la position théorique ou mesurée de l'étoile est mauvaise, c'est-à-dire incompatible avec celle des autres étoiles.
Premier calcul de positions
#--------------------------------------------------------------------------------
# > Parametres de la réduction :
# + Date : 22/09/2000
# + Heure (UTC) : 22 h 22 m 37,9 s
# + Jour julien : 2451810.432383
#
# + Nombre d'objets réduits : 1
# + Nombre d'étoiles choisies : 11
# + Degré du polynôme : 1
# + Nombre de coefficients de la transformation : 2x4
#
# > Solution astrométrique (position alpha et delta de Kalypso) :
# ascension droite: 23h 54m 46,1440s déclinaison: -05° 43' 4,547"
#
# > Constantes de la transformation:
# + en X : A(1) = 0.00139 +/- 0.27833
# A(2) = -0.00439 +/- 0.00170
# A(3) = 0.68412 +/- 0.00120
constante donnant l'échelle en X (est-ouest) de l'image en secondes de degré par pixel
# A(4) = 0.00000 +/- 0.00001
# + en Y : B(1) = -0.01200 +/- 0.17874
# B(2) = 0.68352 +/- 0.00109
constante donnant l'échelle en Y (nord-sud) de l'image en secondes de degré par pixel
# B(3) = 0.00328 +/- 0.00077
# B(4) = 0.00000 +/- 0.00001
#
# > Résidus pour chaque étoile (en secondes de degré en ascensuin droite et en déclinaison) :
# alpha delta
# 2 1.80590 0.12206 UA2_082520053848
# 2 0.31413 -0.45747 UA2_082520053162
# 2 -0.74127 0.93308 UA2_082520054010
# 2 -0.32438 -0.78833 UA2_082520054236
# 2 0.31699 0.02706 UA2_082520055220
# 2 -1.25452 0.43274 UA2_082520054604
# 2 0.34332 -0.38676 UA2_082520054178
# 2 0.03323 0.40231 UA2_082520053512
# 2 -0.28936 -0.19379 UA2_082520052467
# 2 -0.24685 0.45504 UA2_082520052631
# 2 -0.11133 0.10896 UA2_082520052859
Deuxième calcul
L'étoile UA2_082520053848 ayant un résidu très fort, on va recommencer le calcul en l'éliminant.
#--------------------------------------------------------------------------------
# > Parametres de la réduction : :
# + Date : 22/09/2000
# + Heure (UTC) : 22 h 22 m 37,9 s
# + Jour julien : 2451810.432383
#
# + Nombre d'objets réduits : 1
# + Nombre d'étoiles choisies : 10
# + Degré du polynôme : 1
# + Nombre de coefficients de la transformation: 2x4
#
# > Solution astrométrique (position alpha et delta de Kalypso) :
# 1 ascension droite: 23h 54m 46,1328s déclinaison: -05° 43' 4,552"
#
# > Constantes de la transformation:
# + en X : A(1) = 0.00087 +/- 0.19587
# A(2) = -0.00433 +/- 0.00115
# A(3) = 0.68396 +/- 0.00081
constante donnant l'échelle en X (est-ouest) de l'image en secondes de degré par pixel
# A(4) = 0.00000 +/- 0.00001
# + en Y : B(1) = -0.01304 +/- 0.20234
# B(2) = 0.68353 +/- 0.00118
constante donnant l'échelle en Y (nord-sud) de l'image en secondes de degré par pixel
# B(3) = 0.00327 +/- 0.00083
# B(4) = 0.00000 +/- 0.00001
#
# > Résidus pour chaque étoile (en secondes de degré en ascension droite et en déclinaison) :
# alpha delta
# 2 0.48937 -0.45143 UA2_082520053162
# 2 -0.52822 0.94044 UA2_082520054010
# 2 -0.10951 -0.78090 UA2_082520054236
# 2 0.56728 0.03574 UA2_082520055220
# 2 -1.03071 0.44049 UA2_082520054604
# 2 0.54311 -0.37985 UA2_082520054178
# 2 0.19516 0.40790 UA2_082520053512
# 2 -0.19164 -0.19043 UA2_082520052467
# 2 -0.12136 0.45936 UA2_082520052631
# 2 0.04638 0.11439 UA2_082520052859
#--------------------------------------------------------------------------------
Troisième calcul
On va éliminer les trois étoiles UA2_082520054010 UA2_082520053162 UA2_082520054604, qui ont un résidu trop important.
#--------------------------------------------------------------------------------
# > Paramètres de la réduction :
# + Date : 22/09/2000
# + Heure (UTC) : 22 h 22 m 37,9 s
# + Jour julien : 2451810.432383
#
# + Nombre d'objets réduits : 1
# + Nombre d'étoiles choisies : 7
# + Degré du polynôme : 1
# + Nombre de coefficients de la transformation : 2x4
#
# > Solution astrométrique (position alpha et delta de Kalypso) :
# 1 ascension droite: 23h 54m 46,1381s déclinaison: -05° 43' 4,635"
#
# > Constantes de la transformation :
#
# + en X : A(1) = 0.03729 +/- 0.05869
# A(2) = -0.00371 +/- 0.00040
# A(3) = 0.68499 +/- 0.00022
constante donnant l'échelle en X (est-ouest) de l'image en secondes de degré par pixel
# A(4) = 0.00000 +/- 0.00000
# + en Y : B(1) = 0.00032 +/- 0.21348
# B(2) = 0.68418 +/- 0.00145
constante donnant l'échelle en Y (nord-sud) de l'image en secondes de degré par pixel
# B(3) = 0.00277 +/- 0.00079
# B(4) = 0.00000 +/- 0.00001
#
# > Résidus pour chaque étoile (en secondes de degré en ascension droite et en déclinaison) :
# alpha delta
# 2 -0.17783 -0.36279 UA2_082520054236
# 2 0.13728 0.47162 UA2_082520055220
# 2 -0.03863 -0.40857 UA2_082520054178
# 2 -0.10602 0.38440 UA2_082520053512
# 2 0.04433 -0.20424 UA2_082520052467
# 2 -0.01781 0.42496 UA2_082520052631
# 2 0.05272 0.10933 UA2_082520052859
#--------------------------------------------------------------------------------
Les résidus sont maintenant convenables et on va adopter la position calculée de Kalypso:
alpha = 23h 54m 46,1381s; delta = -05° 43' 4,635"
On pourra comparer les valeurs trouvées à la main avec cette valeur ou avec les valeurs calculées par les serveurs d'éphémérides de l'Institut de mécanique céleste (IMCCE), du Jet Propulsion Laboratory (NASA) ou du MPC (Minor Planet Center).
Valeur de l'IMCCE: alpha = 23h 54m 46,09s; delta = -5° 43' 5,13"
Valeur du MPC: alpha = 23h 54m 46s; delta = -5° 43' 0"
Valeur du JPL: alpha = 23h 54m 45,53s; delta = -5° 43' 9,6"
Tout ce qui a été effectué dans les pages précédentes peut être refait en utilisant Internet. On peut:
- aller chercher des images nouvelles d'astéroïdes ou d'autres objets sur des serveurs aux adresses suivantes :
- aller consulter des catalogues du CDS à l’adresse suivante (utilisation délicate à préparer par l’enseignant) :
- faire fonctionner les serveurs de calcul d'éphémérides des adresses suivantes :








