Champ: Astronomie Soleil Terre Lune
Niveau: **
Temps: 4h00
 Prérequis
Prérequis
TP en relation avec les cours :
 Objectifs
Objectifs
Le but de ce TP est de comparer la taille du disque lunaire avec la taille de l'ombre de la Terre et d'en déduire le rayon lunaire et la distance Terre-Lune.
 Introduction
Introduction
Les calculs développés dans ce TP supposent que la Lune est à une distance fixe de la Terre, et la Terre à une distance fixe du Soleil.
La figure 1 montre le schéma d'une éclipse de Soleil et d'une éclipse de Lune. Par le plus pur hasard, les diamètres apparents de la Lune et du Soleil vus depuis la surface de la Terre sont presque égaux (nous les supposerons strictement les mêmes dans la suite).
En supposant que le rayon de la Terre est très petit devant celui du Soleil, on voit sur la figure 2 que l'angle du cône d'ombre de la Lune est approximativement égal à l'angle du cône d'ombre de la Terre.
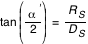
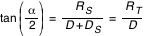 donc
donc 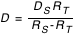
alors 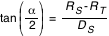 et comme
et comme 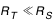
on obtient : 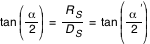
On voit alors sur la figure 3, en reportant le cône d'ombre de la Lune à côté de celui de la Terre, que le diamètre de la Terre est égal à la somme du diamètre de l'ombre de la Terre (à la distance de la Lune) et du diamètre de la Lune.
Si DO est le diamètre de l'ombre de la Terre à la distance de la Lune, DL le diamètre de la Lune et DT le diamètre de la Terre, on a
DT = DL+DO qui donne 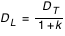 , en posant
, en posant 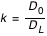 .
Or k est également égal au rapport du diamètre angulaire de l'ombre de la Terre (à la distance de la Lune) par le diamètre angulaire de la Lune, et peut être estimé observationnellement. Connaissant alors le diamètre absolu de la Lune et son diamètre apparent, il est aisé de calculer sa distance.
.
Or k est également égal au rapport du diamètre angulaire de l'ombre de la Terre (à la distance de la Lune) par le diamètre angulaire de la Lune, et peut être estimé observationnellement. Connaissant alors le diamètre absolu de la Lune et son diamètre apparent, il est aisé de calculer sa distance.
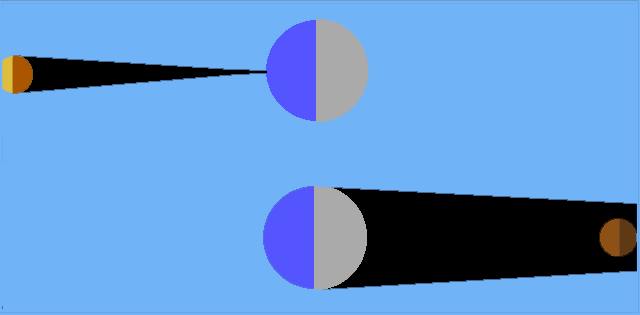
Eclipse de Soleil (en haut) et éclipse de Lune (en bas)
Crédit :
ASM
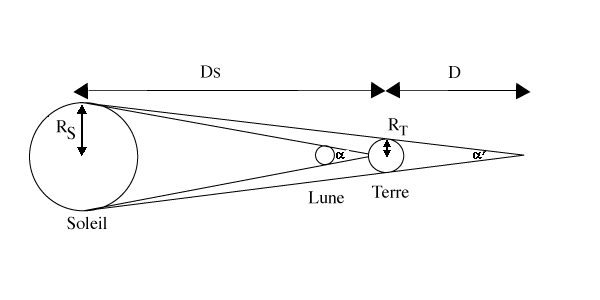
Comparaison des cônes d'ombre de la Lune et de la Terre
Crédit :
ASM
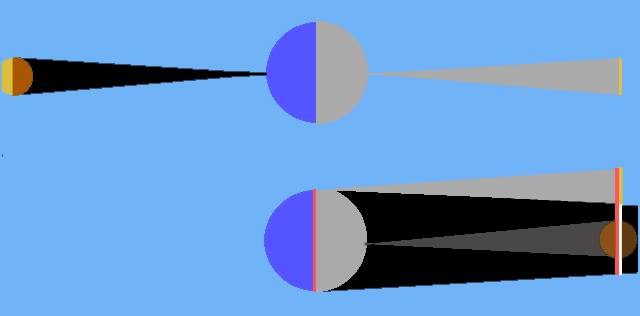
Le diamètre de la Terre DT (en rouge) est la somme du diamètre de la Lune DL (orange) et du diamètre de l'ombre de la Terre au niveau de la Lune D0 (blanc).
Crédit :
ASM
Eclipse du 09 nov 2003



Images de l'éclipse de Lune du 9 novembre 2003
Crédit :
Nicolas Bivert
Eclipse du 09 nov 2003



Images de l'éclipse de Lune (couleurs inversées)
Crédit :
ASM / Nicolas Bivert
Première méthode
Cette méthode utilise une photo d'une éclipse de Lune pour estimer le rapport k précédemment défini. Trois photos de l'éclipse du 9 novembre 2003 sont fournies ci-contre. Sur chaque photo, nous allons mesurer le rayon de l'ombre et celui de la Lune. Pour cela on préfèrera utiliser les photos après avoir inversé les couleurs. Imprimer les images en les mettant dans le coin bas gauche de la page, de telle sorte que le centre du cercle (ombre de la Terre) soit sur la feuille de papier.
Commencer par tracer des points sur le bord de la Lune et sur le bord de l'ombre. Choisir ensuite des couples de points sur l'un ou l'autre des bords et tracer la médiatrice à la règle et au compas. Ceci donnera une zone possible pour le centre de la Lune et pour le centre de l'ombre, le centre d'un cercle devant être sur la médiatrice de n'importe quel segment composé de deux point du cercle. Choisir un centre pour la Lune et un pour l'ombre et mesurer le rayon de la Lune et celui de l'ombre. Estimer l'erreur sur chacune de ces mesures. Donner une estimation de k puis du rapport entre le rayon de la Lune et celui de la Terre.
Le rapport k peut être déduit des éphémérides en calculant le rapport du rayon de l'Ombre (U. Radius) par le demi diamètre de la Lune (S.D.).
Comparer avec les résultats observationnels et commenter.
Deuxième méthode
Lors d'une éclipse de Lune, on peut définir différents moments correspondant aux contacts du bord lunaire avec l'ombre de la Terre comme le montre la figure ci-contre.
Les contacts
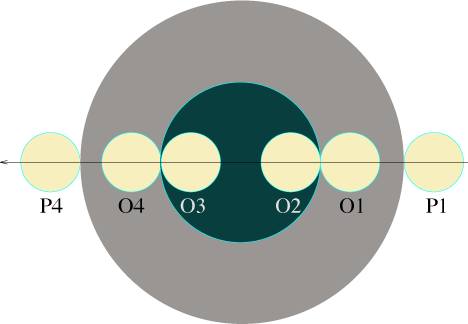
P1 : premier contact extérieur avec la pénombre, O1 : premier contact extérieur avec l'ombre, O2 : premier contact intérieur avec l'ombre, O3 : dernier contact intérieur avec l'ombre, O4 : dernier contact extérieur avec l'ombre et P4 : dernier contact extérieur avec la pénombre.
Crédit :
ASM
Si l'on arrive à mesurer les instants de ces contacts, il est alors possible de calculer k. En effet, le temps mis par la Lune pour parcourir son diamètre angulaire est égal à O2-O1 ou O4-O3. De même, le temps mis par la Lune pour parcourir l'ombre de la Terre est O3-O1 ou O4-O2. Le rapport k est donc égal, par exemple, à 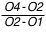 .
.
Ces calculs ne sont exacts que si le centre de la Lune passe par le centre de l'ombre de la Terre. C'est rarement le cas comme le montre les éphémérides des éclipses des 21 janvier 2000 et 9 janvier 2001. On voit sur les graphiques de ces éclipses que O2-O1 ou O4-O3 est plus grand que le temps mis par la Lune pour parcourir son diamètre et que O3-O1 ou O4-O2 est au contraire plus petit que le temps mis pour parcourir l'ombre de la Terre sur un de ses diamètre. Le calcul précédent donne donc une valeur majorante de la taille de la Lune.
Quelles valeurs trouve-t-on pour ces deux éclipses ?
Première méthode
Une fois la taille absolue de la Lune connue, sa distance peut être calculée aisément pour peu que l'on connaisse son diamètre angulaire.
Une méthode assez simple à mettre en oeuvre consiste à masquer la Lune avec une bille de diamètre connu et à l'éloigner jusqu'à ce qu'elle coïncide avec la Lune. Le rapport entre le diamètre de la bille et sa distance par rapport à l'oeil de l'observateur est égal à celui du diamètre de la Lune et de la distance Terre-Lune (d'après le théorème de Thalès).
Un montage simple peut être imaginé pour réaliser cette expérience qui peut être faite sur la pleine Lune avant ou après l'éclipse.
Deuxième méthode
Le diamètre angulaire de la Lune peut également être calculé par chronométrage. Sachant que la Lune met 29,5305882 jours pour se retrouver à la même phase (mois synodique ou lunaison), c'est-à-dire pour faire 360 degrés par rapport au Soleil, le diamètre angulaire de la Lune (en degrés) est égal à :
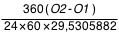 avec O2-O1 mesuré en minutes.
avec O2-O1 mesuré en minutes.
La distance Terre-Lune est alors égale au diamètre absolu de la Lune divisé par la tangente de son diamètre angulaire. Faire le calcul avec les données fournies par les éphémérides. Comparer avec les distances réelles données par la parallaxe de la Lune (valeur H.P. dans les tables) dans les éphémérides.
Conclusion ?
La distance moyenne Terre-Lune peut également être déduite par la gravitation. Connaissant le rayon de la Terre par la méthode d'Érathostène (RT ≈ 6 400 km) et la valeur de l'accélération de la pesanteur à la surface de la Terre (g = 9,78 m.s-2 à l'équateur), on peut en déduire la valeur de la constante GM par la formule 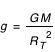 .
.
En supposant que la masse de la Lune est négligeable devant celle de la Terre (elle est de 1/81 masse terrestre), la troisième loi de Kepler nous donne : 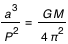 où a est la distance Terre-Lune et P est la période de rotation anomalistique de la Lune autour de la Terre (P=27,55 jours correspondant au temps écoulé entre deux passages au périgée).
où a est la distance Terre-Lune et P est la période de rotation anomalistique de la Lune autour de la Terre (P=27,55 jours correspondant au temps écoulé entre deux passages au périgée).
Calculer la masse de la Terre et la distance Terre-Lune par cette méthode.
 Conclusion
Conclusion
C'est Aristarque de Samos (310-230 avant J.-C.) qui utilisa le premier les éclipses de Lune pour calculer la distance de la Lune et sa taille, relatives à la taille de la Terre. Hipparque (190-120 avant J.-C.) puis Ptolémée (120-180 après J.-C.) améliorèrent cette méthode de sorte que les astronomes anciens avait une bonne idée de ces grandeurs. Aristarque et de nombreux astronomes jusqu'au 17 ème siècle, mesurèrent également la distance du Soleil en mesurant l'angle que faisait la Lune avec le Soleil lors du premier ou du dernier quartier. Mais cette méthode, bien que rigoureusement exacte du point de vue géométrique, était en réalité inapplicable et donnait une distance 20 fois trop petite de sorte que, jusqu'au 17ème siècle, la distance de la Lune fut la seule distance astronomique connue avec une certaine précision. L'avènement des lunettes et télescopes permis ensuite de mesurer précisément des angles plus petits et de déterminer la parallaxe diurne des planètes proches et d'en déduire la distance du Soleil. De nos jours, la distance de la Lune est mesurée avec des radars ou des lasers dont la lumière est réfléchie par des petits miroirs posés sur le sol lunaire par les missions Apollo.
Les méthodes présentées ici permettent de déterminer la distance de la Lune à quelques dizaines de pourcents près, en supposant que la Lune et la Terre ont des orbites circulaires. En réalité, les excentricité de l'orbite de la Terre (e=0,017) et de celle de la Lune (e=0,05) font varier la taille de l'ombre de la Terre et le diamètre apparent de la Lune respectivement. De plus, l'excentricité de l'orbite de la Lune est telle que la distance Terre-Lune varie de 7 pourcents (de 356 400 à 406 700 km) autour de sa valeur moyenne (384 401 +/- 1 km).
 Objectifs
Objectifs Introduction
Introduction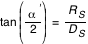
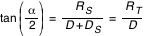 donc
donc 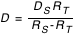
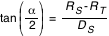 et comme
et comme 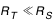
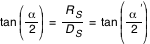
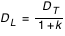 , en posant
, en posant 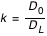 .
Or k est également égal au rapport du diamètre angulaire de l'ombre de la Terre (à la distance de la Lune) par le diamètre angulaire de la Lune, et peut être estimé observationnellement. Connaissant alors le diamètre absolu de la Lune et son diamètre apparent, il est aisé de calculer sa distance.
.
Or k est également égal au rapport du diamètre angulaire de l'ombre de la Terre (à la distance de la Lune) par le diamètre angulaire de la Lune, et peut être estimé observationnellement. Connaissant alors le diamètre absolu de la Lune et son diamètre apparent, il est aisé de calculer sa distance.










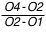 .
.
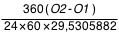 avec O2-O1 mesuré en minutes.
avec O2-O1 mesuré en minutes.
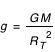 .
.
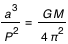 où a est la distance Terre-Lune et P est la période de rotation anomalistique de la Lune autour de la Terre (P=27,55 jours correspondant au temps écoulé entre deux passages au périgée).
où a est la distance Terre-Lune et P est la période de rotation anomalistique de la Lune autour de la Terre (P=27,55 jours correspondant au temps écoulé entre deux passages au périgée).