Mise en évidence de la rotation différentielle (niveau primaire ou première partie pour collège/lycée)
Nous pouvons procéder de différentes façons. La plus simple est d'utiliser un papier calque et de reproduire chaque tache en utilisant les photocopies du disques solaire jointes. On prendra soin de numéroter les jours d'observation et de les indiquer à cté de chaque tache.
Une fois que l'on aura décalqué les taches visibles sur les 12 photos du Soleil, on verra clairement le mouvement de chaque tache au cours du temps sur le calque. En regardant les positions extrêmes de deux taches prises à des latitudes différentes, on verra que la tache dont la latitude est la plus grande a "avancé" plus vite que l'autre.
Une autre manière de procéder est d'utiliser des diapositives et de les projeter sur un papier blanc ou, mieux, sur une demi-sphère blanche sur lesquels on dessinera les taches à chaque date d'observation.
Mesure de la vitesse de rotation du Soleil à différentes latitudes (niveau collège/lycée)
Nous allons maintenant mesurer la vitesse de rotation des taches et essayer de mettre en évidence la rotation différentielle du Soleil. Pour cela, il faut mesurer précisément la position des taches à plusieurs latitudes et à plusieurs époques.
Variation de la position des taches solaires sur 12 jours
| Numéro du cliché |
Date jj/mm/aa |
heure |
écart par rapport au 18/08/1990 à 00H00 |
longitude de la tache numéro |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
| 1 |
18/08/1990 |
15h32 |
0.647 jours |
|
|
|
|
|
|
|
|
| 2 |
19/08/1990 |
13h35 |
1.566 jours |
|
|
|
|
|
|
|
|
| 3 |
20/08/1990 |
10h08 |
2.422 jours |
|
|
|
|
|
|
|
|
| 4 |
21/08/1990 |
09h31 |
3.396 jours |
|
|
|
|
|
|
|
|
| 5 |
22/08/1990 |
08h01 |
4.334 jours |
|
|
|
|
|
|
|
|
| 6 |
23/08/1990 |
07h51 |
5.327 jours |
|
|
|
|
|
|
|
|
| 7 |
24/08/1990 |
06h56 |
6.289 jours |
|
|
|
|
|
|
|
|
| 8 |
25/08/1990 |
13h16 |
7.553 jours |
|
|
|
|
|
|
|
|
| 9 |
26/08/1990 |
08h35 |
8.358 jours |
|
|
|
|
|
|
|
|
| 10 |
27/08/1990 |
11h50 |
9.493 jours |
|
|
|
|
|
|
|
|
| 11 |
28/08/1990 |
09h53 |
10.412 jours |
|
|
|
|
|
|
|
|
| 12 |
29/08/1990 |
07h47 |
11.324 jours |
|
|
|
|
|
|
|
|
|
| latitude de la tache |
|
|
|
|
|
|
|
|
Choisir une belle tache que l'on peut suivre sur plusieurs jours. Mesurer, en interpolant dans la grille superposée au disque solaire, la latitude de la tache ainsi que sa longitude à différentes dates. Les porter dans le tableau 1. Recommencer pour d'autres taches à d'autres latitudes.
La vitesse de rotation Ω est définie par Ω = [d l / dt] ou l est la longitude. La période de rotation P est alors donnée par P = 360 / Ω. À partir des valeurs portées dans le tableau 1, on peut calculer la vitesse de rotation de plusieurs manières selon le niveau des élèves.
Première méthode
La manière la plus simple (pour le collège) consiste à prendre la différences des valeurs extrèmes de la longitude d'une tache et de la diviser par la durée séparant les taches. Par exemple, si la longitude d'une tache est -26,0 degrés le 18/08/1990 à 15h32 et 36,0 degrés le 23/08/1990 à 07h51, la vitesse de la tache est [36,0 - (-26,0)] / [5,327 - 0,647] = 13.24 °/jour ce qui donne une période de rotation de 27,2 jours.
Une estimation de l'erreur pourra être donnée si l'on connait l'incertitude sur les mesures individuelles de la longitude. Si, par exemple, on donne les longitudes à un demi degré près, l'incertitude sur la vitesse de rotation sera [2 x 0,5] / [5.327 - 0.647] = 0,2 °/jour. La période sera donc comprise entre [360 / (13.24 + 0,2)] et 360 / [13.24 - 0,2] c'est-à-dire entre 26,8 et 27,6 jours.
Deuxième méthode
Une deuxième méthode (toujours niveau collège) consiste à tracer sur du papier millimétré la latitude des taches en fonction de la date. Pour chaque tache, les points sont alignés et la pente de la droite est égale à la vitesse de rotation de la tache. À l'aide d'une règle, on peut tracer la droite reliant au mieux les points. En menant des parallèles aux axes horizontaux et verticaux, on peut tracer un triangle rectangle dont l'hypothénuse est un segment de la droite reliant les points. La pente de la droite est alors égale au rapport des deux ctés formant l'angle droit.
Troisième méthode
Une méthode plus précise (niveau lycée-prépa) consiste à effectuer une régression linéaire par moindre carrés. On utilise ainsi l'information sur toutes les observations d'une tache et on obtient également une estimation de la précision de la vitesse de rotation calculée.
Toutefois, les calculs, qui sont plus du niveau 1er cycle universitaire ou prépa que du niveau lycée peuvent être remplacés par l'utilisation des fonctions statistiques d'une calculatrice (que les élèves savent parfaitement utiliser au lycée).
Pour les braves, les équations (un peu compliquées) sont les suivantes :
Supposons que la longitude li (l1, l2, ... ln) d'une tache ait été observée n fois à des dates ti (t1, t2, ... tn) et on cherche à exprimer l comme une fonction affine de t
l = Ωt + t0, où Ω est la pente de la droite et t0 est une constante dépendant de l'origine des temps choisie. Le calcul par moindres carrés consiste à chercher Ω et t0 qui minimisent la somme des écarts quadratiques
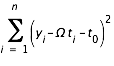 .
.
Calculons les sommes suivantes
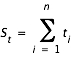
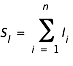
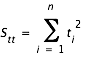
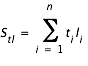
La pente de la droite est alors donnée par
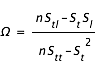
et la constante t0 est donnée par la formule
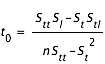
et une estimation 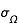 de l'erreur sur Ω est
de l'erreur sur Ω est
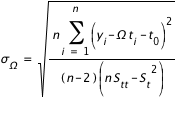
Résultats
Une fois que l'on a mesuré, par l'une des trois méthodes, la période de rotation du Soleil à différentes latitudes, on vérifiera que le Soleil tourne plus vite à l'équateur.
Les périodes trouvées varient de 27 jours environ à l'équateur à 30 jours environ à 60 degrés de latitude.

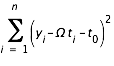 .
.
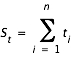
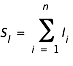
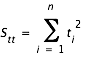
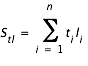
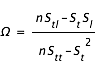
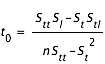
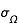 de l'erreur sur
de l'erreur sur