Champ: Système solaire
Niveau: *
Temps: 2 à 3 heures
 Objectifs
Objectifs
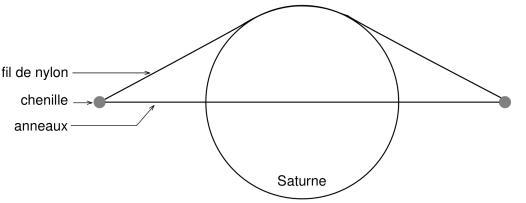
- Fabriquer une maquette à l'échelle de Saturne et de ses anneaux
- Expliquer comment les ombres se forment
- Comprendre comment la lumière se propage
 Prérequis
Prérequis
- Savoir utiliser la règle de 3.
- Pour les élèves les plus jeunes (niveau primaire), on pourra directement donner les tailles à utiliser.
- Pour le collège, une collaboration avec le professeur d'arts plastiques pour la construction de la maquette serait à envisager.
 Introduction
Introduction
Notre Soleil est une étoile vieille de 4,5 milliards d'années. Neuf planètes gravitent autour de lui : Mercure, Venus, la Terre, Mars, Jupiter, Saturne, Uranus, Neptune et Pluton. Mais la grande famille du système solaire ne s'arrête pas là. Il existe plus d'une centaines de satellites tournant autour de ces planètes, et plusieurs centaines de milliers de petits corps (comètes et astéroïdes) orbitant autour de notre étoile.
Sixième planète du Système Solaire, Saturne est la plus lointaine des planètes visibles à l'oeil nu (sa distance au Soleil est 9,5 fois la distance Terre - Soleil). Avec un diamètre 9,5 fois plus grand celui de la Terre, Saturne est la 2 ème plus grosse planète du système solaire, après Jupiter.
Elle possède de plus la particularité d'être entourée d'un spectaculaire système d'anneaux, identi- fiés par Huygens en 1659. Même s'ils ont l'air d'être pleins et continus, ils sont en réalité constitués de petits corps (composées essentiellement de glaces) situés sur des orbites différentes, et dont la taille varie de quelques centimètres à plusieurs mètres. L'origine de ces anneaux est encore mal connue. Ils résultent soit de la désagrégation de satellites qui se sont approchés trop près de la planète, soit de résidus du nuage primitif qui a donné naissance à tout le système solaire.
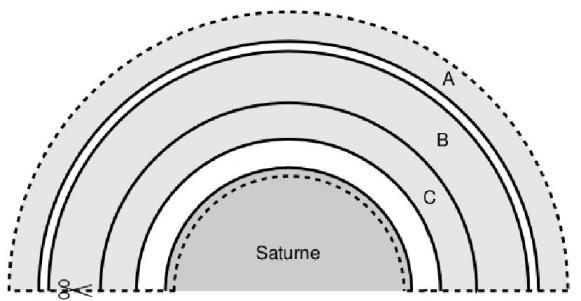
Depuis la Terre (cf. figure 2), on peut distinguer deux anneaux très brillants (notés A et B) séparés par la division Cassini, et un troisième plus sombre (C). Les sondes Voyager I et II, au début des années 1980, ont permis l'identification de 4 anneaux supplémentaires (D, le plus interne, et E, F, G, les plus externes). La figure 3 montre ces différents anneaux, et leur localisation. Finalement, le tableau 1 (ci-dessous) donne les caractéristiques de Saturne dont vous aurez besoin pour ce TP

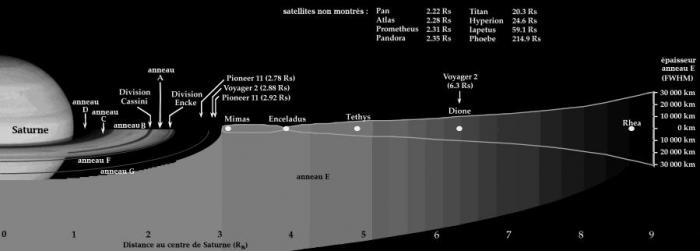
| nom de l'anneau | rayon interne | rayon externe |
|---|---|---|
| anneau E | 180 000 km | 480 000 km |
| anneau G | 165 800 km | 173 800 km |
| anneau F | 140 200 km | 140 700 km |
| anneau A | 122 000 km | 136 800 km |
| anneau B | 92 000 km | 117 500 km |
| anneau C | 74 500 km | 92 000 km |
| anneau D | 67 000 km | 64 500 km |
| rayon de Saturne | 60 500 km | |