Effet Dopler et vitesse radiale
Dans un système binaire, les corps suivent des ellipses dont un des foyers est occupé par le barycentre du système. Ainsi, la présence dune planète provoque autour de ce barycentre un mouvement de l'étoile centrale de même période de révolution P que la période de la planète (voir figure ci-dessous). En général, Mp<< M*, et on peut considérer que les orbites ont été circularisées par effet de marée. Le plan orbital faisant avec le plan du ciel un angle i (O < i < 90°), l'orbite est vue en projection sur le plan du ciel. L'observateur sur Terre ne voit que la vitesse radiale de l'étoile : vrad.
On mesure ainsi |vrad max|= v* . sin i. (Rq : si lorbite est elliptique, vrad n'est plus une fonction sinusoidale du temps et vmax ≠ vmin.
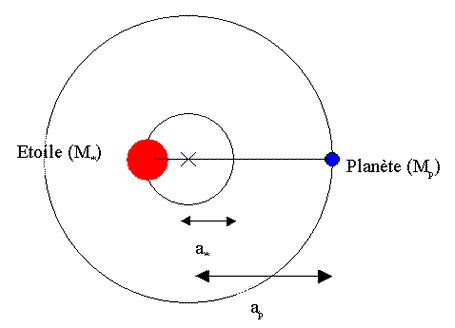
D'après la définition du barycentre, l'étoile parcourt donc une orbite de rayon a* = ap . Mp / M* Après avoir exprimé v* pour un mouvement circulaire de l'étoile, utiliser la 3ème loi de Kepler pour trouver l'expression de vrad max en fonction de M*, Mp, ap, sin i et G.
Calculer les vitesses radiales du Soleil engendrées par la présence de Jupiter et de la Terre, (on prendra i = 90°).
Une méthode spectroscopique de détection d'exoplanètes consiste à mesurer le décalage Doppler périodique des raies stellaires induit par le mouvement de l'étoile. Evaluer le formidable pouvoir de résolution (λ/Δλ) nécessaire pour atteindre les performances actuelles de 3m/s. En réalité, on n'a pas de tels pouvoirs de résolution, mais ils sont atteints en augmentant un pouvoir de résolution initial de 2-3 ordres de grandeur. Ceci grâce à l'étude simultanée d'un très grand nombre de raies.
Loi de Kepler
L'étoile HD209458 a la même luminosité que le Soleil, ce qui implique qu'elle est similaire à notre soleil, de même masse et de même rayon. En appliquant la troisième loi de Kepler, déterminer la taille de l'orbite de la planète, ap.
Masse de la planète
A partir de la relation trouvée en 1), retrouver la masse de la planète HD209458.
Probabilité dobserver un transit
Soit une planète en orbite circulaire de rayon ap autour de son étoile de rayon R*. La probabilité Ptransit dobserver un transit planétaire sécrit :
Calculer Ptransit dans le cas de Venus, la Terre, et Jupiter.
Retrouver la valeur de 1/10 trouvée dans le cas de la planète HD209458.
En déduire le rayon de la planète, puis sa densité et sa gravité à la surface.
Rayon de la planète
Soit L le flux de l'étoile de rayon R*. Trouver l'expression de la baisse de luminosité de létoile par rapport au flux total (ΔL / L), lors du transit d'une planète de rayon Rp. Dans le cas de l'étoile HD209458, on a mesuré une baisse de luminosité de 1,6 %.
Calculer pour comparaison, la chute de luminosité dans le cas de la Terre et de Jupiter.
En déduire le rayon de la planète, puis sa densité et sa gravité à la surface.