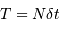SOLUTION

Avec les notations analogues au cours 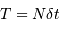$T = N \delta t$ , et en tenant compte des propriétés de la TF, on a :

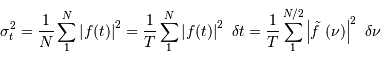
$\sigma_t^2 = {1\over N} \sum_1^N \left| f (t) \right|^{2} = {1\over T} \sum_1^N \left| f (t) \right|^{2} \ \delta t = {1\over T} \sum_1^{N/2} \left| \tilde f\ (\nu) \right|^{2} \ \delta \nu$

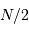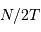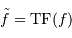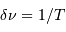en se servant de la relation de Perseval, et du fait que l'énergie est rapportée sur N/2 fréquences réelles entre les fréquences nulle et N/2T . Avec le changement de notation : $\tilde f = \mathrm{TF} (f)$ , et en tenant compte de $\delta \nu = 1/T$ :

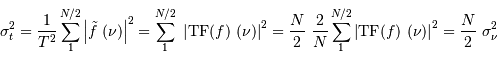
$\sigma_t^2 = {1\over T^2} \sum_1^{N/2} \left| \tilde f\ (\nu) \right|^{2} = \sum_1^{N/2}\ \left| \mathrm{TF} (f)\ (\nu) \right|^{2} = {N\over 2}\ {2\over N} \sum_1^{N/2} \left| \mathrm{TF} (f)\ (\nu) \right|^{2} = {N\over 2} \ \sigma_\nu^2$

On en déduit :

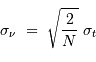
$\sigma_\nu\ =\ \sqrt{2\over N} \ \sigma_t$

Le bruit dans le spectre de Fourier diminue comme la racine carrée du nombre de points de mesure.