Intérêt de la transformée de Fourier
La TF permet la recherche de composantes périodiques dans un signal.
Les signaux ci-contre sont équivalents. L'un correspond à une série temporelle, l'autre à son spectre de Fourier.
Série temporelle et son spectre
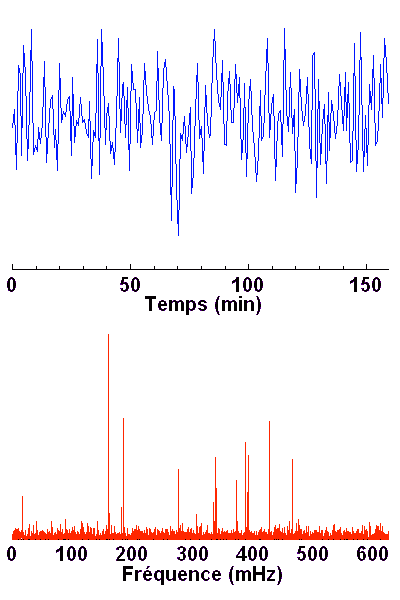
La série temporelle (extrait donné en bleu) ne montre rien de définissable. Son spectre de Fourier dévoile en revanche les fréquences propres qui constituent le signal, en les distinguant clairement du bruit.
Crédit : ASM
Exemple : signal sismique
L'astérosismologie est un sujet en plein développement, dont les observations se basent sur de longues séries temporelles, pour l'identification des modes propres d'oscillations dans le spectre de Fourier.
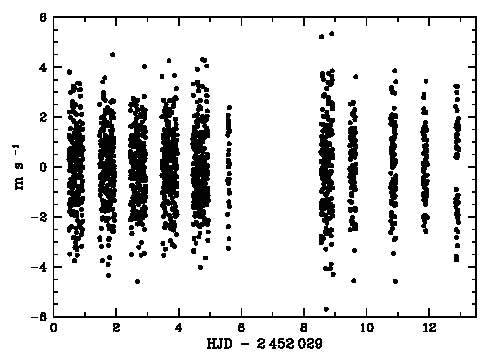
Série temporelle de données astérosismiques enregistrées à l'ESO, pendant 11 nuits, sur l'étoile
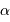
Cen.
Crédit : ESO
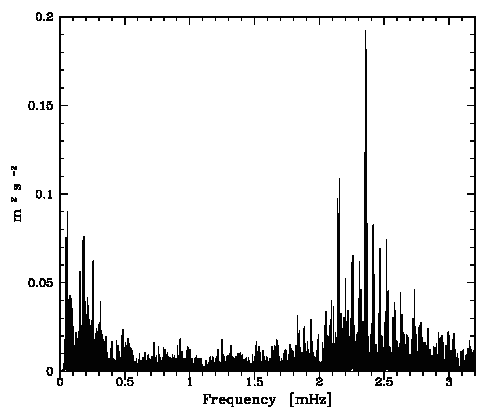
Spectre de Fourier de la série temporelle de données astérosismiques enregistrées à l'ESO, pendant 11 nuits, sur l'étoile alpha Cen.
Crédit : ESO
 Objectifs
Objectifs
Utiliser la TF pour la recherche de phénomènes périodiques.
Résolution en fréquence
Un signal observé durant une durée totale 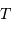 permet une résolution en fréquence
permet une résolution en fréquence 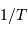 .
.
Fréquence de coupure
Un signal observé avec un échantillonnage 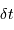 permet de suivre les fréquences jusqu'à la coupure
permet de suivre les fréquences jusqu'à la coupure 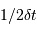 .
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
.
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
Echantillonnage
L'observation de phénomènes variables doit permettre :
- Un échantillonnage suffisamment rapide de la série temporelle, afin d'avoir accès aux variations les plus rapides.
- Une durée d'observation suffisamment longue pour suivre une période entière d'un phénomène périodique.
Résolution
Pour une série temporelle, la résolution en fréquence du spectre est d'autant meilleure que la base de temps d'observation est plus longue.
TF et résolution
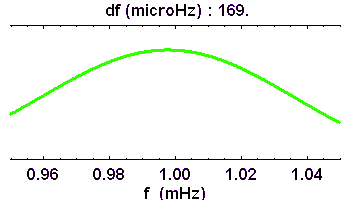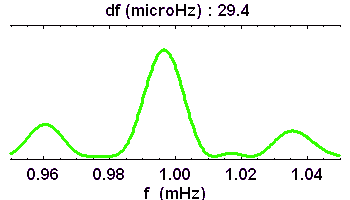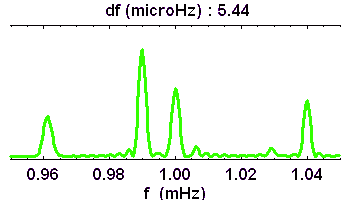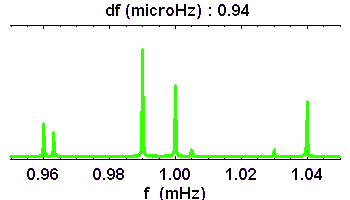
La résolution en fréquence, d'autant plus fine que la série temporelle initiale est longue, permet de dévoiler peu à peu la richesse du spectre.
Crédit : ASM
Pour une image, on relie la fréquence de coupure spatiale à la résolution spatiale .
TF et fréquence de coupure

M31, vue avec un nombre plus ou moins grand de fréquences spatiales (spectre de Fourier 2-D à gauche, image reconstruite à droite).
Crédit : ASM
 Pulsation de coupure
Pulsation de coupure
Difficulté : ☆☆
Temps : 30 min
On échantillonne un signal temporel avec un pas de temps 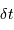 . On définit la pulsation
. On définit la pulsation 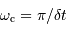 .
.
Question 1)
Montrer qu'il y a confusion entre les spectres de puissance des signaux périodiques de pulsation 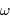 et
et
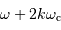 ou
ou 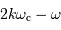 , où
, où 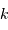 est un entier
est un entier
Courage, ce n'est qu'un peu de calculs sur les sinus.
Estimer 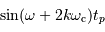 à une date
à une date 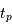 de l'échantillonnage
de l'échantillonnage
Supposer 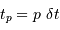
Question 2)
En déduire l'expression de la pulsation de coupure
Jusqu'à quelle fréquence n'y aura-t-il pas de confusion?


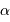 Cen.
Cen.

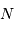 signaux, sur une durée totale
signaux, sur une durée totale 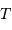 , l'analyse par transformée de Fourier se réécrit :
, l'analyse par transformée de Fourier se réécrit :
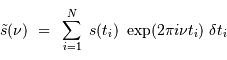
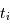 les dates individuelles et
les dates individuelles et 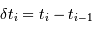 .
Si l'enregistrement est suffisamment régulier :
.
Si l'enregistrement est suffisamment régulier :
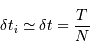
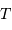 et
et 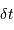 définissent les principales propriétés de l'analyse de Fourier.
définissent les principales propriétés de l'analyse de Fourier.
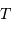 permet une résolution en fréquence
permet une résolution en fréquence 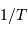 .
.
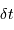 permet de suivre les fréquences jusqu'à la coupure
permet de suivre les fréquences jusqu'à la coupure 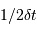 .
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
.
Le facteur 2 provient de la nécessité d'observer sur 2 mesures distinctes une demi-période négative et une demi-période positive.
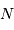 signaux, sur une durée totale
signaux, sur une durée totale 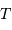 et avec un échantillonnage
et avec un échantillonnage 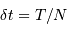 , on peut alors distinguer
sans ambiguïté
, on peut alors distinguer
sans ambiguïté 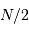 fréquences, entre
fréquences, entre 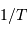 et
et 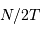 .
.


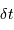 . On définit la pulsation
. On définit la pulsation 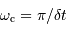 .
.
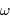 et
et
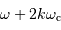 ou
ou 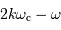 , où
, où 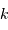 est un entier
est un entier
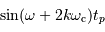 à une date
à une date 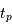 de l'échantillonnage
de l'échantillonnage
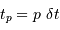
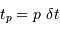 .
.
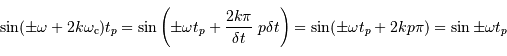
 ),
cette égalité est assurée à toute date de l'échantillonnage.
),
cette égalité est assurée à toute date de l'échantillonnage.
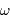 telles que
telles que
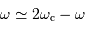 , càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.
, càd bien-sûr juste au voisinage supérieur de la fréquence de coupure.