Pourquoi filtrer un signal ?
Dans la chaîne de traitement du signal, des
observations brutes au résultat final, une étape souvent essentielle consiste à s'affranchir de signaux parasites. C'est possible lorsque ces derniers présentent des caractéristiques différentes de celles du signal, comme p.ex. un signal à basse fréquence qui contamine un signal sismique.
Analyse d'un signal sismique
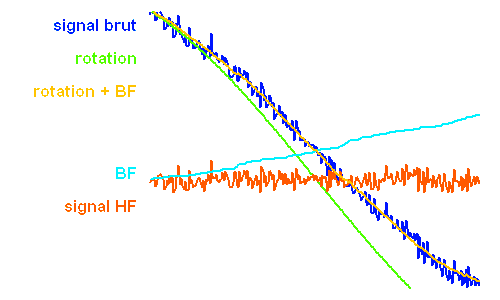
Le signal brut comprend plusieurs composantes. La rotation de la Terre, parfaitement modélisable, apporte une composante à basse fréquence (période de 24 h).
Un signal d'erreur, sur une source de référence, permet l'enregistrement d'une dérive également à basse fréquence. La correction de ces 2 termes ne comprend plus que des hautes fréquences, parmi lesquelles le signal sismique à analyser.
Crédit : ASM
Moyenne glissante
Un filtre par moyenne glissante substitue à une valeur donnée la moyenne des valeurs aux alentours, dans un intervalle de largeur 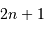 . Plus l'intervalle est grand, plus le filtrage est efficace.
. Plus l'intervalle est grand, plus le filtrage est efficace.
Ce filtrage présente des inconvénients que dévoile la transformée de Fourier.
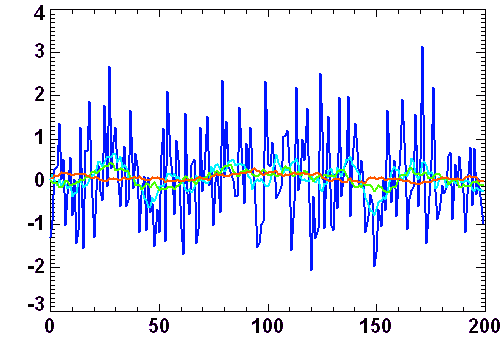
Moyennes glissantes, calculées localement sur 10 (bleu ciel), 20 (vert) ou 50 points (rouge).
Crédit : ASM
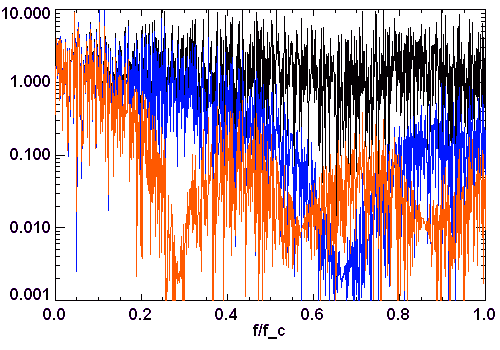
Spectre de Fourier (ordonnée en échelle logarithmique) d'une série de données non filtrée (courbe noire), ou filtrée par moyenne glissante de
sur un intervalle de largeur 3 (courbe bleue) ou 7 (courbe rouge). On s'aperçoit que le filtrage des fréquences par moyenne glissante est très irrégulier.
Crédit : ASM
Médiane
Un filtre par moyenne médiane substitue à une valeur donnée la médiane des valeurs aux alentours, dans un intervalle de largeur 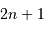 . Ce filtrage est efficace pour gommer les valeurs aberrantes.
. Ce filtrage est efficace pour gommer les valeurs aberrantes.
Moyennes médianes, calculées localement sur 10 (bleu ciel), 20 (vert) ou 50 points (rouge).
Crédit : ASM
Estimation linéaire
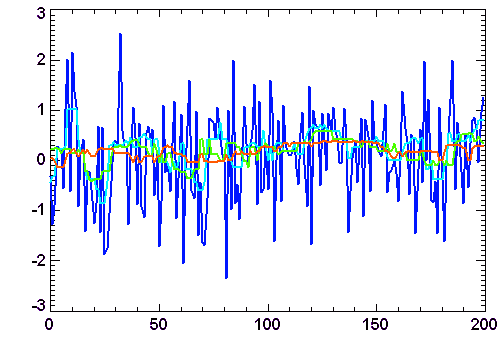
Réaliser une estimation linéaire d'une distribution de pont, c'est finalement ne décrire ce nuage de points que par 2 valeurs (ordonnée à l'origine et pente)
Estimation linéaire. Les hautes fréquences spatiales de la courbe rouge sont filtrées.
Crédit : ASM
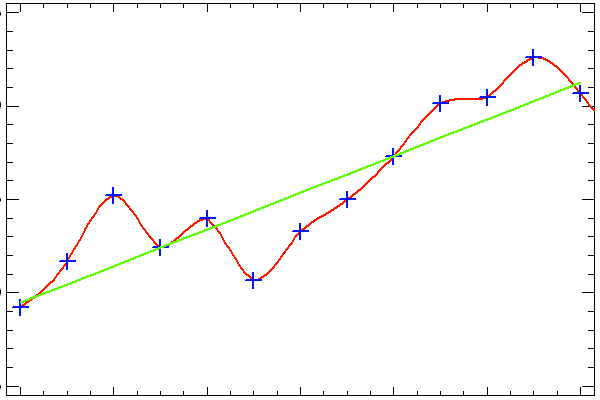
Traitement d'un point aberrant
La correction de valeurs aberrantes est typiquement une opération de filtrage. Un filtrage par moyenne glissante ou par la médiane n'y parvient pas avec la même efficacité.
La valeur aberrante est bien corrigée par le filtre médian (vert) mais pas par la moyenne glissante (bleu ciel)
Crédit : ASM
Filtrage en fréquence
Toute série de données, dépendant de quelque paramètre que ce soit (temps, variable d'espace, autre variable), à n'importe quelle dimension, peut être décrite par ses composantes fréquentielles.
Un filtrage ad hoc peut permettre de faire ressortir le signal des autres composantes.
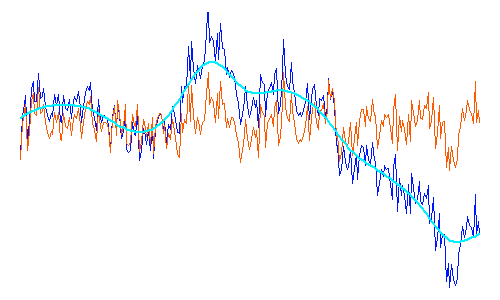
La correction par filtrage des basses fréquences (bleu ciel) permet de ne garder que le signal utile (rouge).
Crédit : ASM
 Prérequis
Prérequis
Analyse par transformée de Fourier
 Objectifs
Objectifs
Aborder quelques-uns des (nombreux) aspects de la transformée de Fourier.
Problématique
Il est souvent indispensable de séparer les différentes composantes en fréquences qui constituent une observation, pour extraire le signal de la contribution du bruit ou d'autres signaux, ce qui constitue un filtrage du signal.
Le but n'est pas de présenter sous forme de cours les multiples filtres possibles, mais plutôt quelques-uns de leurs effets.
Exemple de filtre temporel : l'acquisition de données
Toute acquisition de données, caractérisée par un pas de temps 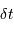 , filtre les fréquences temporelles plus rapides que
, filtre les fréquences temporelles plus rapides que 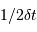 .
.
Filtrage par moyenne glissante
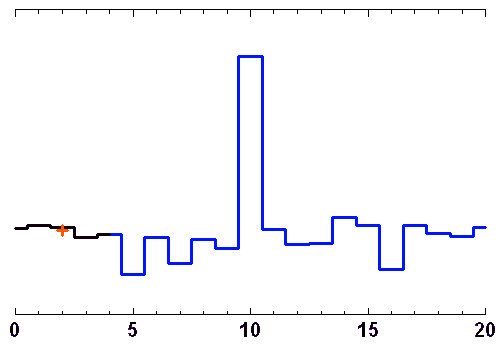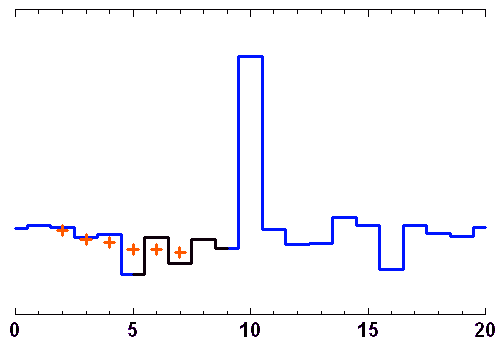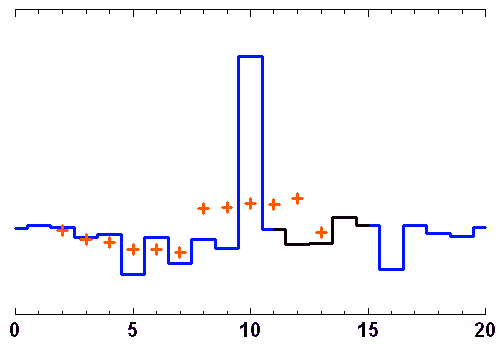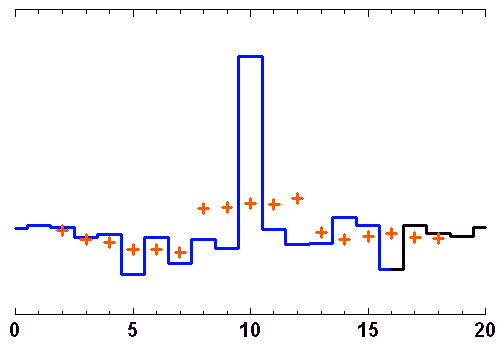
Un point donné est remplacé par la moyenne des points dans un intervalle centré autour de ce point, de plus ou moins ample largeur.
Crédit : ASM
Filtrage médian
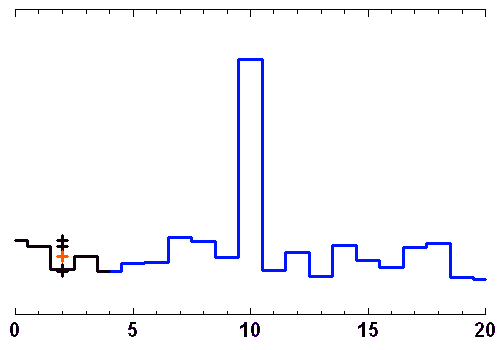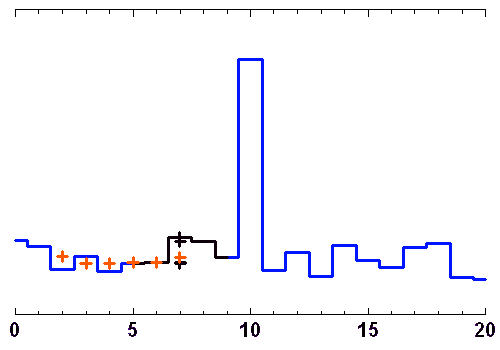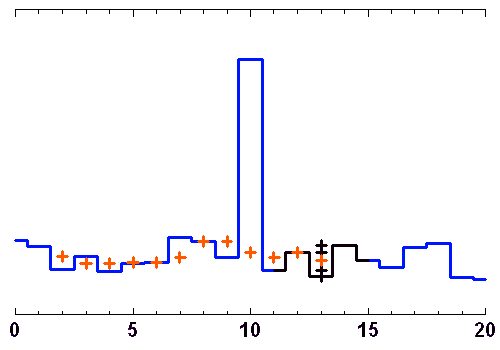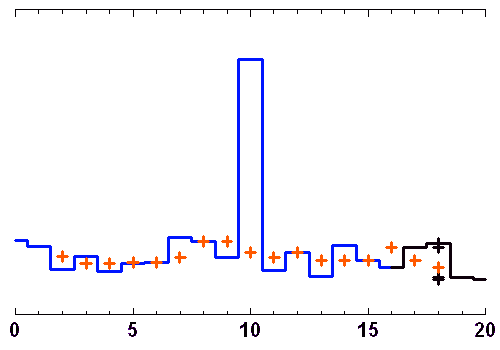
Un point donné est remplacé par la valeur médiane des points dans un intervalle centré autour de ce point, de plus ou moins ample largeur. Les points de chaque intervalle considéré ont été classés par valeur croissante, pour mettre en évidence la valeur médiane (indiquée en rouge).
Crédit : ASM
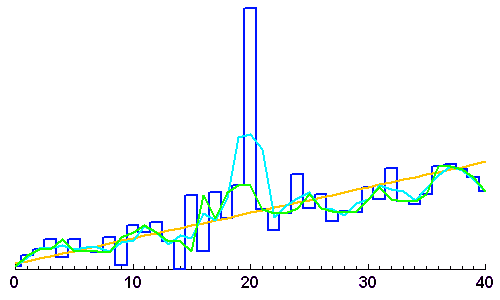
Filtrage par moyenne glissante

La série originale (en bleu) est filtrée par un filtre glissant, de largeur variable (en vert). Le nombre de points considérés pour la moyenne (en orange) a beau être de plus en plus élevé, le résultat (en rouge) présente toujours les oscillations originales, même lorsque la fenêtre est plusieurs fois plus large que la période du signal.
Crédit : ASM
Exemple de filtrage mal adapté
L'opération de filtrage n'est pas bégnine, et un filtre inadapté peut conduire à un mauvais résultat. Par exemple, le filtrage par moyenne glissante convient très mal pour un signal oscillant.
Exemple de filtrage numérique
La série temporelle ci-jointe est filtrée par filtrage numérique (algorithme de filtre à trous), avec séparation des hautes et basses fréquence. Les domaines de fréquence sont définis par rapport à une fréquence de valeur arbitraire ou mûrement réfléchie...
Filtrage numérique
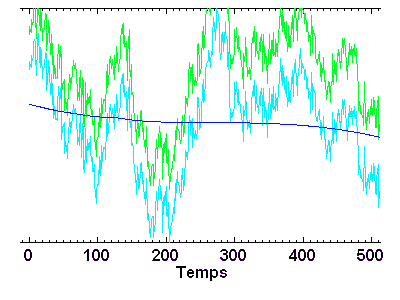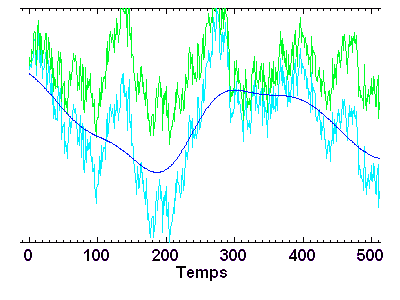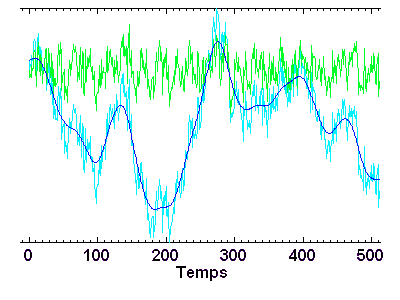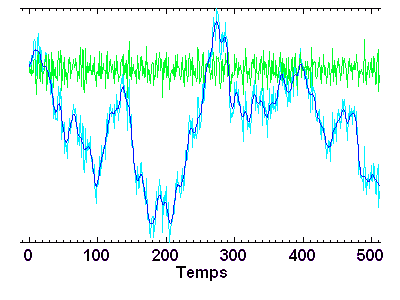
Filtrage d'un signal bruité (bleu ciel) en haute (vert) et basse (bleu foncé) fréquences, avec glissement progressif de la transition entre les définition de `haut' et `bas'.
Crédit : ASM
A la recherche de motifs
Les appliquettes ci-dessous dévoilent l'intérêt du filtrage. Elles représentent des cartes de Jupiter dans l'infrarouge thermique. Sans filtrage, c'est la structure en bandes parallèles à l'équateur qui domine l'image ; après filtrage de cette structure dominante, on voit apparaître des motifs de type ondulatoire, avec une dizaine de motifs répartis en longitude, couvrant une extension en latitude plus vaste que les bandes.
Utiliser les appliquettes pour dévoiler ces structures.



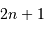 . Plus l'intervalle est grand, plus le filtrage est efficace.
. Plus l'intervalle est grand, plus le filtrage est efficace.


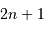 . Ce filtrage est efficace pour gommer les valeurs aberrantes.
. Ce filtrage est efficace pour gommer les valeurs aberrantes.




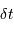 , filtre les fréquences temporelles plus rapides que
, filtre les fréquences temporelles plus rapides que 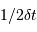 .
.
 par une ouverture
par une ouverture 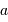 comme un filtrage des fréquences angulaires supérieures à
comme un filtrage des fréquences angulaires supérieures à 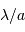 .
.




