La triangulation permet de mesurer des distances... à distance, la géométrie euclidienne rapportant à une mesure angulaire une mesure de distance.
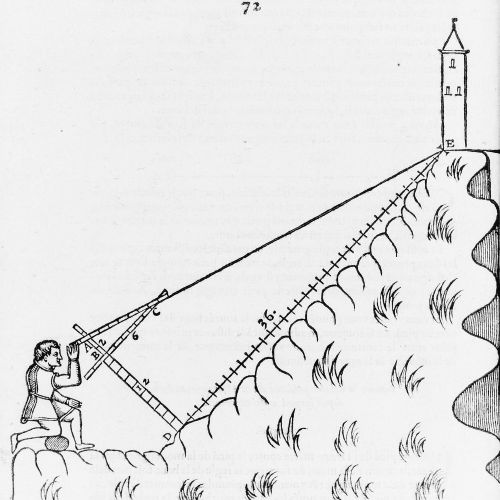
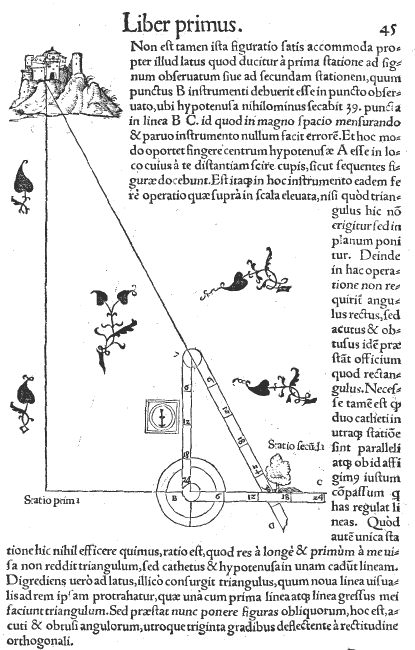
Mesurer une hauteur ou une distance ... à distance est souvent nécessaire, et nombreuses sont les illustrations mettant en pratique la mesure de distances par triangulation. Remarquer l'esthétique de ces représentations !
PrérequisRelations trigonométriques
Dans un
triangle de côtés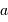 
, 
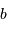et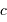 
et d'angles opposés 
, 
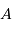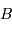et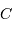 
, la relation du triangle s'énonce :
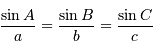
Il en découle que la mesure de seulement deux angles et d'un côté du triangle permet de calculer les autres côtés.
En effet, le 3e angle est alors connu, par la relation dans un triangle, en géométrie plane :
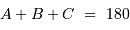
La relation liant côtés et angles permet alors de connaître la mesure de chaque côté.
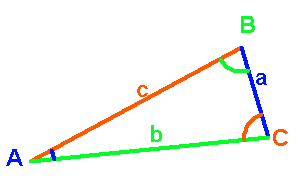
Si, p.ex, le côté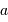 
est directement accessible à la mesure (p.ex. une distance sur Terre), ainsi que, que les angles 
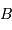et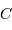 
, on a accès aux distances 
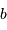et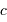 
(attention, les notations de la figure de principe sont différentes).
Incertitudes de mesureDifficulté : ☆ Temps : 15 min
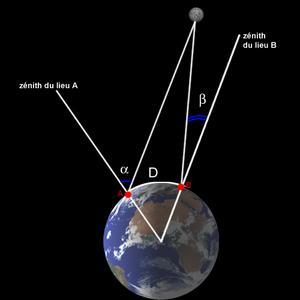
On mesure la parallaxe d'une étoile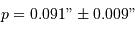 
.
A quelle distance est cette étoile ? Avec quelle précision ?
[2 points]
Le satellite européen HIPPARCOS a mesuré des parallaxes stellaires avec une précision moyenne de l'ordre de 1 mas (0.001 seconde d'arc). Jusqu'à quelle distance les mesures ont pu être obtenues avec une précision relative meilleure que 20% ?
[2 points]
Le projet GAIA doit atteindre une précision de l'ordre de 0.001 mas. Jusqu'à quelle distance pourra-t-on espérer la même précision relative ?
[1 points]
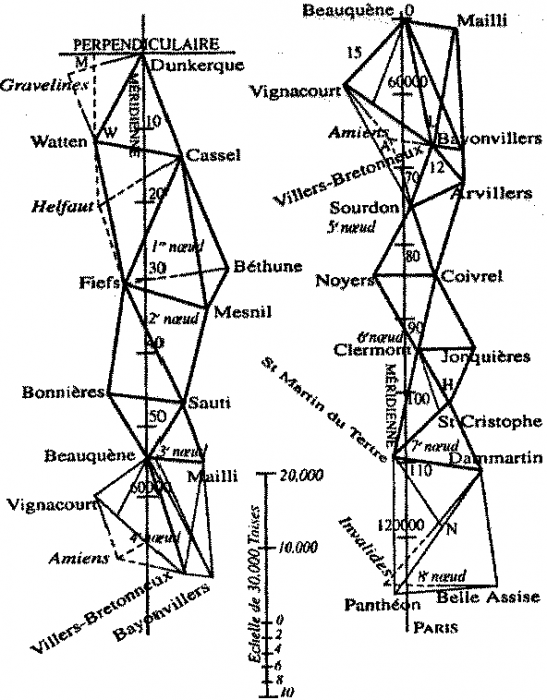
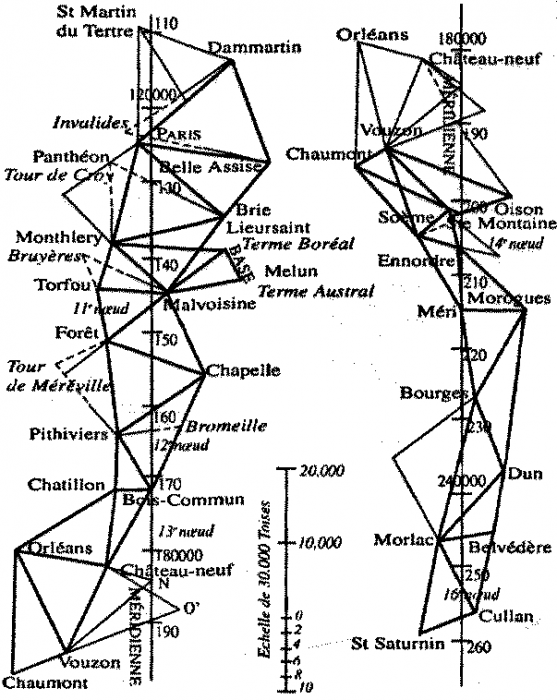
Par triangulation, les astronomes Delambre et Méchain ont mesuré la Terre, et défini le mètre, à la fin du XVIIIe siècle. Ils ont parcouru un arc de méridien, de Dunkerque à Barcelone, par une succession d'étapes formant des triangles juxtaposés. La mesure d'un seul des côtés d'un seul des triangles, la base, et de l'ensemble des angles a permis de déterminer la longueur de l'arc du méridien de Barcelone à Dunkerque, en passant par Paris.
L'extrapolation de la mesure du méridien, de l'équateur au pôle nord, a alors été effectuée. Par définition, la longueur de ce quart de méridien a été posée égale à 10 000 km, ou 10 millions de mètres. Le mètre est à la mesure du quart de méridien terrestre (aujourd'hui : le mètre est devenu une unité dérivée, définie à partir de la seconde et de la vitesse de la lumière).
Ce n'est donc pas un hasard si l'équateur mesure 40 000 km. Le léger résidu provient d'une meilleure mesure, ultérieure, de la figure de la Terre, la mesure du mètre étant définitivement figée.
L'importance de la mesure par triangulation se retrouve dans bien des thématiques.
C'est en opérant des triangulations astucieuses que Kepler a déterminé la nature de l'orbite de Mars, pour en dériver ses lois ; il lui fallut se positionner dans le bon référentiel, héliocentrique, et considérer différents événements à différentes dates pour conduire les mesures.
De manière plus moderne, c'est à une sorte de triangulation que se livrent les astrophysiciens pratiquant l' interférométrie pour mesurer de très petits diamètres angulaires : en élargissement la base d'observation, ils arrivent à retrouver l'information de la distance.
La mission Gaia , lancée fin 2013 développe le sens de la triangulation à l'échelle de notre Galaxie.
