Trianguler
Mesurer une hauteur ou une distance ... à distance est souvent nécessaire, et nombreuses sont les illustrations mettant en pratique la mesure de distances par triangulation. Remarquer l'esthétique de ces représentations !

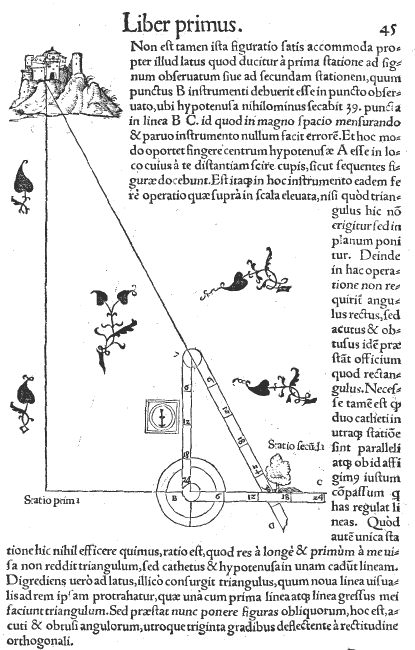
Mesurer une hauteur ou une distance ... à distance est souvent nécessaire, et nombreuses sont les illustrations mettant en pratique la mesure de distances par triangulation. Remarquer l'esthétique de ces représentations !


Relations trigonométriques
Dans un
triangle de côtés 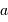 ,
, 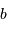 et
et 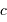 et d'angles opposés
et d'angles opposés 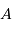 ,
, 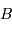 et
et 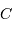 , la relation du triangle s'énonce :
, la relation du triangle s'énonce :
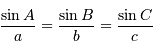
Il en découle que la mesure de seulement deux angles et d'un côté du triangle permet de calculer les autres côtés.
En effet, le 3e angle est alors connu, par la relation dans un triangle, en géométrie plane :
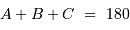
La relation liant côtés et angles permet alors de connaître la mesure de chaque côté.
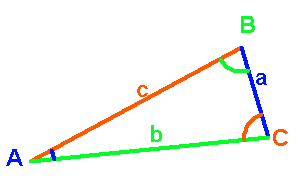
Si, p.ex, le côté 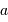 est directement accessible à la mesure (p.ex. une distance sur Terre), ainsi que, que les angles
est directement accessible à la mesure (p.ex. une distance sur Terre), ainsi que, que les angles 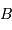 et
et 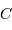 , on a accès aux distances
, on a accès aux distances 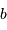 et
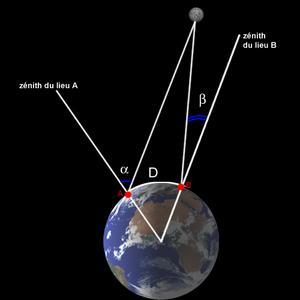
et 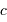 (attention, les notations de la figure de principe sont différentes).
(attention, les notations de la figure de principe sont différentes).
Difficulté : ☆ Temps : 15 min
On mesure la parallaxe d'une étoile 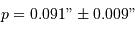 .
A quelle distance est cette étoile ? Avec quelle précision ?
.
A quelle distance est cette étoile ? Avec quelle précision ?
[2 points]
Le satellite européen HIPPARCOS a mesuré des parallaxes stellaires avec une précision moyenne de l'ordre de 1 mas (0.001 seconde d'arc). Jusqu'à quelle distance les mesures ont pu être obtenues avec une précision relative meilleure que 20% ?
[2 points]
Le projet GAIA doit atteindre une précision de l'ordre de 0.001 mas. Jusqu'à quelle distance pourra-t-on espérer la même précision relative ?
[1 points]