Les différentes phases de l'univers
Auteurs: Sylvain Fouquet, François Hammer
- Introduction
- Les particules sub-atomiques
- Exercices
- L'antimatière
- Création de particules élémentaires
- Exercices de physique subatomique
- Terra incognita - l'ère quantique
- L'ère hadronique
- l'ère leptonique
- L'ère radiative
- L'ère stellaire
- Résumé
Introduction
Les sections précédentes ont décrit trois résultats concrets et observables du modèle du Big Bang, un univers en expansion, le Fond Diffus Cosmologique et les proportions d'hydrogène et d'hélium de notre univers. Ces trois phénomènes sont de puissants arguments en faveur du modèle du Big Bang. Par la suite, les différentes étapes de l'univers seront décrites dans le cadre du Big Bang, des premières millièmes de secondes jusqu'à nos jours. L'univers y est décrit comme une fournaise primordiale composée d'éléments subatomiques mélangés interagissant fortement avec la lumière. Cet univers, du fait de son expansion, se refroidit rapidement permettant la création d'éléments plus complexes tels que des protons, des neutrons et ensuite des noyaux d'hydrogène et d'hélium. Après 380 000 ans, la lumière et la matière se découplent enfin, laissant un univers composé de 75% d'atomes d'hydrogène et 25% d'atomes d'hélium. Cet univers qui est devenu froid et neutre rentre dans l'âge sombre et connaîtra, des centaines de millions d'années plus tard, une phase de réionisation où le gaz neutre deviendra ionisé. La dernière grande étape de l'univers qui dure plus de 13 milliards d'années correspond à la formation et surtout à l'évolution des étoiles et des galaxies.
Formation des structures de l'univers
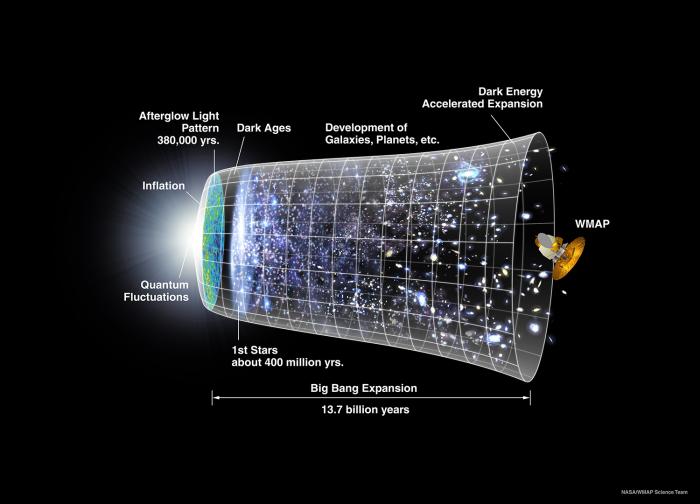
Résumé des différentes étapes de structuration de l'univers depuis le Big Bang à nos jours : le Big Bang, la recombinaison, l'âge sombre, la réionisation, la structuration de l'univers.
Crédit :
La mission
WMAP.
Les particules sub-atomiques
Dans ses premiers instants, l'univers s'apparente à un plasma de particules élémentaires qui interagissent entre elles et avec la lumière, formant un système à l'équilibre. Des connaissances sur la physique des particules est alors primordiale pour comprendre ces premiers instants. L'expansion de l'univers ne remet pas en cause cet état d'équilibre mais oblige la matière à passer d'un état en équilibre à un autre. Les premiers instants de l'univers sont l'unique moment où l'univers connaît des températures de plusieurs milliards de Kelvin et des densités de plusieurs milliards de fois celle de l'eau. Bien que l'homme ait construit des accélérateurs de particules pour reproduire des chocs très énergétiques similaires à ceux du début de l'univers pour obtenir des particules subatomiques, il n'accède pas encore aux énergies des tous premiers instants (les premières 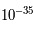 secondes).
secondes).
Par la suite, nous utiliserons une nouvelle unité pour la masse des particules. Cela tient au fait que leurs masses sont si faibles que la notation en kg est assez lourde et peu parlante. Par la suite, les masses seront données en eV (électron-Volt), qui est une unité d'énergie. Chaque masse peut être considérée comme une énergie par la formule d'équivalence 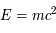 . La conversion de la masse en énergie qui en découle donne des Joules, l'unité standard. Puis, cette énergie est convertie en eV (électron-Volt, énergie que gagne un électron dans un champs de 1 Volt en une seconde) par la relation suivante : 1 eV =
. La conversion de la masse en énergie qui en découle donne des Joules, l'unité standard. Puis, cette énergie est convertie en eV (électron-Volt, énergie que gagne un électron dans un champs de 1 Volt en une seconde) par la relation suivante : 1 eV = 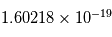 J. Par exemple, un proton ayant une masse de
J. Par exemple, un proton ayant une masse de 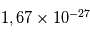 kg a une énergie de
kg a une énergie de 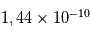 J qui équivaut à 900 MeV (Mega-eV).
J qui équivaut à 900 MeV (Mega-eV).
De même, pour parler de l'énergie d'un photon, on sera amené à utiliser l'énergie propre d'un photon donnée par la relation 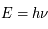 , où
, où 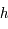 est la constante de Planck
est la constante de Planck 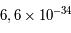 J.s et
J.s et 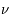 la fréquence du photon mais aussi l'énergie statistique moyenne des photons qui découle de la loi de Wien. Pour une température donnée, l'énergie des photons se situe au alentour du pic du corps noir. En moyenne, un photon, dans un corps noir d'une température de
la fréquence du photon mais aussi l'énergie statistique moyenne des photons qui découle de la loi de Wien. Pour une température donnée, l'énergie des photons se situe au alentour du pic du corps noir. En moyenne, un photon, dans un corps noir d'une température de 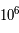 K, aura, d'après la loi de Wien, une longueur d'onde de 2,9 nm ce qui correspond à une énergie de
K, aura, d'après la loi de Wien, une longueur d'onde de 2,9 nm ce qui correspond à une énergie de 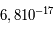 J ou 426 eV.
J ou 426 eV.
Enfin, pour les particules, on peut parler de l'énergie cinétique d'une particule, 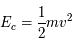 où
où 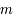 est sa masse et
est sa masse et 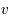 sa vitesse. On peut aussi dans le cas d'un corps noir parler d'énergie statistique des particules reliant leurs vitesses et la température du corps noir :
sa vitesse. On peut aussi dans le cas d'un corps noir parler d'énergie statistique des particules reliant leurs vitesses et la température du corps noir : 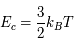 où
où 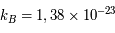 m2.kg.s-2.K-1 est la constante de Boltzmann et
m2.kg.s-2.K-1 est la constante de Boltzmann et 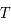 la température du corps noir. En moyenne, un proton dans un plasma de corps noir à la température de
la température du corps noir. En moyenne, un proton dans un plasma de corps noir à la température de 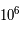 K aura une énergie cinétique égale à
K aura une énergie cinétique égale à 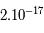 J = 129 eV qui correspond à une vitesse de 160 km/s.
J = 129 eV qui correspond à une vitesse de 160 km/s.
Les hadrons
Liste des particules subatomiques

Classement des particules subatomiques en fonction de leur familles : photon, lepton et hadron.
Tableau des particules élémentaires
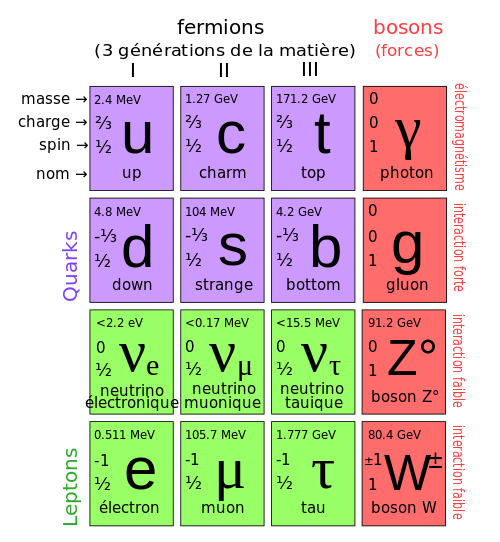
Tableau des particules élémentaires d'après le modèle standard. On y retrouve la famille des leptons. Les photons appartiennent à la famille des bosons avec le gluon et les bosons Z et W. Les six quarks sont les particules élémentaires dont les combinaisons forment les hadrons.
Les hadrons forment la famille de particules subatomiques la plus riche. Elle compte des représentants très connus tel que le proton et le neutron (les nucléons), mais aussi une flopée de particules instables qui ne s'observent qu'assez rarement. Parmi elles se trouve la sous famille des mésons (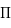 ,
, 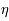 , ...), ou celle des hypérons (
, ...), ou celle des hypérons (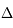 ,
, 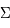 , ...). Le schéma ci-joint résume clairement ces différentes familles. Les hadrons forment une structure complexe car ce ne sont pas des particules élémentaires. Elles sont elle-mêmes l'association de particules élémentaires, les quarks, jusqu'à preuve du contraire. Par exemple, le proton est l'assemblage de trois quarks : deux quarks up et un quark down. A l'inverse, le neutron est constitué de deux quarks down et d'un quark up. Les hadrons ont une masse, une charge et un spin. Ils peuvent donc ressentir les interactions gravitationnelles et électromagnétiques sauf si leur charge est nulle comme pour le neutron. En plus de cela, ils sont sujets par définition à l'interaction forte et faible. A chaque hadron est associé un nombre hadronique. Par exemple, le neutron et le proton ont un nombre hadronique de 1. Ce nombre doit être conservé dans une transformation tout comme est conservée la charge électrique.
, ...). Le schéma ci-joint résume clairement ces différentes familles. Les hadrons forment une structure complexe car ce ne sont pas des particules élémentaires. Elles sont elle-mêmes l'association de particules élémentaires, les quarks, jusqu'à preuve du contraire. Par exemple, le proton est l'assemblage de trois quarks : deux quarks up et un quark down. A l'inverse, le neutron est constitué de deux quarks down et d'un quark up. Les hadrons ont une masse, une charge et un spin. Ils peuvent donc ressentir les interactions gravitationnelles et électromagnétiques sauf si leur charge est nulle comme pour le neutron. En plus de cela, ils sont sujets par définition à l'interaction forte et faible. A chaque hadron est associé un nombre hadronique. Par exemple, le neutron et le proton ont un nombre hadronique de 1. Ce nombre doit être conservé dans une transformation tout comme est conservée la charge électrique.
Les leptons
Les leptons sont de vraies particules élémentaires pour autant que l'on sache. Les leptons les plus connus sont l'électron et le neutrino, découvert plus récemment. Ils ont une masse, même le neutrino qui auparavant était jugé sans masse, et peuvent aussi être chargés. Ils ont un nombre leptonique qui à l'instar du nombre hadronique est constant dans les réactions nucléaires. Par exemple, l'électron et le neutrino électronique, 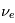 , ont un nombre leptonique de 1.
, ont un nombre leptonique de 1.
Les photons
Les photons sont les premières particules élémentaires connues. Elles nous entourent et sans elles le monde serait invisible pour l'homme. Elles ont la particularité de ne pas avoir de masse, ni de charge mais un spin de valeur 1. Elles font partie de la famille des bosons.
Exercices
 Grandeurs caractéristiques
Grandeurs caractéristiques
Question 1)
Quel est la masse en MeV de l'Uranium 235 et de l'Uranium 238 ?
Question 2)
Pour un plasma à une température 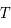 , la vitesse moyenne d'une particule vaut :
, la vitesse moyenne d'une particule vaut :
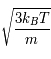
où 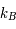 est la constante de Boltzmann,
est la constante de Boltzmann, 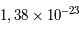 m2.kg.s-2.K-1,
m2.kg.s-2.K-1, 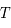 la température en Kelvin et m la masse en kg. Quelle est la vitesse d'un proton à 3 000 K et à 3x109 K ? Vérifier que nous sommes bien dans un régime classique et non relativiste.
la température en Kelvin et m la masse en kg. Quelle est la vitesse d'un proton à 3 000 K et à 3x109 K ? Vérifier que nous sommes bien dans un régime classique et non relativiste.
Question 3)
Soit l'électron de masse 0,511 MeV, à quelle température la collision de deux neutrons pourrait donner un couple électron-positron en plus des deux neutrons de base ?
Question 4)
Quel photon a l'énergie de masse d'un proton ?
L'antimatière
Propriétés de l'antimatière
L'antimatière, contrairement à ce que son nom indique, est de la matière dans le sens où elle a une masse, une charge, un spin, etc, comme la matière classique. Le suffixe "anti" met en exergue le fait que chaque particule de matière que l'on connaît a un jumeau d'antimatière ayant la même masse mais dont toutes les autres grandeurs sont opposées. Par exemple, la particule d'antimatière la plus connue et utilisée à ce jour est sans doute le positron, l'anti-électron ou électron positif. Le positron a la même masse que l'électron mais sa charge est positive, d'où son nom. Cette inversion vaut aussi pour le nombre leptonique qui passe de +1 pour l'électron à -1 pour le positron. De même, le neutron a son anti-neutron et le proton son anti-proton, etc. Le photon a la particularité d'être sa propre anti-particule.
L'antimatière dans notre univers
Où est l'antimatière ? A l'état naturel, l'antimatière s'observe au cours de la désintégration dite 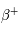 qui transforme un proton en neutron et libère un positron. Cette désintégration intervient au sein des noyaux atomiques dans la matière dite radioactive comme l'Uranium 235. Les rayons cosmiques peuvent aussi générer des anti-particules. En effet, ces derniers sont des particules provenant de l'espace et ayant une grande énergie cinétique, donc une vitesse proche de celle de la lumière. Ce sont souvent des protons. En pénétrant dans l'atmosphère, ils rentrent en collision avec des particules de gaz et forment une gerbe de particules contenant des anti-particules. Historiquement, le positron fut découvert à la suite d'un rayon cosmique. Les accélérateurs de particules sont un autre moyen de créer des anti-particules. Le principe est le même que pour les rayons cosmiques sauf que c'est un accélérateur de particules créé par l'homme qui accélère un proton grâce à de puissants champs magnétiques et le fait collisionner dans une immense chambre pour étudier avec précision les particules résultantes de la collision. Néanmoins, exceptés ces trois processus, l'univers semble dépourvu d'antimatière. En effet, au contact de la matière, l'antimatière s'annihile pour former des photons très énergétiques. Si une partie de notre univers était faite d'antimatière nous devrions voir la limite avec la zone de matière par un dégagement de lumière intense, or il n'en est rien. On peut toujours rêver à une zone de l'univers si bien isolée et éloignée de nous que l'antimatière aurait survécu, mais cela est de plus en plus improbable.
qui transforme un proton en neutron et libère un positron. Cette désintégration intervient au sein des noyaux atomiques dans la matière dite radioactive comme l'Uranium 235. Les rayons cosmiques peuvent aussi générer des anti-particules. En effet, ces derniers sont des particules provenant de l'espace et ayant une grande énergie cinétique, donc une vitesse proche de celle de la lumière. Ce sont souvent des protons. En pénétrant dans l'atmosphère, ils rentrent en collision avec des particules de gaz et forment une gerbe de particules contenant des anti-particules. Historiquement, le positron fut découvert à la suite d'un rayon cosmique. Les accélérateurs de particules sont un autre moyen de créer des anti-particules. Le principe est le même que pour les rayons cosmiques sauf que c'est un accélérateur de particules créé par l'homme qui accélère un proton grâce à de puissants champs magnétiques et le fait collisionner dans une immense chambre pour étudier avec précision les particules résultantes de la collision. Néanmoins, exceptés ces trois processus, l'univers semble dépourvu d'antimatière. En effet, au contact de la matière, l'antimatière s'annihile pour former des photons très énergétiques. Si une partie de notre univers était faite d'antimatière nous devrions voir la limite avec la zone de matière par un dégagement de lumière intense, or il n'en est rien. On peut toujours rêver à une zone de l'univers si bien isolée et éloignée de nous que l'antimatière aurait survécu, mais cela est de plus en plus improbable.
Création de particules élémentaires
Disparition de l'antimatière
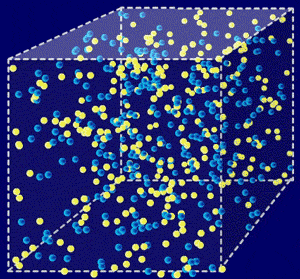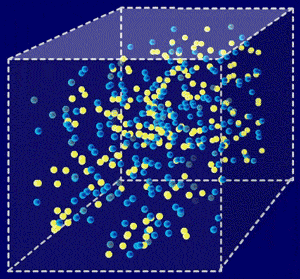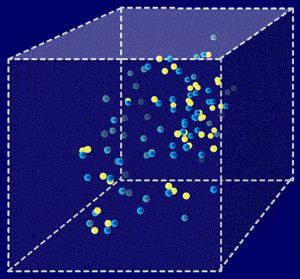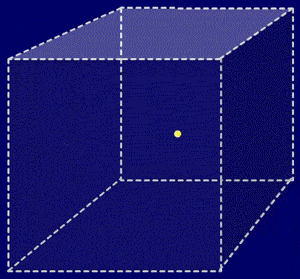
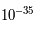
seconde après le Big Bang, l'Univers contenait des nombres de particules (représentées par des points jaunes) et d'antiparticules (en bleu) proches, mais avec un nombre très légèrement plus grand de particules. Cette animation montre le processus d'annihilation des particules et d'antiparticules. Cependant, il subsiste le léger déséquilibre entre particules et antiparticules.
Crédit :
ASM/Florence Durret, Fabienne Casoli et Gilles Bessou
Création de particules élémentaires
Comment créer des particules élémentaires ? La manière de créer des particules subatomiques est liée à la relation la plus célèbre de la physique 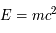 , où
, où 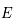 est l'énergie de masse d'une particule,
est l'énergie de masse d'une particule, 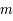 sa masse et
sa masse et 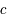 la vitesse de la lumière. Cette relation nous dévoile le fait qu'il existe une équivalence entre matière et énergie. Il est alors possible de transformer l'une en l'autre. Cependant, comme dans une réaction nucléaire, la charge, le nombres baryonique et leptonique doivent être conservés, donc cela interdit certaines réactions. Par exemple, la réaction suivante :
la vitesse de la lumière. Cette relation nous dévoile le fait qu'il existe une équivalence entre matière et énergie. Il est alors possible de transformer l'une en l'autre. Cependant, comme dans une réaction nucléaire, la charge, le nombres baryonique et leptonique doivent être conservés, donc cela interdit certaines réactions. Par exemple, la réaction suivante :
proton 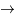 neutron + électron
neutron + électron
ne conserve pas la charge (+1 avant, -1 après), ni le nombre leptonique (0 avant, 1 après).
Lorsqu'une anti-particule rencontre une particule, les deux se transforment en photons, il y a annihilation de la matière. En revanche, lorsque deux photons collisionnent, il peut se former une particule et son anti-particule à condition que les photons aient une énergie totale supérieure à l'énergie de masse des particules créées. Par exemple, pour créer une paire électron-positron, d'énergie deux fois 0,511 Mev, il faut des photons d'une énergie totale de plus de 0,511 Mev, c'est à dire ayant une longueur d'onde d'au moins 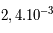 nm, soit des rayons gamma. Le rayonnement visible (400-800 nm) est bien trop faible énergétiquement pour créer des particules élémentaires.
nm, soit des rayons gamma. Le rayonnement visible (400-800 nm) est bien trop faible énergétiquement pour créer des particules élémentaires.
D'un autre côté, des chocs très énergétiques peuvent aussi créer de nouvelles particules. Ce phénomène physique est utilisé dans les collisionneurs de particules au CERN (Conseil européen pour la Recherche nucléaire). Ce processus requiert des conditions extrêmes. Créer une paire électron-positron exige des températures de plusieurs milliards de Kelvin donc des vitesses proches de celle de la lumière. Par comparaison, les températures atteintes au centre des étoiles ne sont que de quelques centaines de millions de Kelvin.
Comprendre la disparition de l'antimatière
Si la création d'une particule entraîne celle d'une anti-particule et si leur destruction est aussi symétrique, comment expliquer la prédominance des particules sur les anti-particules ? Ce problème reste à ce jour mal compris et sans réelle réponse. Une possible piste serait que certaines réactions nucléaires, plus compliquées que la simple collision de deux photons, aient créé une dissymétrie rendant prédominante la matière sur l'antimatière. Cela se serait passé dans les tous premiers instants de l'univers.
Exercices de physique subatomique
Auteur: Sylvain Fouquet
 Les nombres quantiques
Les nombres quantiques
Question 1)
Sachant que le proton est constitué de deux quarks u et d'un quark d et que le neutron est constitué de deux quarks d et d'un quark u, donnez la charge du quark u et d.
Question 2)
Le méson pion 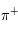 est constitué d'un quark
est constitué d'un quark 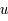 et d'un antiquark
et d'un antiquark 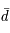 . Quelle est sa charge ? Quelle est son antiparticule et la charge de celle-ci ?
. Quelle est sa charge ? Quelle est son antiparticule et la charge de celle-ci ?
Auteur: Sylvain Fouquet
 Désintégration du neutron
Désintégration du neutron
Difficulté : ☆☆☆
Question 1)
Lorsque un neutron est à l'état libre, il est instable et se transforme en proton. Dans un noyau, il devient stable. Son temps de désintégration est de 885,7 s soit près de 15 min. Il se désintègre en un proton, un électron et un antineutrino électronique.
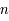
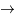
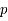 +
+ 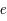 +
+ 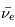
Vérifier que la charge, le nombres baryonique et le nombre leptonique sont conservés.
Question 2)
Une fois que le neutron s'est désintégré, les trois particules résultantes prennent des directions différentes. Il est possible de détecter le proton et l'électron mais le neutrino n'interagit quasiment pas avec la matière. Arrêter la moitié d'un flux de neutrinos requiert un mur d'une année lumière de plomb. Comment montrer alors son existence sans recourir à l'argument de la conservation du nombre leptonique ?
Terra incognita - l'ère quantique
La théorie du Big Bang s'attache à décrire l'univers depuis ses premiers instants. Plus on remonte dans le passé, plus l'univers est dense et chaud. En théorie, la température et la densité croissent de manière infinie jusqu'au temps zéro. Cela crée un univers avec des conditions que nous n'avons jamais rencontrées sur terre et que nous n'avons jamais reproduites dans un accélérateur de particules. Cette époque de l'univers, les 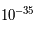 premières secondes, sont terra incognita.
premières secondes, sont terra incognita.
Cela n'empêche pourtant pas les chercheurs d'échafauder de nombreuses théories pour expliquer cette époque de l'univers. Il en est même qui tentent d'expliquer ce qu'il y avait avant le Big Bang. Ce processus est normal en science, mais seule la contrainte observationnelle pourra trancher entre les différentes théories : théorie des supercordes, M-cordes, gravitation quantique, grande unification des lois fondamentales. C'est à cette époque de l'univers que pourrait avoir eu lieu l'inflation qui permet d'expliquer la grande homogénéité du FDC. En une fraction de seconde, l'univers se serait étendu d'un facteur 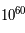 faisant passer des inhomogénéités sur des échelles microscopiques à des échelles macroscopiques. C'est aussi à la fin de cette époque que les quarks se seraient assemblés pour former les hadrons : muons, protons, neutrons, ...
faisant passer des inhomogénéités sur des échelles microscopiques à des échelles macroscopiques. C'est aussi à la fin de cette époque que les quarks se seraient assemblés pour former les hadrons : muons, protons, neutrons, ...
Tout cela est encore une terra incognita. Il faut des instruments plus performants pour créer des conditions de température et de pression qui avoisinent celles de l'univers durant les 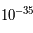 premières secondes. Le Large Hadron Collider (LHC large collisionneur d'hadron) devrait donner des pistes en produisant des énergies de l'ordre du Tev (
premières secondes. Le Large Hadron Collider (LHC large collisionneur d'hadron) devrait donner des pistes en produisant des énergies de l'ordre du Tev (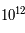 eV) ce qui correspond à une température de l'ordre de
eV) ce qui correspond à une température de l'ordre de 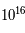 K.
K.
L'ère hadronique
l'ère leptonique
Entre les température 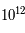 K et
K et 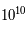 K, pendant un peu plus d'une seconde, l'univers se situe dans l'ère leptonique. La température de seuil des hadrons n'est plus atteinte. Les hadrons et leurs anti-particules se sont annihilés pour la plupart. Du fait d'une très légère dissymétrie avant l'annihilation, quelques hadrons ont survécu, un sur un milliard en ordre de grandeur. Il ne reste alors que des protons et des neutrons. L'univers est rempli de photons, de neutrinos, d'anti-neutrinos, d'électrons et de positrons. Le rapport entre les hadrons et les autres composantes est de 1 pour 1 milliard à peu près. Il y a presque autant de neutrinos, d'antineutrinos, d'électrons et de positrons. Des réactions incessantes se produisent, changeant protons en neutrons et vice-versa. Cependant, l'égalité du nombre des leptons assure l'égalité entre la proportion de neutrons et de protons.
K, pendant un peu plus d'une seconde, l'univers se situe dans l'ère leptonique. La température de seuil des hadrons n'est plus atteinte. Les hadrons et leurs anti-particules se sont annihilés pour la plupart. Du fait d'une très légère dissymétrie avant l'annihilation, quelques hadrons ont survécu, un sur un milliard en ordre de grandeur. Il ne reste alors que des protons et des neutrons. L'univers est rempli de photons, de neutrinos, d'anti-neutrinos, d'électrons et de positrons. Le rapport entre les hadrons et les autres composantes est de 1 pour 1 milliard à peu près. Il y a presque autant de neutrinos, d'antineutrinos, d'électrons et de positrons. Des réactions incessantes se produisent, changeant protons en neutrons et vice-versa. Cependant, l'égalité du nombre des leptons assure l'égalité entre la proportion de neutrons et de protons.
Après 0,11 s, la température descend à 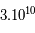 K, rien ne change de nature mais il est maintenant plus facile aux neutrons, plus lourds, de se transformer en protons. Les proportions ne sont plus symétriques : 38% de neutrons contre 62% de protons.
K, rien ne change de nature mais il est maintenant plus facile aux neutrons, plus lourds, de se transformer en protons. Les proportions ne sont plus symétriques : 38% de neutrons contre 62% de protons.
Après 1,09 s, à une température de 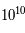 K, les neutrinos et antineutrinos qui interagissent bien moins fortement avec les autres particules deviennent libres. Ils peuvent alors se déplacer sans interagir avec la matière environnante. C'est le premier découplage. Ainsi, les neutrinos ont dû garder l'empreinte des conditions de l'univers à ses tous premiers instants de même que le FDC le fera plus tard. C'est donc une nouvelle voie pour étudier directement l'univers à des âges très reculés. La difficulté provient évidemment de la très faible interaction neutrino-matière qui rend quasiment impossible une observation fiable à l'heure actuelle. Le découplage interdit aux neutrons de se transformer en protons. Étant instables dans le vide, les neutrons sont alors voués à disparaître. Leur nombre continue de décroître : 76% de protons contre 24% de neutrons.
K, les neutrinos et antineutrinos qui interagissent bien moins fortement avec les autres particules deviennent libres. Ils peuvent alors se déplacer sans interagir avec la matière environnante. C'est le premier découplage. Ainsi, les neutrinos ont dû garder l'empreinte des conditions de l'univers à ses tous premiers instants de même que le FDC le fera plus tard. C'est donc une nouvelle voie pour étudier directement l'univers à des âges très reculés. La difficulté provient évidemment de la très faible interaction neutrino-matière qui rend quasiment impossible une observation fiable à l'heure actuelle. Le découplage interdit aux neutrons de se transformer en protons. Étant instables dans le vide, les neutrons sont alors voués à disparaître. Leur nombre continue de décroître : 76% de protons contre 24% de neutrons.
L'ère radiative
13,82 s après la fin de l'ère hadronique, la température est descendue jusqu'à 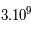 K. Les électrons et positrons se sont annihilés en photons et il reste seulement 1 électron sur 1 milliard, rejoignant le nombre de protons. Les photons sont maintenant majoritaires en densité d'énergie. L'ère leptonique est terminée et l'ère radiative a pris place. Les nucléons commencent à s'associer en deutérium, tritium et Hélium 3. Cependant, ces nouveaux noyaux atomiques ne sont pas assez stables à ces températures pour former un atome d'hélium qui, lui, aurait pu l'être. La proportion de neutrons continue de chuter : 17% de neutrons et 83% de protons.
K. Les électrons et positrons se sont annihilés en photons et il reste seulement 1 électron sur 1 milliard, rejoignant le nombre de protons. Les photons sont maintenant majoritaires en densité d'énergie. L'ère leptonique est terminée et l'ère radiative a pris place. Les nucléons commencent à s'associer en deutérium, tritium et Hélium 3. Cependant, ces nouveaux noyaux atomiques ne sont pas assez stables à ces températures pour former un atome d'hélium qui, lui, aurait pu l'être. La proportion de neutrons continue de chuter : 17% de neutrons et 83% de protons.
Après trois minutes, la température est de 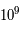 K, le nombre de neutrons a encore chuté à 14 %. Si le tritium et l'hélium 3 sont stable, le deutérium est quant à lui encore trop instable pour former des atomes plus complexes.
K, le nombre de neutrons a encore chuté à 14 %. Si le tritium et l'hélium 3 sont stable, le deutérium est quant à lui encore trop instable pour former des atomes plus complexes.
Passé le cap de l'instabilité du deutérium, à 3 min 46s, à 900 millions de Kelvins, la nucléosynthèse primordiale peut se mettre en marche. Il se forme des noyaux d'hélium avec les neutrons disponibles qui représentent maintenant 13% du nombre total des atomes. La température est trop élevée pour la formation de noyaux plus lourds que l'hélium en grand nombre. Il en résulte des fractions de masse de 25% d'hélium et de 75% de protons. C'est la nucléosynthèse primordiale.
L'expansion de l'univers fait décroître la densité d'énergie de la matière en diluant la masse. La densité d'énergie de la matière évolue en 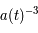 , où
, où 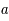 est le facteur d'expansion de l'univers vu au chapitre sur la relativité générale. De même, les photons sont dilués et leur longueur d'onde est dilatée par l'effet Doppler cosmologique. Leur densité d'énergie décroît donc plus vite, en
est le facteur d'expansion de l'univers vu au chapitre sur la relativité générale. De même, les photons sont dilués et leur longueur d'onde est dilatée par l'effet Doppler cosmologique. Leur densité d'énergie décroît donc plus vite, en 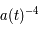 . L'équilibre entre l'énergie radiative et l'énergie de la matière se situe 60 000 ans après le Big Bang à
. L'équilibre entre l'énergie radiative et l'énergie de la matière se situe 60 000 ans après le Big Bang à 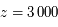 à une température de plus de 8 000 K. Suit alors l'ère stellaire où la matière domine le contenu énergétique.
à une température de plus de 8 000 K. Suit alors l'ère stellaire où la matière domine le contenu énergétique.
L'ère stellaire
L'ère stellaire connaît vraiment ses débuts lorsque, vers 380 000 ans après le début du Big Bang, la température a chuté vers 3 000 K. A ce moment, les électrons peuvent se stabiliser autour des noyaux atomiques et la lumière se découple de la matière. La lumière de cette époque deviendra après 13,7 milliards d'années le Fond Diffus Cosmologique étudié au chapitre précédent.
Passée l'époque de la recombinaison, l'univers est composé de trois systèmes indépendants : le système neutrino-antineutrino, le système de photons du FDC et la masse composée d'hydrogène et d'hélium. Chacun de ces systèmes évolue de manière quasi-indépendante. Les deux premiers ne feront que se refroidir tandis que la matière connaîtra une évolution plus complexe. La distribution de la matière va devenir de plus en plus inhomogène. Cette structuration de l'univers est l'objet du prochain chapitre.
Résumé
Pour ce chapitre qui résume l'histoire de l'univers des premiers instants jusqu'à aujourd'hui, un schéma est présenté pour résumer les différentes étapes, et pour donner les ordres de grandeurs associés à ces dernières.
Les ères cosmologiques
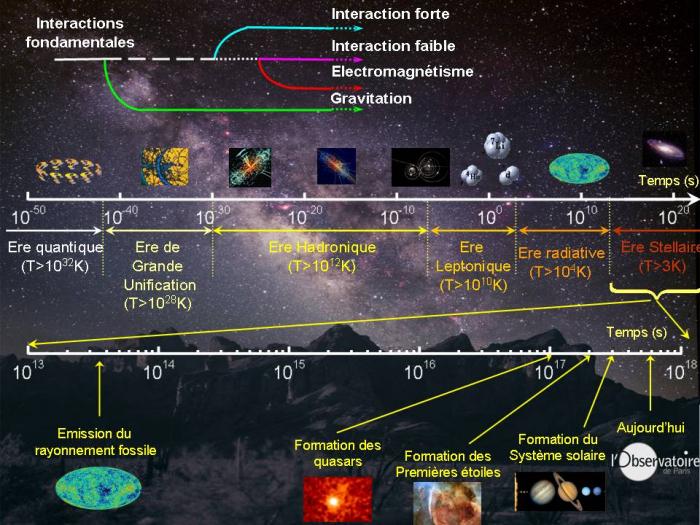
Ligne du temps et histoire thermique de l'Univers. On remarquera les échelles de temps très différentes entre les ères : l'ère stellaire dure à elle seule plus de 10 milliards d'années tandis que les ères précédentes durent de quelques infinitésimales fractions de seconde à quelques milliers d'années.
Crédit :
A. Füzfa
Réponses aux exercices
pages_univ-debut/exo-suba.html
Exercice
'Grandeurs caractéristiques'

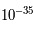 secondes).
secondes).
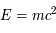 . La conversion de la masse en énergie qui en découle donne des Joules, l'unité standard. Puis, cette énergie est convertie en eV (électron-Volt, énergie que gagne un électron dans un champs de 1 Volt en une seconde) par la relation suivante : 1 eV =
. La conversion de la masse en énergie qui en découle donne des Joules, l'unité standard. Puis, cette énergie est convertie en eV (électron-Volt, énergie que gagne un électron dans un champs de 1 Volt en une seconde) par la relation suivante : 1 eV = 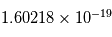 J. Par exemple, un proton ayant une masse de
J. Par exemple, un proton ayant une masse de 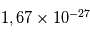 kg a une énergie de
kg a une énergie de 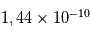 J qui équivaut à 900 MeV (Mega-eV).
J qui équivaut à 900 MeV (Mega-eV).
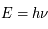 , où
, où 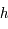 est la constante de Planck
est la constante de Planck 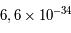 J.s et
J.s et 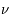 la fréquence du photon mais aussi l'énergie statistique moyenne des photons qui découle de la loi de Wien. Pour une température donnée, l'énergie des photons se situe au alentour du pic du corps noir. En moyenne, un photon, dans un corps noir d'une température de
la fréquence du photon mais aussi l'énergie statistique moyenne des photons qui découle de la loi de Wien. Pour une température donnée, l'énergie des photons se situe au alentour du pic du corps noir. En moyenne, un photon, dans un corps noir d'une température de 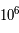 K, aura, d'après la loi de Wien, une longueur d'onde de 2,9 nm ce qui correspond à une énergie de
K, aura, d'après la loi de Wien, une longueur d'onde de 2,9 nm ce qui correspond à une énergie de 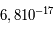 J ou 426 eV.
J ou 426 eV.
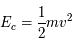 où
où 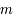 est sa masse et
est sa masse et 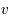 sa vitesse. On peut aussi dans le cas d'un corps noir parler d'énergie statistique des particules reliant leurs vitesses et la température du corps noir :
sa vitesse. On peut aussi dans le cas d'un corps noir parler d'énergie statistique des particules reliant leurs vitesses et la température du corps noir : 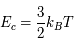 où
où 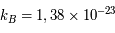 m2.kg.s-2.K-1 est la constante de Boltzmann et
m2.kg.s-2.K-1 est la constante de Boltzmann et 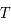 la température du corps noir. En moyenne, un proton dans un plasma de corps noir à la température de
la température du corps noir. En moyenne, un proton dans un plasma de corps noir à la température de 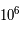 K aura une énergie cinétique égale à
K aura une énergie cinétique égale à 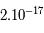 J = 129 eV qui correspond à une vitesse de 160 km/s.
J = 129 eV qui correspond à une vitesse de 160 km/s.


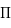 ,
, 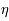 , ...), ou celle des hypérons (
, ...), ou celle des hypérons (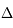 ,
, 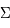 , ...). Le schéma ci-joint résume clairement ces différentes familles. Les hadrons forment une structure complexe car ce ne sont pas des particules élémentaires. Elles sont elle-mêmes l'association de particules élémentaires, les quarks, jusqu'à preuve du contraire. Par exemple, le proton est l'assemblage de trois quarks : deux quarks up et un quark down. A l'inverse, le neutron est constitué de deux quarks down et d'un quark up. Les hadrons ont une masse, une charge et un spin. Ils peuvent donc ressentir les interactions gravitationnelles et électromagnétiques sauf si leur charge est nulle comme pour le neutron. En plus de cela, ils sont sujets par définition à l'interaction forte et faible. A chaque hadron est associé un nombre hadronique. Par exemple, le neutron et le proton ont un nombre hadronique de 1. Ce nombre doit être conservé dans une transformation tout comme est conservée la charge électrique.
, ...). Le schéma ci-joint résume clairement ces différentes familles. Les hadrons forment une structure complexe car ce ne sont pas des particules élémentaires. Elles sont elle-mêmes l'association de particules élémentaires, les quarks, jusqu'à preuve du contraire. Par exemple, le proton est l'assemblage de trois quarks : deux quarks up et un quark down. A l'inverse, le neutron est constitué de deux quarks down et d'un quark up. Les hadrons ont une masse, une charge et un spin. Ils peuvent donc ressentir les interactions gravitationnelles et électromagnétiques sauf si leur charge est nulle comme pour le neutron. En plus de cela, ils sont sujets par définition à l'interaction forte et faible. A chaque hadron est associé un nombre hadronique. Par exemple, le neutron et le proton ont un nombre hadronique de 1. Ce nombre doit être conservé dans une transformation tout comme est conservée la charge électrique.
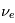 , ont un nombre leptonique de 1.
, ont un nombre leptonique de 1.
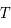 , la vitesse moyenne d'une particule vaut :
, la vitesse moyenne d'une particule vaut :
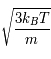
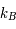 est la constante de Boltzmann,
est la constante de Boltzmann, 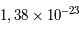 m2.kg.s-2.K-1,
m2.kg.s-2.K-1, 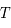 la température en Kelvin et m la masse en kg. Quelle est la vitesse d'un proton à 3 000 K et à 3x109 K ? Vérifier que nous sommes bien dans un régime classique et non relativiste.
la température en Kelvin et m la masse en kg. Quelle est la vitesse d'un proton à 3 000 K et à 3x109 K ? Vérifier que nous sommes bien dans un régime classique et non relativiste.
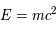 où c est la vitesse de la lumière, celui d'un photon est
où c est la vitesse de la lumière, celui d'un photon est 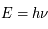 avec
avec 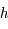 la constante de Planck et
la constante de Planck et 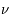 a fréquence du photon.
a fréquence du photon.
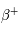 qui transforme un proton en neutron et libère un positron. Cette désintégration intervient au sein des noyaux atomiques dans la matière dite radioactive comme l'Uranium 235. Les rayons cosmiques peuvent aussi générer des anti-particules. En effet, ces derniers sont des particules provenant de l'espace et ayant une grande énergie cinétique, donc une vitesse proche de celle de la lumière. Ce sont souvent des protons. En pénétrant dans l'atmosphère, ils rentrent en collision avec des particules de gaz et forment une gerbe de particules contenant des anti-particules. Historiquement, le positron fut découvert à la suite d'un rayon cosmique. Les accélérateurs de particules sont un autre moyen de créer des anti-particules. Le principe est le même que pour les rayons cosmiques sauf que c'est un accélérateur de particules créé par l'homme qui accélère un proton grâce à de puissants champs magnétiques et le fait collisionner dans une immense chambre pour étudier avec précision les particules résultantes de la collision. Néanmoins, exceptés ces trois processus, l'univers semble dépourvu d'antimatière. En effet, au contact de la matière, l'antimatière s'annihile pour former des photons très énergétiques. Si une partie de notre univers était faite d'antimatière nous devrions voir la limite avec la zone de matière par un dégagement de lumière intense, or il n'en est rien. On peut toujours rêver à une zone de l'univers si bien isolée et éloignée de nous que l'antimatière aurait survécu, mais cela est de plus en plus improbable.
qui transforme un proton en neutron et libère un positron. Cette désintégration intervient au sein des noyaux atomiques dans la matière dite radioactive comme l'Uranium 235. Les rayons cosmiques peuvent aussi générer des anti-particules. En effet, ces derniers sont des particules provenant de l'espace et ayant une grande énergie cinétique, donc une vitesse proche de celle de la lumière. Ce sont souvent des protons. En pénétrant dans l'atmosphère, ils rentrent en collision avec des particules de gaz et forment une gerbe de particules contenant des anti-particules. Historiquement, le positron fut découvert à la suite d'un rayon cosmique. Les accélérateurs de particules sont un autre moyen de créer des anti-particules. Le principe est le même que pour les rayons cosmiques sauf que c'est un accélérateur de particules créé par l'homme qui accélère un proton grâce à de puissants champs magnétiques et le fait collisionner dans une immense chambre pour étudier avec précision les particules résultantes de la collision. Néanmoins, exceptés ces trois processus, l'univers semble dépourvu d'antimatière. En effet, au contact de la matière, l'antimatière s'annihile pour former des photons très énergétiques. Si une partie de notre univers était faite d'antimatière nous devrions voir la limite avec la zone de matière par un dégagement de lumière intense, or il n'en est rien. On peut toujours rêver à une zone de l'univers si bien isolée et éloignée de nous que l'antimatière aurait survécu, mais cela est de plus en plus improbable.

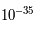 seconde après le Big Bang, l'Univers contenait des nombres de particules (représentées par des points jaunes) et d'antiparticules (en bleu) proches, mais avec un nombre très légèrement plus grand de particules. Cette animation montre le processus d'annihilation des particules et d'antiparticules. Cependant, il subsiste le léger déséquilibre entre particules et antiparticules.
seconde après le Big Bang, l'Univers contenait des nombres de particules (représentées par des points jaunes) et d'antiparticules (en bleu) proches, mais avec un nombre très légèrement plus grand de particules. Cette animation montre le processus d'annihilation des particules et d'antiparticules. Cependant, il subsiste le léger déséquilibre entre particules et antiparticules.
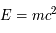 , où
, où 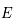 est l'énergie de masse d'une particule,
est l'énergie de masse d'une particule, 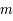 sa masse et
sa masse et 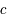 la vitesse de la lumière. Cette relation nous dévoile le fait qu'il existe une équivalence entre matière et énergie. Il est alors possible de transformer l'une en l'autre. Cependant, comme dans une réaction nucléaire, la charge, le nombres baryonique et leptonique doivent être conservés, donc cela interdit certaines réactions. Par exemple, la réaction suivante :
la vitesse de la lumière. Cette relation nous dévoile le fait qu'il existe une équivalence entre matière et énergie. Il est alors possible de transformer l'une en l'autre. Cependant, comme dans une réaction nucléaire, la charge, le nombres baryonique et leptonique doivent être conservés, donc cela interdit certaines réactions. Par exemple, la réaction suivante :
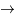 neutron + électron
neutron + électron
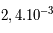 nm, soit des rayons gamma. Le rayonnement visible (400-800 nm) est bien trop faible énergétiquement pour créer des particules élémentaires.
nm, soit des rayons gamma. Le rayonnement visible (400-800 nm) est bien trop faible énergétiquement pour créer des particules élémentaires.
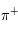 est constitué d'un quark
est constitué d'un quark 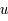 et d'un antiquark
et d'un antiquark 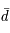 . Quelle est sa charge ? Quelle est son antiparticule et la charge de celle-ci ?
. Quelle est sa charge ? Quelle est son antiparticule et la charge de celle-ci ?
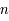
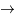
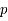 +
+ 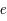 +
+ 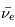
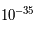 premières secondes, sont terra incognita.
premières secondes, sont terra incognita.
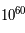 faisant passer des inhomogénéités sur des échelles microscopiques à des échelles macroscopiques. C'est aussi à la fin de cette époque que les quarks se seraient assemblés pour former les hadrons : muons, protons, neutrons, ...
faisant passer des inhomogénéités sur des échelles microscopiques à des échelles macroscopiques. C'est aussi à la fin de cette époque que les quarks se seraient assemblés pour former les hadrons : muons, protons, neutrons, ...
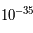 premières secondes. Le Large Hadron Collider (LHC large collisionneur d'hadron) devrait donner des pistes en produisant des énergies de l'ordre du Tev (
premières secondes. Le Large Hadron Collider (LHC large collisionneur d'hadron) devrait donner des pistes en produisant des énergies de l'ordre du Tev (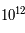 eV) ce qui correspond à une température de l'ordre de
eV) ce qui correspond à une température de l'ordre de 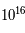 K.
K.
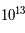 K jusqu'à une température de
K jusqu'à une température de 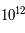 K, lorsque la température seuil du plus léger des hadrons est atteinte : le méson
K, lorsque la température seuil du plus léger des hadrons est atteinte : le méson 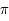 neutre (
neutre ( 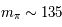 Mev/
Mev/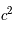 ). Cette ère dure seulement un dix-millioniène de seconde. Les hadrons et leurs antiparticules forment alors un système en équilibre thermodynamique. Leurs masses imposantes face aux leptons en font la composante dominante de la matière de cette époque. L'origine de la prédominance de la matière sur l'antimatière dans l'univers contemporain est à situer au coeur de ces ères, comme une conséquence possible de l'asymétrie de leurs propriétés dans les processus de création-annihilation qui régissaient l'équilibre thermodynamique. Cependant, cela reste encore une question très débattue.
). Cette ère dure seulement un dix-millioniène de seconde. Les hadrons et leurs antiparticules forment alors un système en équilibre thermodynamique. Leurs masses imposantes face aux leptons en font la composante dominante de la matière de cette époque. L'origine de la prédominance de la matière sur l'antimatière dans l'univers contemporain est à situer au coeur de ces ères, comme une conséquence possible de l'asymétrie de leurs propriétés dans les processus de création-annihilation qui régissaient l'équilibre thermodynamique. Cependant, cela reste encore une question très débattue.
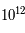 K et
K et 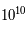 K, pendant un peu plus d'une seconde, l'univers se situe dans l'ère leptonique. La température de seuil des hadrons n'est plus atteinte. Les hadrons et leurs anti-particules se sont annihilés pour la plupart. Du fait d'une très légère dissymétrie avant l'annihilation, quelques hadrons ont survécu, un sur un milliard en ordre de grandeur. Il ne reste alors que des protons et des neutrons. L'univers est rempli de photons, de neutrinos, d'anti-neutrinos, d'électrons et de positrons. Le rapport entre les hadrons et les autres composantes est de 1 pour 1 milliard à peu près. Il y a presque autant de neutrinos, d'antineutrinos, d'électrons et de positrons. Des réactions incessantes se produisent, changeant protons en neutrons et vice-versa. Cependant, l'égalité du nombre des leptons assure l'égalité entre la proportion de neutrons et de protons.
K, pendant un peu plus d'une seconde, l'univers se situe dans l'ère leptonique. La température de seuil des hadrons n'est plus atteinte. Les hadrons et leurs anti-particules se sont annihilés pour la plupart. Du fait d'une très légère dissymétrie avant l'annihilation, quelques hadrons ont survécu, un sur un milliard en ordre de grandeur. Il ne reste alors que des protons et des neutrons. L'univers est rempli de photons, de neutrinos, d'anti-neutrinos, d'électrons et de positrons. Le rapport entre les hadrons et les autres composantes est de 1 pour 1 milliard à peu près. Il y a presque autant de neutrinos, d'antineutrinos, d'électrons et de positrons. Des réactions incessantes se produisent, changeant protons en neutrons et vice-versa. Cependant, l'égalité du nombre des leptons assure l'égalité entre la proportion de neutrons et de protons.
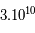 K, rien ne change de nature mais il est maintenant plus facile aux neutrons, plus lourds, de se transformer en protons. Les proportions ne sont plus symétriques : 38% de neutrons contre 62% de protons.
K, rien ne change de nature mais il est maintenant plus facile aux neutrons, plus lourds, de se transformer en protons. Les proportions ne sont plus symétriques : 38% de neutrons contre 62% de protons.
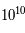 K, les neutrinos et antineutrinos qui interagissent bien moins fortement avec les autres particules deviennent libres. Ils peuvent alors se déplacer sans interagir avec la matière environnante. C'est le premier découplage. Ainsi, les neutrinos ont dû garder l'empreinte des conditions de l'univers à ses tous premiers instants de même que le FDC le fera plus tard. C'est donc une nouvelle voie pour étudier directement l'univers à des âges très reculés. La difficulté provient évidemment de la très faible interaction neutrino-matière qui rend quasiment impossible une observation fiable à l'heure actuelle. Le découplage interdit aux neutrons de se transformer en protons. Étant instables dans le vide, les neutrons sont alors voués à disparaître. Leur nombre continue de décroître : 76% de protons contre 24% de neutrons.
K, les neutrinos et antineutrinos qui interagissent bien moins fortement avec les autres particules deviennent libres. Ils peuvent alors se déplacer sans interagir avec la matière environnante. C'est le premier découplage. Ainsi, les neutrinos ont dû garder l'empreinte des conditions de l'univers à ses tous premiers instants de même que le FDC le fera plus tard. C'est donc une nouvelle voie pour étudier directement l'univers à des âges très reculés. La difficulté provient évidemment de la très faible interaction neutrino-matière qui rend quasiment impossible une observation fiable à l'heure actuelle. Le découplage interdit aux neutrons de se transformer en protons. Étant instables dans le vide, les neutrons sont alors voués à disparaître. Leur nombre continue de décroître : 76% de protons contre 24% de neutrons.
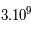 K. Les électrons et positrons se sont annihilés en photons et il reste seulement 1 électron sur 1 milliard, rejoignant le nombre de protons. Les photons sont maintenant majoritaires en densité d'énergie. L'ère leptonique est terminée et l'ère radiative a pris place. Les nucléons commencent à s'associer en deutérium, tritium et Hélium 3. Cependant, ces nouveaux noyaux atomiques ne sont pas assez stables à ces températures pour former un atome d'hélium qui, lui, aurait pu l'être. La proportion de neutrons continue de chuter : 17% de neutrons et 83% de protons.
K. Les électrons et positrons se sont annihilés en photons et il reste seulement 1 électron sur 1 milliard, rejoignant le nombre de protons. Les photons sont maintenant majoritaires en densité d'énergie. L'ère leptonique est terminée et l'ère radiative a pris place. Les nucléons commencent à s'associer en deutérium, tritium et Hélium 3. Cependant, ces nouveaux noyaux atomiques ne sont pas assez stables à ces températures pour former un atome d'hélium qui, lui, aurait pu l'être. La proportion de neutrons continue de chuter : 17% de neutrons et 83% de protons.
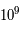 K, le nombre de neutrons a encore chuté à 14 %. Si le tritium et l'hélium 3 sont stable, le deutérium est quant à lui encore trop instable pour former des atomes plus complexes.
K, le nombre de neutrons a encore chuté à 14 %. Si le tritium et l'hélium 3 sont stable, le deutérium est quant à lui encore trop instable pour former des atomes plus complexes.
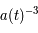 , où
, où 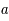 est le facteur d'expansion de l'univers vu au chapitre sur
est le facteur d'expansion de l'univers vu au chapitre sur 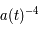 . L'équilibre entre l'énergie radiative et l'énergie de la matière se situe 60 000 ans après le Big Bang à
. L'équilibre entre l'énergie radiative et l'énergie de la matière se situe 60 000 ans après le Big Bang à 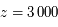 à une température de plus de 8 000 K. Suit alors l'ère stellaire où la matière domine le contenu énergétique.
à une température de plus de 8 000 K. Suit alors l'ère stellaire où la matière domine le contenu énergétique.
