 Introduction
Introduction
Nous étudions maintenant les éclipses de Soleil sur de très grandes période de temps, pour cela nous construisons des canons d'éclipses.
Les parties pour en savoir plus vous donnent les caractéristiques du canon d'éclipses construit à l'IMCCE, ainsi que les listes des éclipses totales et annulaires les plus longues et des éclipses partielles les plus courtes avec des détails et des commentaires.
Les listes d'éclipses de Lune et de Soleil sont publiées dans des livres appelés canons d'éclipses. Le plus connu est celui de Theodor Ritter von Oppolzer, sa première édition date de 1887 dans le volume 52 des Mémoires de Mathématiques et de Sciences Naturelles de l'Académie Impériale de Vienne. Ce canon, corrigé, est réédité régulièrement. Dans ce canon, on trouve 8000 éclipses de Soleil comprises entre -1207 et 2161 et 5200 éclipses de Lune comprises entre -1206 et 2132. Il faut préciser que l'on n'y trouve pas les éclipses de Lune par la pénombre.
Il convient de citer également le canon des éclipses de Soleil de Jean Meeus et Hermann Mucke (1983, Astronomisches Büro, Vienne), contenant toutes les éclipses de Soleil comprises entre -2003 et 2526.
À l'IMCCE, nous avons construit un canon d'éclipses de Lune et de Soleil. Il porte sur une période de 6000 ans (de l'an -2999 à 3000), il a été construit avec les dernières théories planétaires et lunaire élaborées à l'IMCCE.
Ces trois canons ont été construits avec des théories différentes des corps célestes et avec des constantes légèrement différentes, cela implique que certaines éclipses limites ne sont pas identiques (apparition de nouvelles éclipses limites, ou éclipses totales dans un canon qui deviennent mixtes dans l'autre).
 En savoir plus
En savoir plus
Pour construire notre canon nous avons utilisé les théories suivantes :
- Théorie de la Lune : ELP2000 de Michèle Chapront-Touzé et J. Chapront.
- Théorie du barycentre Terre-Lune : VSOP82 de P. Bretagnon.
- Éphémérides sous forme de polynômes de Tchebycheff : SLP98 de G. Francou
- TT-TU : valeurs de R. Stephenson (1984) modifiées et adaptées à la théorie de la Lune utilisée.
- Théorie de la précession de Lieske (1977).
- Théorie de la nutation de Wahr (1981).
- Temps sidéral d'Aoki (1992)
 En savoir plus
En savoir plus
Les paramètres physiques utilisés sont les suivants :
- le demi-diamètre solaire = 15' 59.63"
- le rapport du rayon lunaire sur le rayon équatorial terrestre : k = 0,2725076
- le rayon équatorial terrestre = 6 378 140 m
- le carré de l'ellipticité de l'ellipsoïde terrestre = 0,00669438 -- 1/f = 1/298.257 IERS (1992)
 En savoir plus
En savoir plus
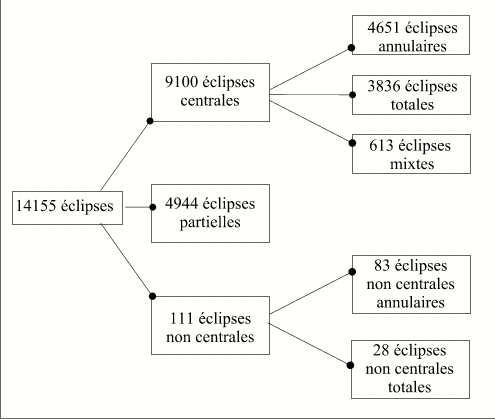
Nous avons trouvé sur cette période de 6000 ans, 14 155 éclipses de Soleil qui se répartissent de la manière suivante :
Crédit : IMCCE/Patrick Rocher
Comme on l'a prédit précédemment, on constate qu'il y a bien plus d'éclipses annulaires que d'éclipses totales.
Une éclipse totale a une durée maximale lorsque l'ombre est la plus grande possible, c'est-à-dire lorsque la Terre est à l'aphélie pour avoir le plus petit diamètre apparent du Soleil, lorsque la Lune est au périgée pour avoir le plus gros diamètre apparent de la Lune et lorsque le maximum a lieu au zénith du lieu d'observation pour avoir une distance observateur Lune minimale, donc un diamètre de l'ombre maximal. La première condition fixe la date de l'éclipse (actuellement début juillet). La troisième condition fixe le lieu d'observation proche du tropique du Cancer (latitude 23°). Avec la Lune au périgée, la vitesse synodique de l'ombre par rapport à la Terre est de 3 733 km/h (1 037 m/s) et la vitesse de l'ombre sur la surface de la Terre est de 2 196 km/h (610 m/s), le diamètre de l'ombre est alors de 262 km et la durée de l'éclipse est de 7 min 10 s. En réalité, ces paramètres ne sont pas indépendants et l'on s'aperçoit, en faisant un calcul plus rigoureux, que si l'on descend en latitude vers +5° la durée de l'éclipse croît jusqu'à environ 7 min 30 s. En effet le diamètre de l'ombre va décroître (on n'est plus au zénith, l'ombre devient ovale) mais sa vitesse décroît encore plus rapidement ce qui en fin de compte augmente sensiblement la durée de l'éclipse. Le tableau suivant porte sur l'ensemble des éclipses totales comprises entre l'an -2999 et 3000 issues du canon d'éclipses de Soleil de l'IMCCE.
| Date |
Durée |
Date |
Durée |
Date |
Durée |
| 29 mai -2584 |
7 min 17,00 s |
10 juin - 2566 |
7 min 23,76 s |
20 juin - 2548 |
7 min 19,94 s |
| 25 avril - 2266 |
7 min 10,49 s |
05 avril - 2248 |
7 min 23,37 s |
16 avril - 2230 |
7 min 27,25 s |
| 27 mai -2212 |
7 min 21,11 s |
8 juin - 1106 |
7 min 10,61 s |
24 mai - 779 |
7 min 13,45 s |
| 05 juin - 761 |
7 min 28,61 s |
15 juin - 743 |
7 min 31,73 s |
26 juin -725 |
7 min 23,45 s |
| 11 mai - 425 |
7 min 16,51 s |
22 mai - 407 |
7 min 18,11 s |
02 juin - 389 |
7 min 10,01 s |
| 22 mai 114 |
7 min 10,41 s |
01 juin 132 |
7 min 19,50 s |
12 juin 150 |
7 min 17,99 s |
| 16 juin 345 |
7 min 21,13 s |
27 juin 363 |
7 min 28,42 s |
08 juillet 381 |
7 min 26,87 s |
| 19 juillet 399 |
7 min 15,75 s |
23 mai 681 |
7 min 14,32 s |
03 juin 699 |
7 min 21,62 s |
| 13 juin 717 |
7 min 20,47 s |
29 mai 1044 |
7 min 16,79 s |
09 juillet 1062 |
7 min 25,27 s |
| 20 juin 1080 |
7 min 22,83 s |
01 juillet 1098 |
7 min 10,21 s |
20 juin 1955 |
7 min 12,62 s |
| 25 juin 2150 |
7 min 18,77 s |
05 juillet 2168 |
7 min 30,89 s |
16 juillet 2186 |
7 min 34,14 s |
| 27 juillet 2204 |
7 min 26,93 s |
08 août 2222 |
7 min 10,39 s |
14 juin 2504 |
7 min 15,03s |
| 25 juin 2522 |
7 min 17,54 s |
23 juin 2867 |
7 min 14,67 s |
03 juillet 2885 |
7 min 15,80 s |
Liste des éclipses totales d'une durée supérieure à 7 minutes et 10 secondes
On constate que l'éclipse la plus longue sera celle du 16 juillet 2186 pour une durée de 7 min 34,14 s, valeur légèrement supérieure à celle calculée avec les valeurs moyennes.
Dans le cas d'une éclipse annulaire le raisonnement est similaire aux éclipses totales, mais inverse. Le diamètre apparent du Soleil doit être le plus grand possible donc la Terre doit être au périhélie et le diamètre apparent de la Lune doit être le plus petit possible donc la Lune doit être à l'apogée, dans ce cas la durée maximale de l'éclipse peut atteindre 12 min 30 s. Le tableau suivant porte sur l'ensemble des éclipses annulaires comprises entre l'an -2999 et 3000 issues du canon d'éclipses de Soleil de l'IMCCE .
| Date |
Durée |
Date |
Durée
|
| 12 décembre -1655 |
11 min 53,93 s |
10 décembre - 195 |
11 min 57,93 s |
| 22 décembre - 177 |
12 min 01,43 s |
25 novembre 132 |
12 min 08.01 s |
| 06 décembre 150 |
12 min 15,91 s |
17 décembre 168 |
12 min 07.25 s |
| 25 décembre 1628 |
11 min 55,47 s |
02 décembre 1937 |
11 min 53.63 s |
| 14 décembre 1955 |
12 min 02,49 s |
24 décembre 1973 |
11 min 55.75 s |
Liste des éclipses annulaires d'une durée supérieure à 11 minutes et 50 secondes
À l'aide du canon d'éclipses de Soleil de l'IMCCE nous avons cherché quelles sont les éclipses partielles les plus petites sur la période -2999, 3000. Nous avons trouvé les deux éclipses suivantes :
| Date |
Magnitude |
Instant du maximum |
Durée générale |
| 23 juillet 651 |
0,0008272 |
08h 30 m 41,06 s UT |
9,3 min |
| 17 août 1327 |
0,0004937 |
16 h 58 m 33,03 s UT |
6,2 min |
Nous allons étudier ces deux éclipses.
Éphémérides de la Lune au voisinage de l'éclipse :
- le 15/07/0651 à 07h 31m 28s UT : Dernier Quartier.
- le 22/07/0651 à 01h 25m 11s UT : la Lune passe par le noeud descendant de son orbite.
- le 22/07/0651 à 14h 50m 11s UT : la Lune à l'apogée, d=406450 km, diam. app. =29,5'.
- le 23/07/0651 à 08h 30m 41s UT : maximum de l'éclipse.
- le 23/07/0651 à 08h 47m 30s UT : Nouvelle Lune.
On constate que cette éclipse a lieu après le passage au noeud descendant de l'orbite lunaire, comme l'éclipse est très faible le passage au noeud doit être loin de la conjonction et l'instant du maximum de l'éclipse loin de l'instant de la conjonction. C'est effectivement le cas, on a un écart de temps égal à 16m 49s entre la conjonction et le maximum de l'éclipse et on a également un écart de temps maximal égal à 31h 22m 19s entre la conjonction et le passage au noeud. Ces valeurs sont presque des valeurs extrêmes car la Lune est voisine de son apogée et la Terre est proche de son aphélie, donc la Lune et le Soleil se déplacent lentement. On remarque que comme nous l'avons expliqué précédemment le maximum de l'éclipse (distance minimale entre le centre de la Lune et le centre du Soleil) a bien lieu entre le passage au noeud et la conjonction.
Éphémérides de la Lune au voisinage de l'éclipse :
- le 14/08/1327 à 15h 01m 55s UT : la Lune au périgée d=365783 km, diam. app. =32,7'.
- le 17/08/1327 à 16h 43m 04s UT : Nouvelle Lune.
- le 17/08/1327 à 16h 58m 33s UT : maximum de l'éclipse.
- le 18/08/1327 à 21h 34m 46s UT : la Lune passe par le noeud ascendant de son orbite.
- le 25/08/1327 à 06h 20m 50s UT : Premier Quartier.
- le 26/08/1327 à 12h 15m 12s UT : la Lune à l'apogée d=404381 km, diam. app. =29,6'.
Cette éclipse a lieu avant le passage au noeud ascendant, on a donc le scénario suivant, conjonction, maximum de l'éclipse et passage au noeud. L'écart de temps entre la conjonction et le maximum de l'éclipse est de 15m 29s et l'écart de temps entre la conjonction et le passage au noeud est de 28h 36m 13s.
Pour ces deux éclipses, qui sont des cas extrêmes, on voit que le maximum de l'éclipse est relativement proche de la conjonction, par contre la conjonction est très éloignée du passage au noeud (plus d'une journée).
 Introduction
Introduction