

Cycles astronomiques et fractions continues |
Auteur: Alexandre Pousse
Les fractions continues ont une très longue histoire car liées à celle des nombres. En effet, il existe un lien important entre celles-ci et l'algorithme d'Euclide. Plus particulièrement, elles apparaissent dans l'approximation de nombre comme π ou du nombre d'or.
Délaissées pendant un certain temps, elles sont redécouvertes en Europe en 1655 par le mathématicien anglais John Wallis, puis étudiées par la suite par Leonhard Euler qui va apporter de nombreux théorèmes.
L'interêt de l'étude des fractions continues est souvent pour l'approximation d'équations diophantiennes. Ce sont des équations algébriques pour lesquelles on cherche des solutions en entiers. Un exemple particulier qui est utile en astronomie car permettant de mettre en évidence des phénomènes de résonnances ou de prévoir le retour d'un phénomène périodique, c'est de fixer 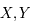 deux nombres représentant des périodes, et de trouver
deux nombres représentant des périodes, et de trouver 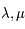 , deux entiers tels que
, deux entiers tels que 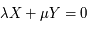 . La notion d'approximation introduite par les fractions continues est utilisée lorsque
. La notion d'approximation introduite par les fractions continues est utilisée lorsque 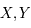 sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant
sont irrationnelles ou rationnelles comportant de nombreuses décimales (ce qui est fréquent de manière générale en Physique), on va alors chercher à trouver la meilleure combinaison linéaire approximant 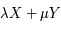 .
Autre application des fractions conitnues: en arithmétique, elles vont permettre l'étude et la caractérisation de nombres transcendants (par exemple, par l'étude de leur périodicité).
.
Autre application des fractions conitnues: en arithmétique, elles vont permettre l'étude et la caractérisation de nombres transcendants (par exemple, par l'étude de leur périodicité).
Une fraction continue est un objet s'écrivant sous la forme 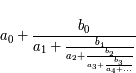 où les
où les 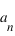 et les
et les 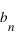 sont des nombres entiers naturels ou relatifs.
La fraction obtenue peut être composée d'un nombre fini ou infini de termes.
sont des nombres entiers naturels ou relatifs.
La fraction obtenue peut être composée d'un nombre fini ou infini de termes.
Mais ce que nous utiliserons par la suite et qui ont été étudiées plus particulièrement, ce sont les fractions continues simples, c'est-à-dire de la forme 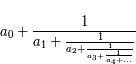 avec
avec 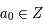 et
et 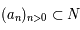 (fini ou non). Une notation plus compacte et qui sera utilisée ici est d'écrire
(fini ou non). Une notation plus compacte et qui sera utilisée ici est d'écrire ![[a_0;a_1;a_2;...;a_n;...]](../pages_quotient/equations_quotient/equation57.png) .
.
Afin de caractériser une fraction continue, on utilise la notion de réduite. Par exemple, pour 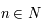 , on appellera réduite de la fraction continue définie par la suite
, on appellera réduite de la fraction continue définie par la suite 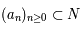 , la fraction
, la fraction ![\frac{p_n}{q_n}=[a_0;a_1;a_2;a_3;...;a_n]](../pages_quotient/equations_quotient/equation60.png) . Pour le nombre d'or
. Pour le nombre d'or 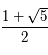 , les trois premières réduites sont
, les trois premières réduites sont ![\frac{p_0}{q_0}= [1]](../pages_quotient/equations_quotient/equation62.png) ,
, ![\frac{p_1}{q_1}=[1;1]](../pages_quotient/equations_quotient/equation63.png) ,
, ![\frac{p_2}{q_2}=[1;1;1]](../pages_quotient/equations_quotient/equation64.png) .
Ainsi, nous obtenons deux suites d'entiers
.
Ainsi, nous obtenons deux suites d'entiers 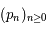 et
et 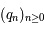 avec en particulier, la propriété suivante:
si
avec en particulier, la propriété suivante:
si 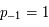 ,
, 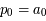 et
et 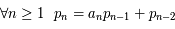 , et si
, et si 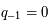 ,
, 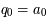 et
et 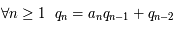 , alors
, alors ![\forall n \geq 0~~ \frac{p_n}{q_n} = [a_0;a_1;a_2;a_3;...a_n]](../pages_quotient/equations_quotient/equation73.png) .
.
Introduisons maintenant la fraction continue dans le cadre de l'approximation des nombres. Soit α un réel et 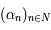 une suite de réels telle que:
une suite de réels telle que:
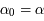 ,
,
si 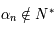 alors
alors 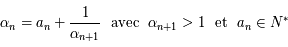 ,
,
sinon 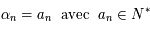 .
.
Ainsi, on obtient le développement suivant ![\alpha = a_0 + \frac{1}{\alpha_1}= a_0 + \frac{1}{a_1 + \frac{1}{\alpha_2}}} = a_0 + \frac{1}{a_1 + \frac{1}{a_2+ \frac{1}{\alpha_3}}}}=...=[a_0;a_1;a_2;...;a_n+ \frac{1}{\alpha_{n+1}}]=...](../pages_quotient/equations_quotient/equation79.png)
L'intérêt des fractions continues dans le domaine de l'astronomie est lié à la notion de périodicité ou de résonnance et donc aux équations diophantiennes qui en résultent. En effet, si l'on considère deux phénomènes ayant chacun une période 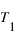 et
et 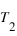 , alors afin de caractériser le retour mutuel de ces deux phénomènes, il est commode de chercher deux entiers X et Y tels que
, alors afin de caractériser le retour mutuel de ces deux phénomènes, il est commode de chercher deux entiers X et Y tels que 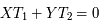 . Or généralement, les périodes ne sont malheureusement pas des nombres entiers ce qui implique de grands nombres entiers pour X et Y.
. Or généralement, les périodes ne sont malheureusement pas des nombres entiers ce qui implique de grands nombres entiers pour X et Y.
L'idée est donc de chercher les "meilleurs" rationnels 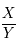 approchant
approchant 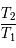 de façon à résoudre le problème au voisinage de la résonnance. C'est ce qu'on appelle l'approximation diophantienne. Nous utiliserons pour cela les fractions continues.
de façon à résoudre le problème au voisinage de la résonnance. C'est ce qu'on appelle l'approximation diophantienne. Nous utiliserons pour cela les fractions continues.
Les exercices qui suivent vont ainsi permettre de mettre en évidence la propriété théorique sur les réduites ainsi que des applications astronomique par la recherche de meilleure solution approximation de l'équation diophantienne via les fractions continues en caractérisant le mouvement de Saturne et de la Terre, le phénomène d'éclipse et en définissant une meilleure approximation de l'année tropique.