Qu'est-ce que cela veut dire ?
Faire des statistiques c'est :
- Dénombrer ou recenser : compter de manière exhaustive, sur toute la population répondant à un ou des critères bien définis
- Sonder : grâce aux techniques de la probabilité, c'est à dire qu'on n'étudie qu'un échantillon de la population et on en déduit des propriétés générales
Souvent les activités de recensement et de sondage coexistent. Elles ne sont pas différenciées dans l'énoncé des résultats. L'analyse des résultats, dernière étape de l'étude statistique est très souvent oubliée par les non spécialistes. Attention donc à ne pas réduire les statistiques aux sondages d'opinion !
L'opinion sur les statistiques est en général, pour les plus sceptiques, "on leur fait dire n'importe quoi
!" et, pour les plus crédules qui ont foi dans la "vérité" des chiffres "les chiffres ont parlé
!". Une attitude sage face à un résultat statistique est bien sûr "un esprit critique", ce qui exige un minimum de connaissances de base des statistiques.
Depuis les années 1980, l'Éducation Nationale a introduit dans le programme des collèges et lycées l'étude des statistiques et des probabilités. Un minimum de connaissance du vocabulaire, des méthodes et des techniques de la statistique est donc donné aux élèves.
Le mot "statistique" vient du latin "status" (état). Les statistiques sont utilisées depuis très longtemps. En Chine, des données de recensements ont été retrouvées datant du XXIIIe siècle av. JC, en Mésopotamie et en Égypte il y a 4500 ans. Les empereurs romains organisaient des enquêtes sur les richesses de leur empire, le nombre de soldats, leur armement … et tenaient des comptes.
Ce système de recueil de données se poursuit jusqu'au XVIIe siècle. En Europe, le rôle de collecteur de données a souvent été tenu par les guildes marchandes, puis par les intendants de l'État.
Les pays où existe un pouvoir fort, s'appuient sur des données de recensements pour confirmer leur pouvoir et favoriser leur rayonnement, mais rapidement l'augmentation de la taille des États, des populations a rendu le recensement long et coûteux. Ce même besoin existe de nos jours, les États, les banques, le monde des assurances s'appuient sur les statistiques pour la gestion, la compétition économique … à des fins décisionnelles.
Au XVIIe siècle, Pierre de Fermat et Blaise Pascal furent des précurseurs en calcul des probabilités. En cherchant à résoudre des problèmes posés par les jeux de hasard (jeux de dés, lancers de pièces), ils ont mis leurs compétences de mathématiciens au service du développement d'une théorie et de techniques leur permettant d'évaluer le caractère probable d'un événement.
Ce n'est qu'au XVIIIe siècle que les statistiques sont utilisées dans un objectif prévisionnel. Buffon, Legendre s'intéressent aux probabilités. Huygens, Bernouilly et Moivre rendent cette branche des mathématiques plus importante en développant son champ d'applications en physique, en biologie …
Au XXe siècle, en 1933, Kolmogorov va formaliser la théorie des probabilités.
L'ordinateur, outil de calcul informatique (apparu dans les années 1940 aux États-Unis et 1960 en Europe) permet de traiter un nombre de données de plus en plus grand, de plus en plus rapidement, de classifier et de faire des calculs complexes, d'analyser les rapports entre des séries de données de types différents. De plus le développement de logiciels de tracés permet aux médias, grâce aux graphiques, de diffuser les résultats statistiques vers le grand public.
Le premier ordinateur

L'ENIAC (acronyme de l'expression anglaise Electronic Numerical Integrator Analyser and Computer), est le premier ordinateur entièrement électronique
Crédit :
DP -Wikipedia
Boutons de commande de l'ENIAC

Crédit :
DP -Wikipedia
Changement d'un des tubes à vide !

Crédit :
DP -Wikipedia
Les probabilités et l'apparition des sondages doivent nous mener à nous poser la question de la fiabilité du sondage comme représentatif d'une réalité :
- Choix de l'échantillon, est-il représentatif de la population que l'on veut étudier ?
- Quelle taille d'échantillon permettra de pouvoir interpréter les résultats ?
Les statistiques, sont de plus en plus utilisées dans des domaines aussi variés que la finance, le marketing, les enquêtes d’opinion (sondages), la maintenance, la logistique, les ressources humaines ou la psychologie, la biologie…
Démocratisation des statistiques
La puissance et la facilité d'utilisation des ordinateurs et des logiciels spécialisés dans le calcul statistique a démocratisé l'utilisation des statistiques. Il est aisé de manipuler un grand nombre de données, effectuer une étude personnelle, quelqu'en soit l'intérêt.
Mais la diffusion généralisée de l'outil informatique n'est pas suivie d'une évolution comparable de la connaissance de l'outil statistique théorique; On fait trop souvent dire n'importe quoi et son contraire aux statistiques.
Efficacité des statistiques
Il est facile de faire calculer à un ordinateur des moyennes, pourcentages, médianes et autres calculs … en revanche il est bien plus compliqué de bien analyser les données de façon efficace et de donner une bonne interprétation des résultats.
Une statistique est une quantité calculée à partir d'un certain nombre d'observations. L'expression "une statistique" indique donc un domaine des mathématiques et indique également le principal objet de "l'étude statistique".
 Une Statistique
Une Statistique
On veut étudier, dans une classe de 33 élèves du lycée , le nombre d'enfants par famille.
Il y a donc 33 familles, on obtient les réponses suivantes :
2 ; 1 ; 1 ; 3 ; 2 ; 2 ; 7 ; 4 ; 1 ; 2 ; 3 ; 1 ; 2 ; 4 ; 3 ; 1 ; 1 ; 1 ; 2 ; 2 ; 1 ; 6 ; 2 ; 2 ; 3 ; 1 ; 1 ; 2 ; 1 ; 3 ; 2 ; 1 ; 3
La variable étudiée est le nombre d'enfants par famille. Les valeurs (différentes) prises par cette variable sont : 1 ; 2 ; 3 ; 4 ; 6 ; 7
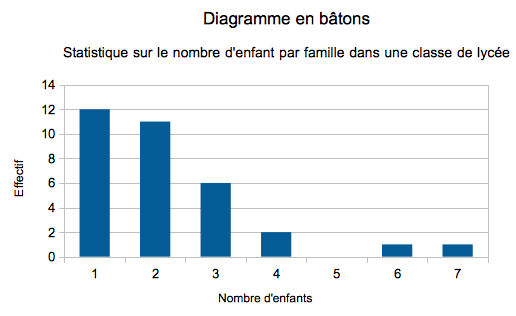
- Nous constatons qu'il y a 12 familles avec 1 enfant : 12 est l'effectif pour la valeur 1 de la variable.
- L'effectif total est la somme des effectifs, c'est dans notre cas 33
Pour mieux visualiser et comprendre les résultats de l'enquête (l'observation), nous allons créer un tableau
Nombre d'enfant - Effectif
| Nombre d'enfants |
1 |
2 |
3 |
4 |
6 |
7 |
| Effectif |
12 |
11 |
6 |
2 |
1 |
1 |
Fréquence d'une valeur
La valeur 3 apparaît 6 fois dans les résultats, sur un total de 33 résultats. La fréquence de la valeur 3 est calculée en faisant le calcul : effectif de cette valeur divisé par l'effectif total. Soit dans notre cas 6/33, c'est à dire environ 0,181, ou encore 18,1 %
Remarquez que la somme de toutes les fréquences est égale à 1.
Effectifs et fréquences cumulées
Notons que le nombre de familles ayant plus de 3 enfants (3 y compris) est : 10. Ce nombre est l'effectif cumulé à partir de la valeur 3 (3 y compris).
- La fréquence cumulée correspondante est 10/33 (soit environ 0,30%)
- L'effectif cumulé sur toutes les valeurs de la variable 1 ; 2 ; 3 ; 4 ; 6 ; 7 est l'effectif total : 33 et donc la fréquence cumulée correspondante : 33/33 = 1
La moyenne
La moyenne de la variable observée est calculée en ajoutant toutes les valeurs de la variable et en divisant par l'effectif total. Pour simplifier on peut effectuer le calcul sur les données classées (groupes de mêmes valeurs) :
moyenne = [(12x1) + (11x2) + (6x3) + (2x4) + (1x6) + (1x7)] /33 = 73 / 33 = 2,12
Le nombre moyen d'enfants par famille pour les 33 familles de cette classe de lycée est 2,12.
La médiane
La médiane de la variable observée est la valeur telle que 50 % des résultats sont supérieurs et 50 % sont inférieurs à cette valeur.
Dans notre cas, l'effectif total est 33, il faut donc trouver la valeur de la variable "nombre d'enfants" telle qu'il y ait autant de familles avant et après cette valeur (soit dans notre cas 16 familles avant et après). Observons le tableau et rangeons les 33 résultats obtenus (données) dans l'ordre croissant (donc 12 fois 1, suivi de 11 x 2 …)
11111111111122222 - (soit 16 valeurs) - 2 - 222223333334467 (soit 16 valeurs)
La valeur médiane de notre étude est 2, il y a 16 familles avant et 16 familles après.
Mode
Le mode d’une série de résultats d'observations est la valeur la plus souvent obtenue : celle qui a la plus grande fréquence, dans notre cas le mode a pour valeur 1.
Pour mieux visualiser et comprendre une étude statistique, utilisons des diagrammes (graphiques). Nous avons utilisé le module Calc (Tableur) de la suite logicielle libre OpenOffice, pour réaliser un diagramme "en bâtons" et diagramme "en camembert" sur la variable étudiée.
Crédit :
UFE@Observatoire de Paris
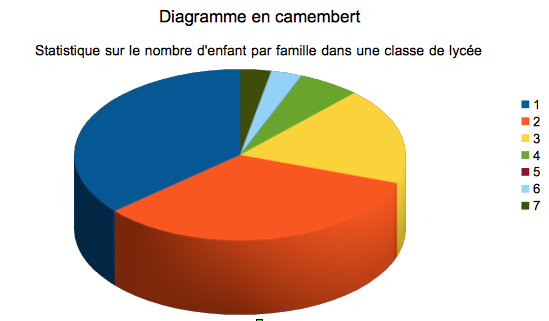
Crédit :
UFE@Observatoire de Paris
Signification du résultat d'une statistique
L'objectif des statistiques est d'étudier à partir d'observations constatées un ensemble d'événements, de phénomènes, les analyser et les mettre en perspective.
Les chiffres sont des outils précis, les mathématiques sont une science exacte. Mais cela ne doit pas faire oublier que le principe de causalité d'un événement, le contexte, le domaine de précision choisi pour les résultats chiffrés, ont un impact sur le résultat de l'analyse.
Pour éviter de dire n’importe quoi, et surtout pour ne pas croire n’importe quoi, il faut avoir un minimum de connaissances de base en statistiques qui nous permettront de répondre, par exemple, aux questions suivantes :
- Quelle est la différence entre un salaire moyen et un salaire médian ?
- Que signifie "il y a une forte corrélation" entre … et …
- Que doit-on comprendre face à une affirmation du style "46 % des personnes interrogées pensent que ..." ?
Moyenne et normalité
Considérons un outil très utilisé dans les études statistique : la moyenne. Souvent, dans la vie courante, on utilise les mots "moyen" et "normal" en leur donnant la même signification. En statistique, la moyenne d'un jeu de donnée ne signifie pas qu'il représente un phénomène normal (dans la norme).
La moyenne est un "indicateur de position" : nombre unique qui caractérise, à lui seul, un grand nombre d'individus ou d'objets … à ne pas confondre avec la normalité, qui revient à interpréter que seuls les individus caractérisés par ce nombre sont dans la normale et les autres sont "anormaux" ! Par exemple :
- On peut calculer quel est le poids moyen dans un population donnée, par exemple les "hommes français de plus de 18 ans", définir un poids "normal" fait intervenir un critère subjectif.
- Faire référence à une "normale" saisonnière en météo veut dire en général les "moyennes" des températures des années précédentes.
- Les enquêtes d'Audimat sur des programmes de télévision sont biaisées quand les choix proposés à l'enquête sont limités à ceux qui plaisent au plus grand nombre.
Hors contexte, le fait de confondre moyenne et normale mène à de fausses conclusions et à des conséquences dans l'usage que l'on fait des statistiques, qui peuvent être utilisée à mauvais escient.
Exact et précis
Il arrive qu'on présente, par exemple, un résultat de sondage en insistant sur la précision des résultats. En effet, il est plus facile d'estimer la dispersion des résultats que leur exactitude, puisqu'on ne sait pas à priori où se trouve le résultat (!).
Question : Vaut-il mieux un résultat précis et faux ou exact et imprécis??
Précis/Exact
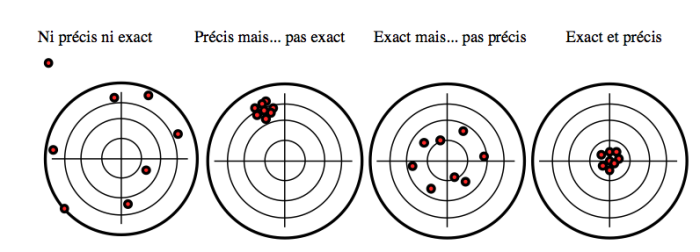
Crédit :
Henri Broch, Cours de Zététique
Cause et corrélation
Attention : Qu'il y ait corrélation entre deux phénomènes ne veut pas dire que l'un est la cause de l'autre.
Le nombre de fleurs dans les champs est corrélé au nombre d'hirondelles mais la pousse des fleurs n'est pas due à la présence des hirondelles ! Les deux phénomènes sont dus à l'arrivée du printemps.
Un coefficient de corrélation élevé n'induit pas obligatoirement une relation de causalité entre les deux phénomènes mesurés. Les deux phénomènes peuvent être corrélés à un même phénomène-source : une troisième variable non mesurée, et dont dépendent les deux autres, comme le montre l'exemple précédent.
Les définitions et les techniques statistiques sont nombreuses et varient selon les domaines dans lesquels elles sont utilisées.
Les notions concernant les variables aléatoires en probabilité sont les mêmes que les notions de variables statistiques en statistique.
Sur un ensemble de N valeurs ou tirages, on peut définir les concepts suivants :
-
Fréquence :
si l'événement A se produit N(A) fois sur les N, la "fréquence de l'événement A" est 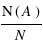
-
Probabilité :
quand le nombre de tirages augmente, on passe de la statistique à la probabilité, on remplace la fréquence par la probabilité de l'événement i, p(i). La somme des N valeurs de p(i) vaut 1: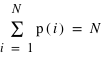
- Les liens entre probabilité et statistique sont forts. Les statistiques partent de la réalité d'une population et cherchent à la modéliser avec des lois mathématiques pour l'expliquer et/ou extrapoler son comportement à une autre population. Les probabilités définissent les lois mathématiques auxquelles obéissent des expériences régies par la hasard.
-
Moyenne arithmétique ou espérance mathématique :
Quand les événements i sont des valeurs numériques, f(i), ou xi
, on définit la Variable Aléatoire (v.a.) X, qui prend les valeurs f(i) avec une probabilité p(i). La valeur moyenne, <f>, ou l'Espérance Mathématique E(X) de la variable X, est 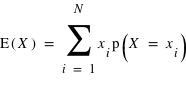
-
Mode, médiane :
A coté de la Moyenne, on peut définir le Mode, qui est la valeur dont la probabilité est le maximum des valeurs p(i). La Médiane est la valeur M qui partage les N valeurs en deux populations de taille égale; La probabilité dans le premier (deuxième) groupe est inférieure (supérieur) à M.
Attention au choix de l'utilisation de l'une ou l'autre de ces valeurs qui peuvent être significativement différentes!
Moyenne, médiane, mode
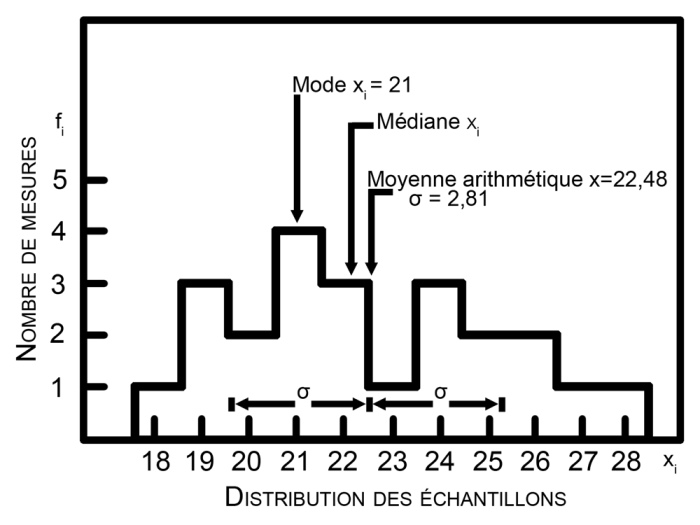
23 échantillons répartis entre 18 et 28, et valeurs de la moyenne, de l'écart-type, de la médiane et du mode.
Crédit :
Observatoire de Paris
-
Loi binomiale :
La loi binomiale est la loi de probabilité de l'expérience de N épreuves à deux choix (gagné/perdu, pile/face...). Si les deux choix ne sont pas équivalents, et que la probabilité de l'un est p , la probabilité de l'autre choix est donc (1-p). On dit qu'il s'agit d'une loi binomiale de paramètres N et p.
La v.a. X qui définit la probabilité d'avoir k fois le choix de probabilité p (et donc N-k fois le choix de probabilité (1-p)), est donnée par 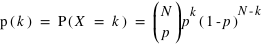 où
où 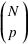 est la combinaison de k éléments parmi N.
est la combinaison de k éléments parmi N.
Quand N devient grand, on remplace la variable aléatoire entière par une variable aléatoire réelle. La loi binomiale devient la loi normale.
-
Combinaisons
Il est important, dans les calculs de statistiques, de savoir combien on peut faire de combinaisons différentes de N éléments.
Par exemple, combien y a-t-il de permutations de 3 éléments, a, b et c ?
Il y a 3 choix pour la première lettre, 2 choix pour la deuxième lettre et 1 seul choix pour la troisième. Le nombre total de choix est 3x2x1 = 6 possibilités : (a-b-c), (a-c-b), (b-a-c), (b-c-a), (c-a-b), (c-b-a).
Combien y a-t-il de classements possibles de 52 cartes? Il y a 52 choix pour la première carte, puis 51 choix pour la deuxième carte, etc.... Le nombre de classements possibles est 52x51x50x49.........x3x2x1 qui s'écrit 52! (factorielle 52)
S'il n'y a que deux sortes d'éléments dans les N, par exemple k fois G (Gagné) et N-k fois P (Perdu), il y aura N! permutations mais beaucoup seront semblables. Combien y aura-t-il de permutations distinctes?
Parmi les N! permutations, celles qui échangent seulement les G sont identiques. Il y a k! permutations de cette sorte. De même, il y a (n-k)! permutations qui sont identiques parce-qu'elles permutent des P.
Il y aura donc 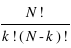 permutations distinctes de N éléments avec k éléments d'une sorte et N-k d'une autre sorte.
permutations distinctes de N éléments avec k éléments d'une sorte et N-k d'une autre sorte.
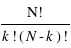 s'écrit
s'écrit 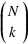
Par exemple, si en tirant 10 fois à Pile ou Face, on trouve 7 Pile et 3 Face, il y a 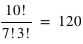 permutations distinctes.
permutations distinctes.
Un autre type de combinaisons est le nombre de "mains" de 13 cartes quand on distribue 52 cartes entre 4 joueurs, au bridge par exemple. Avec le même raisonnement qu'au dessus, on compte 52x51x...43x42x40 soit 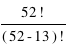 combinaisons possibles si elles sont rangées. Si on ne tient pas compte de l'ordre, il faut diviser par
combinaisons possibles si elles sont rangées. Si on ne tient pas compte de l'ordre, il faut diviser par 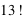 , le nombre de mains avec les mêmes cartes rangées dans des ordres différents. On obtient
, le nombre de mains avec les mêmes cartes rangées dans des ordres différents. On obtient  , soit 635 013 559 600.
, soit 635 013 559 600.
courbe de Gauss
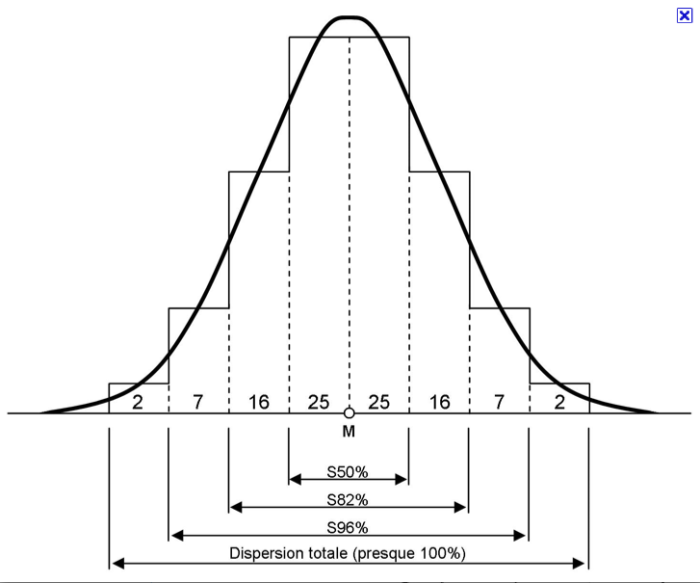
Loi binomiale: l'histogramme représente la de la répartition de 100 probabilités autour de la valeur moyenne M- La courbe superposée est une courbe de Gauss.
Crédit :
wikipédia-Bouterolle
Afin de rechercher s'il y a autre chose que du hasard dans une prédiction (astrologique ou autre), il est possible d'utiliser une technique statistique appelée le test d'hypothèse.
Si un dé est pipé, certaines faces auront plus de chances de sortir que d'autres. Pour savoir si le dé est parfaitement équilibré, il faudrait faire un nombre infini de tirages. Dans la "réalité", on fait un nombre fini de tirages. La technique du test d'hypothèse permet d'interpréter le résultat de ces tirages et de quantifier la qualité du dé.
L'approche par test d'hypothèse consiste à
- calculer, pour N tirages (N grand), la probabilité de tous les résultats possibles en faisant l'hypothèse que le dé est équilibré. Cette hypothèse est appelée l'"hypothèse nulle".
- choisir un seuil de crédibilité, souvent fixé à 5% ou à 1%. Ce seuil définit la limite de confiance, ou seuil de significativité du résultat.
- faire N tirages
- si le résultat trouvé a une probabilité, calculée dans la cadre de l'hypothèse nulle, inférieure à un seuil donné , on rejette l'hypothèse nulle, c'est à dire qu'on décide que le dé est pipé.
- si le résultat a une probabilité supérieure au seuil fixé, cela veut dire que le dé n'est pas pipé. Plutôt que de dire que "le dé est bon", il vaut mieux dire "l'expérience n'a pas permis de montrer que le dé est pipé". En effet, le dé peut être très faiblement déséquilibré.
Dans un test statistique il y a deux façons de se tromper :
- rejeter à tort l'hypothèse nulle lorsqu'elle est vraie (décider que le dé est pipé alors qu'il est équilibré)
- accepter à tort l'hypothèse nulle alors qu'elle est fausse (décider que le dé est bon alors qu'il est pipé). Ce type d'erreur est plus difficile à déterminer (le dé peut être très faiblement déséquilibré).
Utilisation du test d'hypothèse
Les tests d'hypothèse peuvent porter sur la comparaison entre 2 populations, ou comparer la population à un modèle dépendant d'un paramètre. Certaines techniques statistiques permettent de faire une hypothèse sur le paramètre, d'évaluer la probabilité d'observer cette valeur (croyance à priori), puis d'améliorer la valeur de ce paramètre (révision des croyances).
Pour ces études, la population est représentée par un histogramme de fréquences. Le modèle est représenté par une loi de probabilité.
Les tests d'ajustement comparent une population et un modèle.
Voici des exemples de tests d'ajustement.
Les tests d'indépendance servent à savoir si deux variables sont indépendantes.
Exemples de test d'indépendance.
On peut aussi chercher à savoir si deux échantillons proviennent de la même population (tests d'homogénéité).
Exemples de tests d'homogénéité.
Il existe de très nombreux tests statistiques adaptés au domaine dans lequel ils sont utilisés. Ils servent à rejeter ou ne pas rejeter une hypothèse sur une population en testant un jeu de données observées. Il est très important de remarquer que ces tests sont toujours associés à des seuils de confiance qui estiment le risque de se tromper.
Les catégories de tests et la liste des tests usuels sont décrits là.
test du chi-2
Le test du χ
2 (prononcer « khi-deux » ou « khi carré », qu'on écrit également à l'anglaise « chi-deux » ou « chi carré ») est particulièrement utilisé comme test d'ajustement d'une loi de probabilité à un échantillon d'observations supposées indépendantes et de même loi de probabilité.
Son usage est très répandu notamment en génétique où il permet de déterminer, à un seuil donné, la validité d'une hypothèse.
Le test du chi2 fournit une méthode pour déterminer la nature d'une répartition, qui peut être continue ou discrète.
test du chi2
 Pile ou face
Pile ou face
Prenons par exemple l'expérience définie par 1000 tirages à pile-ou-face.
Pour chaque expérience (de 1000 tirages), on note le nombre de tirages « pile ». Ce chiffre est appelé la réalisation de l'expérience.
-
Hypothèse nulle : la pièce est bien équilibrée : Dans ce cas, les 2 faces ont la même probabilité, 0.5, de sortir. Les réalisations se répartissent selon la loi binomiale
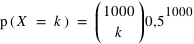 , pour k compris entre 0 et 1000. Cette
distribution gaussienne est centrée sur 500. L'équation de cette courbe "Gaussienne" permet de calculer la probabilité des valeurs pour la réalisation.
, pour k compris entre 0 et 1000. Cette
distribution gaussienne est centrée sur 500. L'équation de cette courbe "Gaussienne" permet de calculer la probabilité des valeurs pour la réalisation.
-
on choisit un seuil de, par exemple, 5%
-
On effectue une expérience :
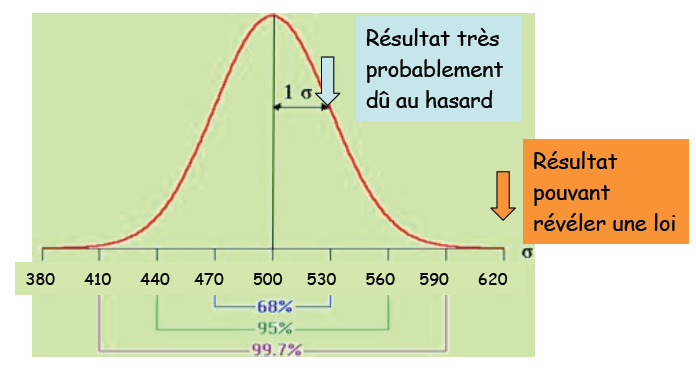
Une réalisation à 530 « pile » (et donc 470 "face") a 16% de chances d’arriver par pur hasard. Ce résultat est donc très probable.
Pour une réalisation à 620 "pile" (et 380 "face"), la probabilité de réalisation dans le cas de l'hypothèse nulle est de 0,003% <5%. L'hypothèse nulle est rejetée: Cela suggère une loi :
La pièce est fausse....
Pile ou face
Crédit :
DP
La statistique est une méthode et une technique, utiliser cet outil mathématique pour étudier une variable sur un jeu de données, consiste à suivre un protocole :
- Collecter des données
- Traiter, analyser les données, avec des outils spécifiques (moyenne, médiane, mode, …, test du chi2)
- Interpréter, expliquer les données (incertitude, biais, limite de confiance, )
Les méthodes statistiques sont maintenant facilement exploitables via l’utilisation de logiciels "libres", à la portée de tous. Voici quelques exemples de logiciels libres et multiplateforme (Mac, Windows, Linux) qui vous permettront de "faire des statistiques à la maison" :
-
R, environnement logiciel libre d'analyse statistique de données et de tracés graphiques
-
Octave, logiciel libre de mathématiques avec des fonctions statistiques, clone de MatLab avec statistiques descriptives
-
Calc de la suite logicielle libre Open Office, tableur permet d'effecteur des calculs statistiques et des tracés graphiques
-
Scilab, logiciel libre de mathématiques : algèbre et statistiques
- …






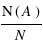
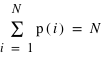
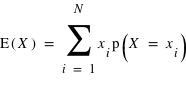

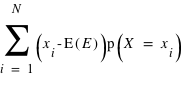 .
.
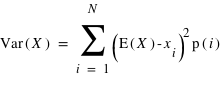 . On peut voir que c'est aussi la différence entre la moyenne des carrés des valeurs et le carré de la moyenne des valeurs,
. On peut voir que c'est aussi la différence entre la moyenne des carrés des valeurs et le carré de la moyenne des valeurs, 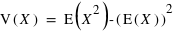
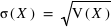 .
.
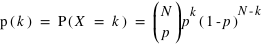 où
où 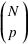 est la combinaison de k éléments parmi N.
est la combinaison de k éléments parmi N.
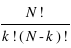 permutations distinctes de N éléments avec k éléments d'une sorte et N-k d'une autre sorte.
permutations distinctes de N éléments avec k éléments d'une sorte et N-k d'une autre sorte.
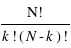 s'écrit
s'écrit 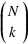
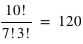 permutations distinctes.
permutations distinctes.
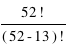 combinaisons possibles si elles sont rangées. Si on ne tient pas compte de l'ordre, il faut diviser par
combinaisons possibles si elles sont rangées. Si on ne tient pas compte de l'ordre, il faut diviser par 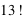 , le nombre de mains avec les mêmes cartes rangées dans des ordres différents. On obtient
, le nombre de mains avec les mêmes cartes rangées dans des ordres différents. On obtient  , soit 635 013 559 600.
, soit 635 013 559 600.

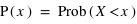 . Donc
. Donc 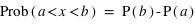 .
.
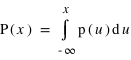 , p(u) s'appelle la densité de probabilité. P(x) est un nombre compris entre 0 et 1. cela correspond aux pourcentages. De plus, il faut que la somme des cas possibles fasse 1, c'est à dire 100%, soit
, p(u) s'appelle la densité de probabilité. P(x) est un nombre compris entre 0 et 1. cela correspond aux pourcentages. De plus, il faut que la somme des cas possibles fasse 1, c'est à dire 100%, soit 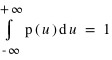
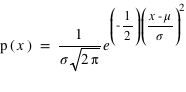 Si la v.a. binomiale X a comme moyenne
Si la v.a. binomiale X a comme moyenne 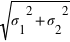 )
)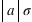 )
)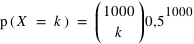 , pour k compris entre 0 et 1000. Cette
, pour k compris entre 0 et 1000. Cette
