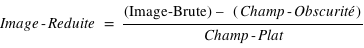Exercice
Exercice
Difficulté : ☆
Quelle sont les objets étudiés par les astronomes ?
Quel est le problème particulier qui se pose à l'astronome pour l'étude des astres ?
Difficulté : ☆
Quelle sont les objets étudiés par les astronomes ?
Quel est le problème particulier qui se pose à l'astronome pour l'étude des astres ?
Difficulté : ☆☆
Quels sont les paramètres qui définissent une onde lumineuse ?
Donnez une définition de ces paramètres
Faites un graphique représentant une onde
Quelles sont les relations mathématiques entre ces paramètres ?
Donner la définition d’une onde électromagnétique.
Quelles sont les unités utilisées pour mesurer une longueur d’onde.
Que représente la fréquence d'une onde lumineuse ?
Quelle est l'unité de mesure de la fréquence ?
Calculer la fréquence 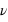 correspondant à une longueur d’onde de
correspondant à une longueur d’onde de 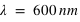
Exprimez le résultat en mètres
Difficulté : ☆
Donner les différents domaines du spectre électromagnétique, faire un schéma en indiquant les longueurs d’onde correspondantes.
Difficulté : ☆☆
Préciser les domaines de longueurs d’onde qui nécessitent des observations par satellite. Expliquer pourquoi.
Préciser les domaines de longueur d’onde accessibles depuis le sol
Expliquer l’intérêt d’observer le même objet à des longueurs d’onde différentes
Préciser quels sont les objets qui émettent le plus dans chaque domaine de longueur d’onde
Donner la définition d’un corps noir
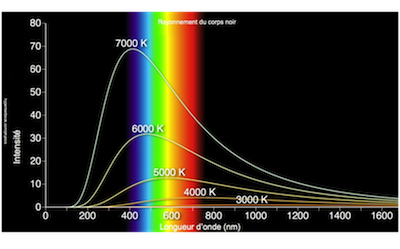
Dans quel domaine de longueur d’onde un corps à une température de 5000 K émet il son maximum d’intensité?
Dans quel domaine un corps à température beaucoup plus basse émet-il son maximum ?
Même question pour un corps à température beaucoup plus élevée.
Wilhem Wien découvrit en 1893, en étudiant les spectres émis par des corps noirs chauffés à différentes températures, la distrinution privilégiée de la lumière autour d''une longueur d'onde caractéristique (pic d'émissivité).
Plus la température est élevée, plus la longueur d'onde du pic d'émissivité est petit, plus la fréquence et l'énergie des photons est grande.
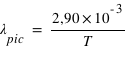
 , longueur d'onde du pic d'émissivité, exprimée en mètre (m)
, longueur d'onde du pic d'émissivité, exprimée en mètre (m)
1nm = 10-9m
T , température, exprimée en Kelvin (K).
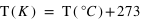
Quelle est la longueur d'onde du pic d'émissivité du corps humain de température 37 °C ?
Calculez la température de surface du Soleil, sachant que son pic d'émissivité est d'environ 500nm dans la partie du spectre correspondant à la lumire verte ?
Dans quelles autres longueurs d'onde le Soleil émet t'il ?
Pourquoi la lumière du Soleil nous parait elle blanche ?
La distribution spectrale de la lumière émise, ou absorbée, par un corps, totalement isolé et maintenau à température constante, ne dépend que de la température du corps. Un tel corps est connu sous le nom de "corps noir". Les lois caractérisant l'état de la lumière dans un corps noir ont été établies à la fois expérimentalement et théoriquement. Elles caractérisent la luminance spectrale énergétique de la source en fonction de la longueur d'onde, la longueur d'onde pour laquelle cette luminance est maximale et la puissance totale rayonnée dans toutes les longueurs d'onde. Chacune de ces grandeurs fait intervenir un seul paramètre physique qui est la température du corps noir.
La luminance spectrale ainsi définie ne dépend plus, pour un rayonnement de corps noir, que de la température T et de la longueur d'onde selon une loi établie par Planck et qui porte son nom :
Les courbes qui décrivent la lumière spectrale d'un corps noirs à différentes températures (en fonction de la longueur d'onde) ont toutes la même forme et sont "emboîtées" les unes dans les autres.

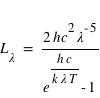
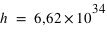 Js, est la constante de Planck
Js, est la constante de PlanckQue décrit la loi de Planck ?
Considérons que l'étoile observée est assez loin pour apparaître comme un point de lumière, qu'elle sera sa couleur apparente en fonction de sa température de surface, par exemple pour les températeures suivantes (T(K), exprimée en Kelvin):
Utilisez la calcultette "Calcotron" en haut de la fenêtre à gauche.
Une source de lumière émet des photons, elle se déplace par rapport à l'observateur.
Calculez la valeur du décalage en longueur d'onde que l'on observe, dans le cas où la lumière émise est de 500 nm (nanomètres) et qu'elle s'éloigne de l'observateur à la vitesse de 6000 km/s. Le décalage est il vers le bleu ou vers le rouge ?
Calculez la valeur du décalage en longueur d'onde que l'on observe, dans le cas où la lumière émise à 500 nm se rapproche de l'observateur à la vitesse de 6000 km/s:.
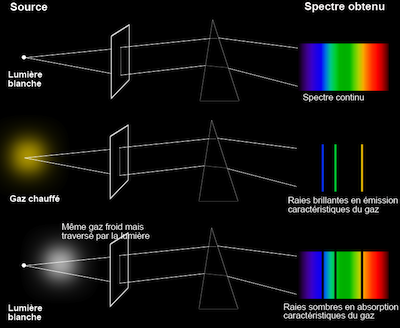
Le type de spectre (continu, raies d'émission, raies d'absorption) caractéristique d'une source correspondent aux conditions décrites par les lois de Kirchhoff (publiée en 1859 en collaboration avec Bunsen).
Difficulté : ☆☆☆
Donner les lois de Kirchhoff.
L'astronomie peut être définie comme l'étude de la lumière qui nous vient du ciel. Les informations dont les astronomes disposent est principalement déduite de l'analyse de la lumière.
Pour analyser la lumière, il faut d'abord la capter.
Caractéristiques et fonctions des télescopes :
Quelle est la taille des plus grands télescopes actuels ?
Difficulté : ☆
info sur la taille des télescopes : qu'est-ce qu'on appelle un eptit télescope
À quoi servent les petits télescopes ?
A quoi servent les télescopes de 4m depuis l’arrivée des 8 -10 m ?
Pourquoi utiliser des télescopes de plus en plus grands ?
Difficulté : ☆
Diamètre des miroirs ?
des 2 télescopes KECK ?
des 4 télescopes VLT
Quel est le principal intérêt du télescope de Schmidt ?
Pourquoi utiliser des télescopes de plus en plus grands ?
Citer cinq grands thèmes dans lesquels les nouveaux instruments permettront de progresser.
rappel spectro ; spectro IR proche, moyen ; OA, interféreométrie …
A quoi sert l’optique adaptative ?
A quoi sert la spectrographie multi-objets ?
A quoi sert l’interférométrie ?
Quels nouveaux phénomènes ont été mis en évidence par les observations X ?
Présentation différents observatoires et télescope : Observatoire de Haute Provence : site exoplanète de l'Observatoire de Paris, observatoire de Radioastronomie de Nançay
Citez une découverte majeure réalisée à partir d'observations au télescope de 1,93m de l'OHP ?
Expliquer quelles mesures spectrales ont permis la découverte.
Quels sont les avantages et les inconvénients des observations spatiales par rapport aux observations sol?
A quoi servent les radiotélescopes ?
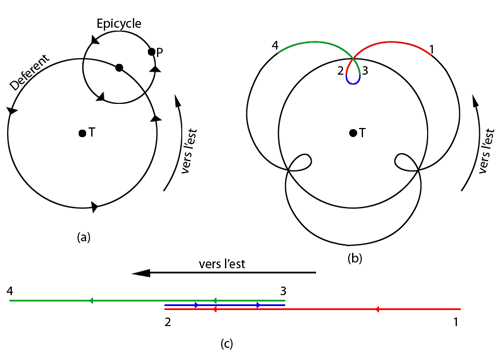
Rappel sur les excentriques, épicycle et mettre le schéma
Difficulté : ☆☆
Vous détaillerez brièvement la théorie des excentriques et des épicycles. Vous indiquerez en quoi l'introduction par Ptolémée du point équant constitue une "tricherie géniale" selon l'expression de Jean-Pierre Verdet.
Difficulté : ☆☆
Quelle est l’organisation de l’Univers chez Aristote ?
Difficulté : ☆☆
Rappeler les circonstances (scientifiques, religieuses et politiques) de la condamnation de Galilée
Difficulté : ☆☆
Quels sont les reproches faits, par les autres savants, à Galilée au sujet de ses observations faites à l’aide de la lunette ?
Difficulté : ☆☆
Vous détaillerez les premières observations de Galilée avec sa lunette. Vous indiquerez pour chacune d'elles en quoi elle constitue un argument en faveur du système copernicien.
Difficulté : ☆☆
Expliquez comment les observations de la Lune, des satellites de Jupiter et des taches solaires, faites par Galilée, lui permettent de défendre le système de Copernic
Nous allons utiliser le logiciel libre (opensource) Stellarium pour reproduire les observations de Galilée à padoue en 1610, à 19H.
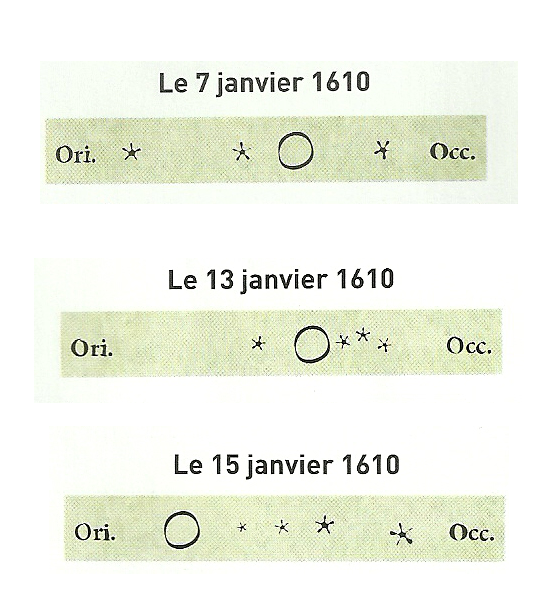

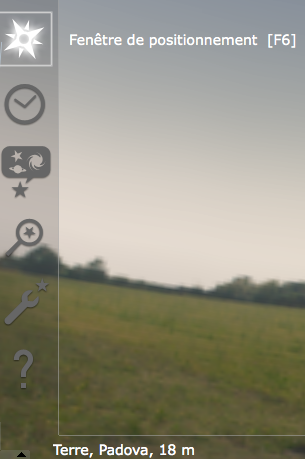
Le récit commence la nuit du 7 janvier 1610 ; l’observation est faite depuis la ville de Padoue en Italie à 19H. Il explore le ciel aux abords de la planète. Jupiter est représenté par un cercle et ses satellites par des étoiles, "Ori" indique l'est et "Occ indique l'ouest.
Les jours suivants, Galilée continue à observer cette région du ciel et il comprend que les astres qu'il a pris pour des "étoiles" tournent autour de Jupiter comme la Lune tourne autour de la Terre.
Et le 13 Janvier, pour la première fois, il aperçoit quatre astres qu'il décrit comme des "petites étoiles"…
Faire le croquis comme Galilée des satellites de Jupiter et de Jupiter pour les observation des 7, 13 et 15 janvier
Pouquoi Galilée n'a t'il représenté que trois satellites sur son dessin du 7 janvier 1610 ?
Décrire les trajectoires de satellites vus de la Terre
Les galaxies sont des ensembles d’étoiles (entre 10 millions et 100 milliards), de gaz et de poussières.
Pour commencer observons la galaxie la plus proche de nous, notre propre Galaxie : La Voie Lactée. L’image ci-dessous est une photographie panoramique de la Voie Lactée. Les trois ingrédients composant les galaxies sont clairement visibles sur cette image.

Le gaz - Le gaz contenu dans la Galaxie (essentiellement de l’hydrogène) se trouve sous plusieurs états. Il existe dans notre Galaxie des grands nuages froids d’hydrogène moléculaire représentant approximativement la moitié de toute la masse de gaz dans la région comprise dans l’orbite du Soleil. C’est au sein de ces nuages que naissent les étoiles par effondrement gravitationnel. La signature spectrale des nuages moléculaires est observable dans le domaine radio millimetrique (raies du monoxyde de carbone CO).
Après leur naissance au sein d’un nuage moléculaire, les étoiles les plus massives ionisent le gaz environnant. Il se forme alors des nuages de gaz ionisé appellés nébuleuses en émission. Sur la photographie, les nébuleuses en émission sont clairement reconnaisables à leur teinte rouge-rose due à la couleur de la raie d’émission de l’hydrogène Halpha à 656.3 nanomètres.
La poussière – Les galaxies contiennent aussi de la poussière que les étoiles ont formée pendant leur vie et qu’elles ont ejecté dans le milieu interstellaire. Ces particules de poussière ont la propriété d’absorber la lumière émise par les étoiles, exactement comme la poussière suspendue dans l’air absorbe la lumière du Soleil. Ainsi, depuis la Terre nous ne pouvons observer (dans le domaine de la lumière visible) qu’une petite partie de notre Galaxie. La poussière distribuée sur le plan de la Galaxie, absorbe une grande partie de la lumière provenant du centre galactique et au delà. Sur la photographie de la Voie Lactée les régions en noir ne sont pas des zones vides d’étoiles et de gaz mais des régions où la poussière a absorbé pratiquement toute la lumière en arrière plan.
L’absorption par la poussière est un effet chromatique : la poussière diffuse beaucoup plus la lumière bleue que la lumière rouge. La poussière eteint et rougit la lumière des objects astrophysiques.
Étoiles, gaz et poussière sont les ingrédients principaux des galaxies. Chacune de ces composantes a sa propre signature spectrale. L’outil fondamental des astronomes extra-galactiques est l’analyse des spectres des galaxies. À partir des spectres, les astronomes réussissent à déterminer :
Mais aussi :
Les questions que vous trouverez au cours de ce TP sur l'analyse des Spectres observés de galaxies vous permettrons d'approcher le travail de l'astrophysicien extra- galactique.
Spectre d’émission - Considérons un nuage chaud et ténu d’hydrogène. Les atomes entrent en collision entre eux, et l’énergie des collisions peut transférer un électron vers un niveau d’énergie supérieur. En retombant l’électron émet un ou plusieurs photons de longueur d’onde propre à l’hydrogène. Dans le domaine visible, le résultat sera un spectre appelé spectre d'émission, car on y voit des raies d’émission.
Spectre thermalisé ou du corps noir - Contrairement au nuage ténu, un corps noir a une densité élevée. Avant de sortir du corps noir les photons créés par les atomes subissent de multiples collisions avec ceux-ci. Ceci a pour effet de redistribuer les photons sur toutes les longueurs d’ondes, donnant ainsi la distribution du corps noir. Lorsqu’on analyse le spectre d’un corps noir on obtient une bande continue de lumière allant du rouge au violet : c’est un spectre continu. Tous les objects en équilibre thermique, c’est à dire caractérisés par une température propre (comme les étoiles), ont une émission voisine de celle d’un corp noir.
Spectre en absorption - Il existe une troisième classe de spectres : les spectres d’absorption. Un spectre d’absorption se forme lorsqu’un faisceau de lumière continue passe par un nuage ténu et froid. Seuls les photons correspondant aux transitions permises sont absorbés par les atomes du nuage puis réémis dans diverses directions. On obtient un spectre continu (corps noir) avec des raies noires correspondant aux absorptions. Le spectre de la lumière solaire est un exemple de spectre d’ émission. Les raies d’absorption se forment quand la lumière du soleil passe les couches ténues de l’atmosphère solaire. On peut ainsi déterminer la composition chimique de l’atmosphère du Soleil.
Difficulté : ☆
En vous aidant de l’introduction, compléter le tableau suivant. Quels sont les objets astrophysiques responsables des différents types de spectres dans une galaxie ?
| Spectre du corps noir | Raies en émission | Raies en absorption |
|---|---|---|
| La lumière continue du spectre d'une galaxie provient … | Les raies d'émissions observées dans le spectre d'une galaxie proviennent … | Les raies d'absoption observées dans le spectre d'une galaxie proviennent essentiellement … |
Le programme Spectrum Explorer permet d’afficher les spectres de divers objets astrophysiques (étoiles, nébuleuses, galaxies, etc..) en représentation 2D (l’image qui sort du spectrographe) et sa représentation en 1D.
Charger le programme Spectrum Explorer, sur le site Project LITE. Ce programme est libre et multiplateforme.
Chargement du spectre de NGC 5236
C’est l’image à la sortie du spectrographe. Le rectangle à droite represente la couleur l’objet vu sans spectrographe. Tout les pixels d’une même colonne ont la même longueur d’onde.
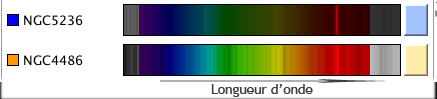
C’est la représentation utilisée par les astronomes avec en abscisse la longeur d’onde en nanomètres et en ordonnée l’intensité de la lumière. Il est possible de changer l’unité en abscisse en fréquences ou énergie dans le menu plot. Rappel : λ=c/ν où λ est la longueur d’onde, ν la fréquence et c la vitesse de la lumière dans le vide.
Revenons au spectre de la galaxie NGC 5236 affiché à l'écran par Spectrum Explorer (spex_v3.jnlp)
Quel(s) type(s) de spectre(s) compose(nt) le spectre de NGC 5236 ?
Que peut on dire sur la composition de cette galaxie?
La couleur d’une galaxie est essentiellement due aux types d’étoiles la composant. En effet, le spectre continu et les raies d’abosrption d’une galaxie proviennent presque exclusivement de la lumière émise par ses étoiles. Ainsi, la lumière qui nous provient d’une galaxie est un mélange de tous les spectres de corps noir émis par les étoiles. En comparant le spectre d’une galaxie à celui d’une étoile, il est possible de trouver le type d’étoile qui la compose majoritairement.
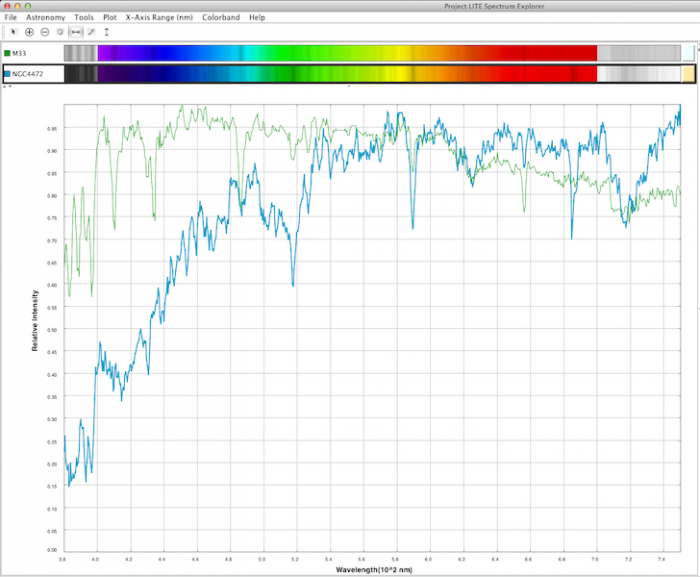
Dans cette partie du TP nous allons comparer le spectre d’une galaxies spirale M33 et d’une galaxie elliptique NGC 4472 et en déduire le type d’étoiles qui les constituent.

Difficulté : ☆
À partir des images des deux galaxies nous pouvons constater que ces deux galaxies ont des couleurs trés différentes. La galaxie spirale est bleutée avec des zones rouge- rose (les nébuleuses d’émissions) alors que la galaxie elliptique est jaune-rouge. Qu'en est-il de leur spectre ?
Utilisez à nouveau le programme spex_v3.jnlp (Project LITE Spectrum Explorer) pour afficher les spectres des galaxies M33 et NGC4472.
Retrouvez-vous la différence de couleur visible sur l’image des galaxies au niveau de leur spectre ?
Remplir le tableau suivant à partir des informations de la figure H- R diagram




En astronomie observationnelle, la réduction de données est très importante car elle permet de corriger des effets instrumentaux des images ou des spectres acquis pendant l'observation.
L'observation astronomique avec une caméra CCD implique 2 principales corrections : le champ plat et le courant d'obscurité.
La correction de champ plat consiste à corriger la réponse non uniforme pixel à pixel d'une matrice CDD. Pour cela on utilise une image (appelée « flat field» ou « champ plat») où l'intensité est quasiment la même partout dans le champ.
Ceci peut être fait en observant le ciel à l'aube ou au crépuscule.
Le courant d'obscurité est un signal que l'on observe même lorsqu'aucune source n'éclaire la matrice CCD.
Son origine est thermique et ne correspond à aucun signal astrophysique. Il faut donc corriger l'image brute de cet artefact en soustrayant à cette image, une image prise dans l'obscurité (champ d'obscurité ou « dark field » en anglais).
Nous avons donc une expression mathématique pour calculer une image réduite, à partir d'une image brute ; soit l' équation de la réduction :
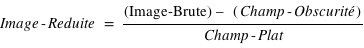
GIRAFFE est un spectrographe multi-objets qui permet l’observation simultanée de 130 objets. Il est monté sur l’un des foyers NASMYTH d’un des télescopes de 8m du VLT (ESO, Chili). Grâce au grand diamètre du VLT, les étoiles des galaxies du Groupe Local telles que celles du Petit Nuage de Magellan situées à 45000 pc de la Terre deviennent alors accessibles à l’observation.
Dans cette étude, des étoiles de magnitude en bande V entre 14 et 18 ont été observées, ce sont principalement des étoiles de type B dont certaines sont binaires spectroscopiques et d’autres Be (B+émission).
Pour réaliser l'exercice suivant vous allez utiliser le logiciel, opensource, de traitement et d'analyse d'images ImageJ et un fichier de données acquises au VLT avec le spectrographe GIRAFFE.
Télecharger le logiciel libre sur le site du Space Telescope Science Institute (STSC) ImageJ
Télécharger l'archive "vltbleu.zip", la décompacter et et Ouvrir le fichier « vltbleunoFF.fits », ce fichier a été corrigé du courant d’obscurité mais pas de la plage de lumière uniforme.
Pour faire apparaître les 130 spectres, vous aller utiliser les outils suivants :
Puis à l’aide de « plot profile » afficher les spectres. Déplacer la ligne et afficher plusieurs spectres.
Comment apparaissent les spectres ?
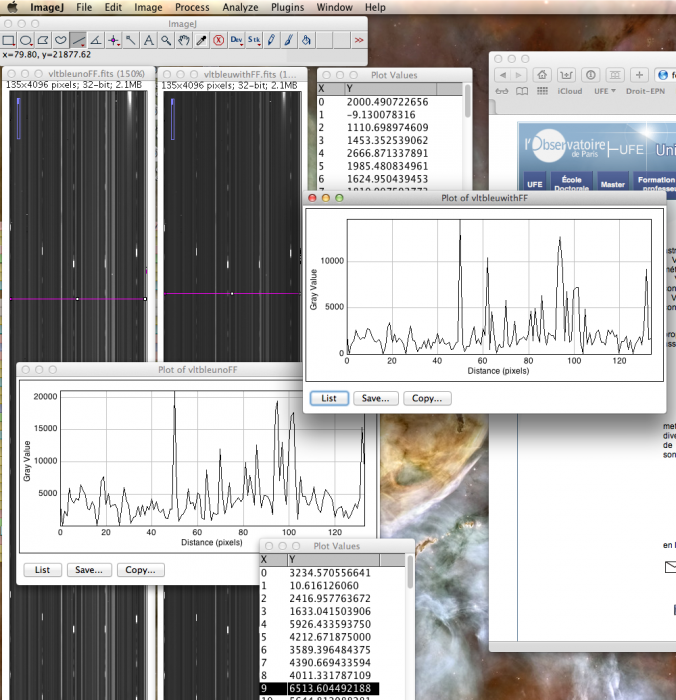


Ouvrir maintenant le fichier « vltbleuwithFF.fits », ce fichier a été corrigé en plus de la plage de lumière uniforme.
De même, faire des coupes, vérifier que les spectres sont maintenant corrigés de la signature instrumentale.
Dans quel sens la longueur d’onde croit (les raies principales sont celles d’hydrogène) ?
Dans quel sens la longueur d’onde croit (les raies principales sont celles d’hydrogène) ?
Les raies sont celles d’étoiles chaudes de température comprises entre 10000 et 35000K (Tsoleil : 6000K). La profondeur des raies varie suivant la température, la gravité de surface des étoiles et leur vitesse de rotation.
Identifier les raies : (hydrogène neutre : Hε, Hδ, Hγ ; Hélium neutre : HeI 4026, HeI 4120, HeI 4143, HeI 4388, HeI 4438, HeI 4471 ; Magnésium 1 fois ionisé : MgII 4481 ; les longueurs d’onde sont en angströms. )
Identifier des étoiles Be, celles-ci ont des raies d’émission qui se superposent aux raies d’absorption des étoiles B.
Quelques infos concernant la réduction de données en spectroscopie.
Nous allons utiliser un logiciel orienté "spectres" : SPLAT. Vous le trouverez ici:
http://astro.dur.ac.uk/~pdraper/splat/splat-vo/ainsi qu'un mode d'emploi (en anglais) :
http://astro.dur.ac.uk/~pdraper/splat/sun243.htx/sun243.htmlLe menu "Operations". permet, entre autre d' afficher plusieurs spectres ensembles, choisir des symboles/couleurs … faire des opérations entre spectres (sauf la médiane malheureusement) ou entre un spectre et une constante …
Calibrer en longuer d'onde : Menu "View" : sélectionner "View/modify spectra values" puis dans la fenêtre qui s'affiche, sélectionner dans "Operations" la fonction "Modify coordinates" (atttention à dé-sélectionner la case "Readonly" avant). Dans la fenêtre qui s'affiche, vous pouvez dans l'onglet "Linear" appliquer un "offset" (longueur d'onde du premier pixel à calculer à partir des fichiers de calibrations de Thorium) et un "scale factor", le nombre d'Ansgtrom par pixel de détecteur . Dans la fenêtre principale, dans le menu "View", sélectionner "view/modify spectral coordinates". Dans la nouvelle fenêtre, selectionner Units: Angstroms (ou autre) puis cliquer sur "Set". Le logiciel sait maintenant que l'axe des X est en A. Un nouveau spectre calibré en longeur d'onde est disponible dans la fenêtre principale.
Superposer un atlas de raies à un spectre : Dans le menu "Options", sélectionner "Line identifiers" puis les catalogues "Optical_absorption_lines" et "Optical_emission_lines" (ou autre, à vous de tester !). Afficher un spectre puis dans la fenêtre principale, panneau de droite cliquer sur la boite "Displayed" pour superposer les catalogues de raies.
Quelques précisions sur le processus de réduction : un spectre de tungstène permet de calculer le flat. Il suffit de soustraire le
biais (ou offset) et de normaliser (diviser par la valeur max)... et donc
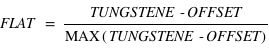


Difficulté : ☆☆
L'objectif de cet exercice est d'approcher de façon simplifiée le traitement des données obtenues par l'observation de l'étoile Hip06999. Donc de "réduire l'image numérique" Hip06999-brute.jpg correspondante.
Cette image est brute (par opposition à réduite, sur laquelle aucune correction n'a été encore effectuée).
Téléchargez sur votre poste de travail le fichier archive Hip06999.zip. Décompressez-le. Il contient les fichiers de travail :
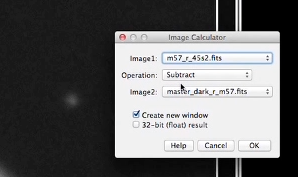
Ouvrez les fichiers flat.jpg et dark.jpg, respectivement champ plat et champ d'obscurité, utilisez les outils de l'application ImageJ pour obtenir l'image réduite de cette étoile binaire en appliquant l'équation de la réduction ci-dessus.
Vous pouvez télécharger le logiciel opensource et multiplateforme ImageJ à l'adresse : http://rsbweb.nih.gov/ij/download.html
menu Process > Image Calculator ...Attention : pour mieux visualiser le résultat :
réhaussez le contraste :
Process > Enhance Contrastaidez-vous des LUT's (look up Tables : tables de couleurs).
menu Image > Lookup Tables ..., ou bien dans la barre des outils : l'outil LUT 4
Comparer l'image brute et l'image réduite.


Nous vous proposons dans ce chapitre une application des concepts scientifiques abordés dans ce site Ondes et Instrument ; il s'agit du traitement des données en astronomie : en particulier la réduction de données acquises au télescope de 80cm de l'Observatoire de Haute Provence lors d'une observation en août 2011.
Il est recommandé de consulter les chapitre "Faire parler la lumière" et "De l'image numérique aux données scientifiques" avant d'entreprendre ce TP.
D'autre part, vous devez :
Vous trouverez également tout ce qui est nécessaire à la réalisation du TP sur le site http://ufe.obspm.fr/reduction (ImageJ, les plugins StackReg et TurboReg. Les données
Si besoin, commencer par des exercices de base : TP - de base.
Pour suivre "pas à pas" le déroulement de l'opération de réduction des données de M57, suivez la procédure dans la vidéo "De l'image numérique aux données scientifiques", au chapitre "Application : réduction de données" (à la minute 8:40 de la vidéo)
Vous pouvez également télécharger la vidéo "De l'image numérique aux données scientifiques", au format QuickTime, (application.mov) : avec le lecteur QuickTime vous aurez accès à la vidéo chapitrée.

La réduction des données d'observation de la nébuleuse de la Lyre (M57), acquises en août 2011 à l'Observatoire de Hautre Provence est réalisée avec le logiciel opensource ImageJ.
Nous allons :
On ne montre, dans la vidéo, la manipulation que sur un des filtres (le travail de réduction, dans la réalité est à effectuer sur chacun des filtres utilisés pour les observations).
Voir le déroulement de la calibration de M57 sur la vidéo : format application.mov ou application.mp4 , le chapitre correspondant aux procédures de réduction de m57 à l'aide du logiciel ImageJ commence au temps t= 8:40 mn.

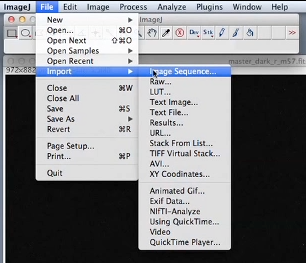
La première étape de la réduction consiste à préparer une image appelée "master-dark".
Nous allons tout d'abord ouvrir l'ensemble des images de calibration prises au télescope pour mesurer le courant d’obscurité : cliquer sur le menu FILE puis sélectionner IMPORT et IMAGE SEQUENCE. Apres s’être assuré que l’on se trouve bien dans le répertoire contenant les données de calibration, il est possible d’entrer une chaîne de caractère contenue dans le nom de toutes les images de courant d‘obscurité, dans notre exemple, « r_45dark », ce qui permet d’ouvrir toutes les images dont le nom contient cette chaîne de caractère en une seule opération.
Le logiciel ouvre toutes les images de courant d'obscurité et les place dans une pile d'images ou STACK, que l’on peut facilement inspecter visuellement grâce au curseur situé en bas de la fenêtre. Dans notre exemple, trois images de courant d’obscurité ont été realisées.
Nous allons répéter la même opération et ouvrir une deuxième pile contenant les mêmes images, que nous allons utiliser pour effectuer quelques tests simples et vérifier qu’elles sont utilisables pour la réduction des données. Nous utiliserons la pile de gauche pour traiter les données prises au télescope, alors que la pile de droite va nous servir à faire nos tests de vérification.

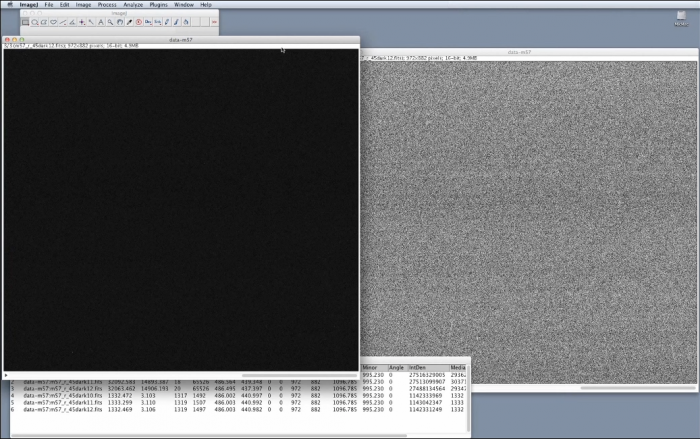

Optimiser le contraste des images de courant d’obscurité afin de vérifier qu’elles ne contiennent pas de défauts importants. Pour cela, cliquer sur PROCESS et ENHANCE CONSTRAST puis normaliser toutes les images en même temps. Cette opération révèle le bruit de photon sur chacune des images. En les inspectant tour à tour, on constate qu’il n’y a pas de différence notable sur l’aspect général du bruit entre les images, ni d’image avec un défaut particulier qui devrait être retirée de la pile.
Vérifier cela quantitativement : cliquer sur PLUGINS, STACKS et MEASURE STACK. Quelques éléments statistiques s’affichent : on peut constater que toutes les images ont à peu près la même valeur moyenne et déviation standard, ce qui confirme qu’il n’y a pas de défauts particuliers.
Répétons la même opération sur les images qui n’ont pas été optimisées en contraste. Nous constatons que la valeur moyenne des images ainsi que leur déviation standard sont beaucoup plus petites que dans les images optimisées en constraste. Ce qui signifie que cette opération modifie les données.
Il faudra donc faire attention à utiliser des images qui n’ont pas été modifiées pour effectuer la réduction des données, sinon le résultat sera fausse par cette manipulation.
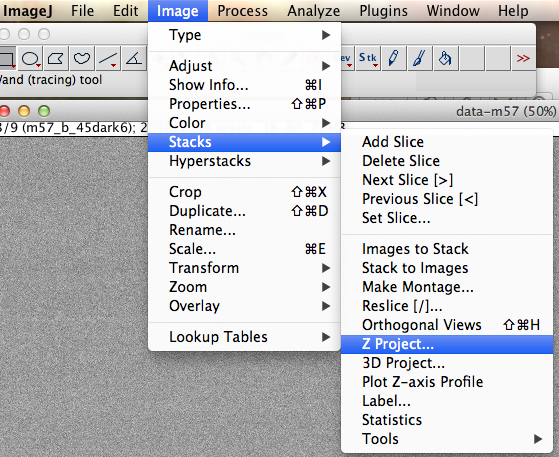
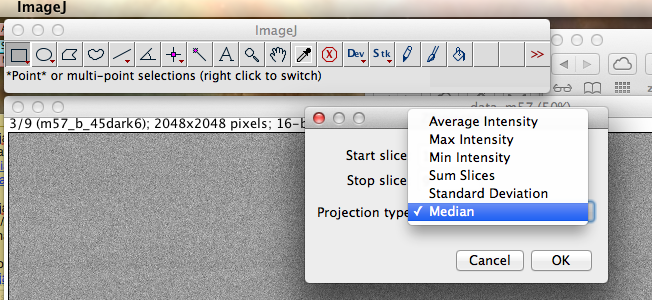
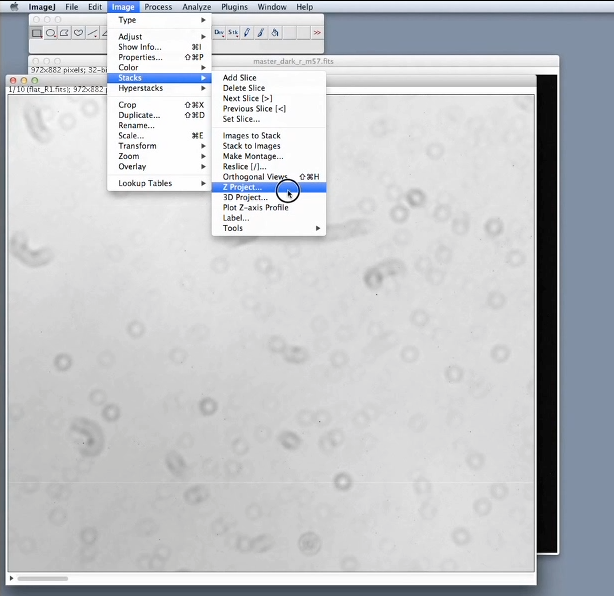
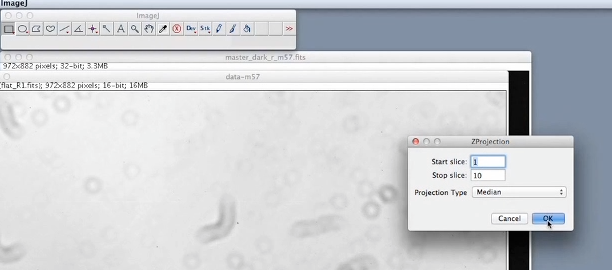
Nous pouvons maintenant construire une image de courant d'obscurité maître ou master-dark.
Pour cela cliquer sur IMAGE, STACKS et ZPROJECT. Vérifier que la méthode de combinaison est bien la médiane : le logiciel va calculer l’image médiane des trois images de courant d’obscurité et l’afficher. Cliquer à nouveau sur ANALYZE et MEASURE : nous voyons que la nouvelle image est bien représentative de la moyenne entre les images individuelles et que sa dispersion standard a diminue, ce qui montre que le bruit de photon a bien été diminue par cette opération. Plus il y a d’images individuelles, plus la réduction du bruit sera efficace. Dans cet exemple seulement trois images ont été prises, ce qui limite la réduction de bruit.
Nous devons maintenant sauvegarder notre image de courant d’obscurité maître en cliquant sur FILE SAVE AS et FITS. La réduction peut être un processus mettant en jeu de nombreux fichiers différents et il est important de bien classer ses fichiers. Dans cet exemple nous mettrons tous les fichiers produits dans un dossier appele RESULTS pour les distinguer des fichiers correspondants aux images prises au télescope. Il est egalement important d’utiliser des noms de fichier explicites ce qui aidera par la suite à ne pas confondre les différentes images.
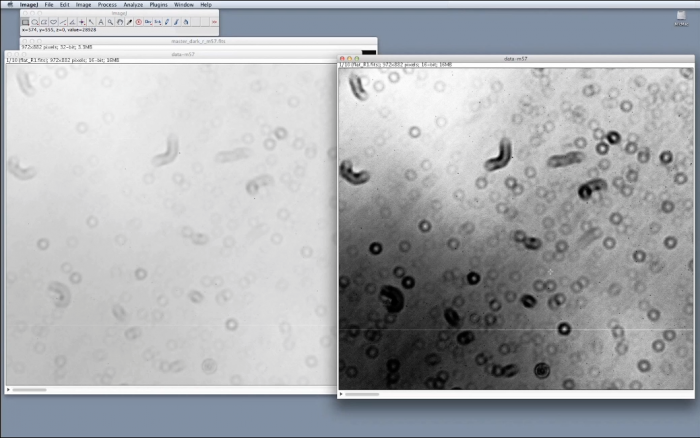
La deuxième étape consiste à construire l’image de champ plat maître ou "master-flat". Comme dans la première étape, nous allons ouvrir l'ensemble des images de champ plat prises au télescope : cliquer sur le menu FILE puis sélectionner IMPORT et IMAGE SEQUENCE.
Apres s’être assuré que l’on se trouve bien dans le répertoire contenant les données de calibration : entrer une chaine de caractère contenue dans le nom de toutes les images de champ plat. Dans notre exemple, « flat_R ». Toutes les images de champ plat sont ouvertes dans une pile. Nous voyons dans notre exemple que dix images de champ plat ont été réalisées.
Nous allons ouvrir une deuxième pile contenant les mêmes images pour les inspecter. Sans modifier les images de la première pile qui seront utilisées pour la réduction proprement dite. Nous allons commencer par optimiser le contraste des images afin de vérifier qu’elles ne contiennent pas de défauts importants : cliquer sur PROCESS et ENHANCE CONSTRAST puis normaliser toutes les images en même temps.
En les inspectant tour à tour, on constate qu’il n’y a pas de différence notable sur l’aspect général des images, ni d’image avec un défaut particulier qui devrait être retirée de la pile. Nous voyons clairement apparaitre plusieurs types de défauts :
Les anneaux sombres sont dûs à des poussières qui se trouvent sur les différents éléments optiques du télescopes ou de l’instrument. Nous voyons aussi des gradients de lumière en arrière plan qui peuvent être dus à des effets de vignettages, c'est-à-dire d’ombre ; ou aux pixels du détecteur qui réagissent de manière différente à une même intensité de lumière. Enfin, certaines lignes du détecteur sont défectueuses et ne permettent plus de transférer le signal correctement. Elles apparaissent sous la forme de lignes blanches ou noires.
Nous pouvons maintenant construire une image de champ plat maître ou master-flat. Pour cela cliquer sur IMAGE, STACKS et ZPROJECT. Verifier à nouveau que la méthode de combinaison est bien la médiane : le logiciel va calculer l’image médiane des dix images de courant d’obscurité et l’afficher. Il est important de ne pas oublier que la mesure de champ plat contient également le courant d’obscurité qu’il faut donc retirer.
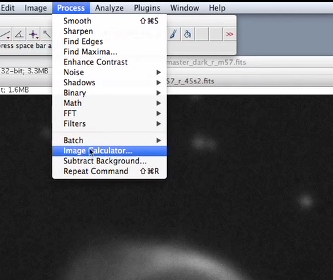
Pour cela cliquer sur PROCESS et IMAGE CALCULATOR. Sélectionner l’image médiane que nous venons de calculer et soustraire l’image de courant d’obscurité maître. Nous devons maintenant normaliser cette image à 1 :
Entrer la valeur maximale mesurée à l’étape précédente et valider. L’image de champ plat maître est prête.
Pour la sauvegarder, cliquer sur FILE SAVE AS et FITS.
Prenez garde à bien sauvegarder cette image dans le bon répertoire à lui donner un nom de fichier explicite. Nous pouvons maintenant fermer les fenêtres devenues inutiles pour la suite des opérations pour nous préparer à la réduction proprement dite.
Le processus de réduction peut se résumer en une équation trés simple appelée "Équation fondamentale de la réduction" : 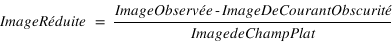
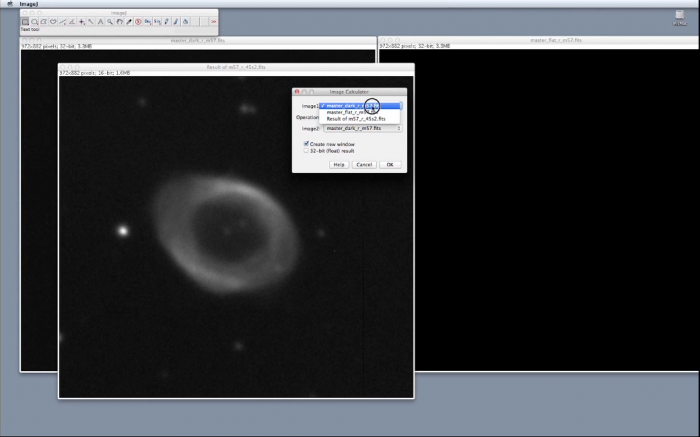
Commencer par ouvrir l’image scientifique brute à réduire en cliquant sur FILE et OPEN. Revenir au répertoire où se trouvent les données collectées au télescope et sélectionner l’image à traiter.


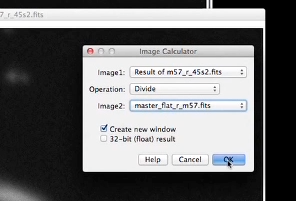
Cliquer sur PROCESS et IMAGE CALCULATOR.
Sélectionner l’image que nous venons de calculer et diviser par l’image de champ plat maître.
Sélectionner l’image à réduire puis soustraire l’image de courant d’obscurité maître ; nous vous conseillons de fermer l’image brute pour éviter toute confusion par la suite.
L’image réduite s’affiche. Fermer à nouveau le résultat intermédiaire précédent pour éviter toute confusion. Nous pouvons également fermer les images de calibration maître, sauf si d’autres images dans la même bande doivent être réduites.
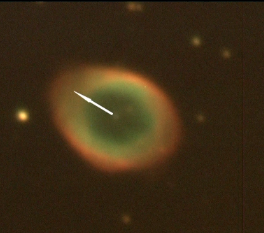
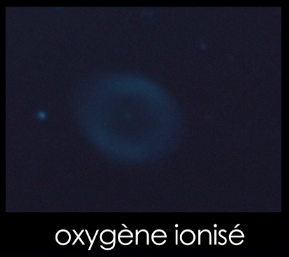
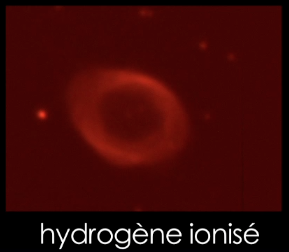

Nous avons maintenant une image scientifique réduite qui a été corrigée des défauts du détecteur et de l’instrument. Elle est prête à être exploitée scientifiquement.
Pour cela nous devons la sauvegarder en cliquant sur FILE SAVE AS puis FITS. Penser a nouveau a bien sauvegarder cette image dans le bon répertoire a lui donner un nom de fichier explicite.
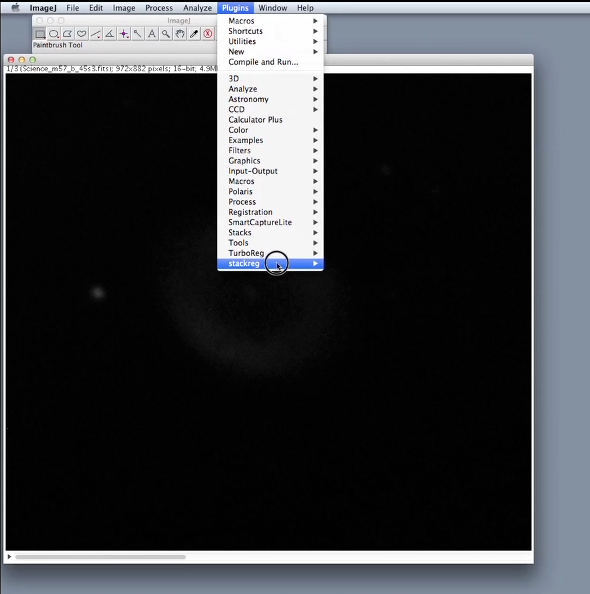

Nous avons vu comment réduire l’image brute d’un objet dans une bande d’observation donnée. Nous allons maintenant voir comment combiner différentes bandes pour former une image couleur en trois bandes.
Cliquer sur FILE, IMPORT et IMAGE SEQUENCE pour ouvrir les images de l'objet observé dans différentes bandes.
Jusqu'à présent nous avons réduit ensemble l’image de M57 en bande R, nous avons préparé les images scientifiques réduites de M57 dans les bandes B et V en suivant la même méthode.
Les images réduites de M57 en bandes B, R et V s’affichent dans une même pile que nous pouvons inspecter visuellement. Nous constatons que les 3 images ne sont pas correctement alignées : les étoiles présentent dans le champ apparaissent a différentes positions sur chacune des images de la pile. Il faut donc tout d’abord réaligner les trois images.
Cliquer sur PLUGINS, STACKREG et a nouveau STACKREG, sélectionner une transformation par translation qui donne les meilleures résultats. Le logiciel réaligne automatiquement les images. Si nous inspectons à nouveau la pile, les étoiles apparaissent maintenant à la même position sur l’image.
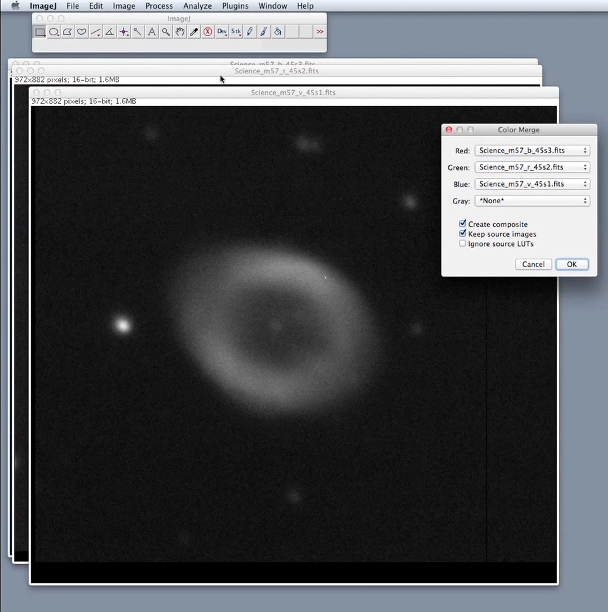
Nous allons maintenant pouvoir combiner les trois images (en associant un canal de couleur (R,V (comme Vert) et B) à un filtre (filtre bande B, R et V comme Visible) :
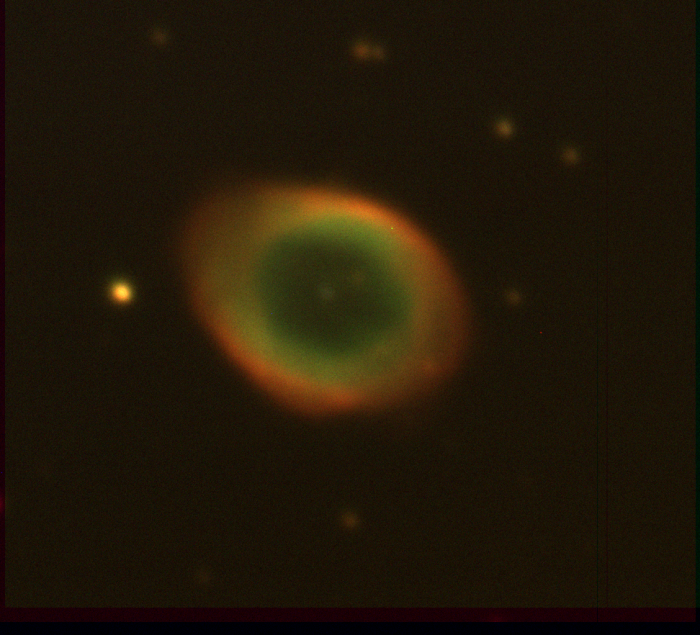
Noter que dans cet exemple, les trois filtres correspondent aux couleurs primaires ce qui permet de faire une synthèse additive des couleurs et ainsi reproduire une véritable image couleur qui reproduit l’objet quasiment comme notre œil "le verrait".
Rien n’empêche d’associer aux trois cannaux de couleur des filtres différents correspondants à des rayonnements qui peuvent même être invisibles à l’œil et produire ainsi des images en fausses couleurs. Les images que l’on voit dans les magazines ne sont donc pas forcément réalistes !
pages_exercices-ondes/corps-noir.html
pages_exercices-instruments/yeux-artificiels.html
pages_exercices-ondes/astronome.html
L'astronomie est la science de l'observation des astres. Les astronomes cherchent à expliquer leur origine, leur évolution, leurs propriétés physiques (mouvement, forme) et chimiques (composition) : ils sont astrophysiciens.
Leur extrême éloignement ne permet (quasiment pas) pas d’étude in situ : l'astronome n'a pas sont objet d'étude à "portée de main", ni d'œil d'ailleur).
L’analyse des rayonnements électromagnétiques qu’ils émettent rend leur étude possible.
Voir la vidéo Lumière! Lumière !
pages_exercices-ondes/exercices-ondes.html
Sa longueur d’onde 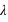 ou sa fréquence
ou sa fréquence 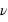 et son intensité
et son intensité 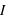 .
.
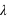 est la distance entre deux maxima de l’onde électromagnétique.
est la distance entre deux maxima de l’onde électromagnétique. 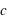 étant la vitesse de la lumière dans le vide, longueur d'onde et fréquence sont liées par la relation mathématique
étant la vitesse de la lumière dans le vide, longueur d'onde et fréquence sont liées par la relation mathématique 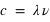
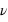 est le nombre d'oscillations de l’onde électromagnétique par seconde, elle est mesurée en Hertz
est le nombre d'oscillations de l’onde électromagnétique par seconde, elle est mesurée en Hertz
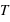 est la durée d’une pulsation
est la durée d’une pulsation 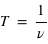 (mesurée en seconde)
(mesurée en seconde)L' onde électromagnétique est la représentation des rayonnements électromagnétique : c'est une oscillation couplée du champ électrique et du champ magnétique qui se propage à la vitesse de la lumière.
La lumière désigne un rayonnement électromagnétique visible par l'œil humain. Les ondes radio, les rayons 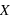 et
et 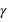 sont aussi des rayonnements électromagnétiques.
sont aussi des rayonnements électromagnétiques.
Toutes les unités de longueur, mais dans le domaine optique on l’exprime en Angstrom ou en nanomètre, 1 Angstrom valant 0,1 nanomètre, soit 10-10 mètre.
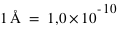 m
m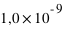 m
mC'est le nombre d'oscillations de l’onde électromagnétique par seconde, elle est mesurée en Hertz, noté Hz
Attention aux unités 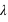 et
et 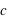 (on prendra pour la célérité de l'onde lumineuse,
(on prendra pour la célérité de l'onde lumineuse, 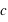 la vitesse de la lumière :
la vitesse de la lumière : 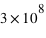 m/s)
m/s)
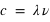 , donc
, donc 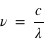
où, exprimés en mètres 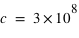 m et
m et 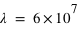 m
m
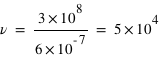 Hz
Hz
pages_exercices-ondes/spectre-electromagnetique.html
Rayons γ : 10-14 m ↔ Rayons X : 1012 m ↔ Ultra Violet (UV) : 10-10 ↔ 400 nm : VISIBLE : 750 nm ↔Infra Rouge (IR) : 10-14 ↔ Radio : 106
La lumière visible est un rayonnement électromagnétique, mais ne constitue qu'une petite partie du spectre électromagnétique.
pages_exercices-ondes/spectre-electromagnetique.html
En raison de la présence de l’atmosphère terrestre qui absorbe certaines longueurs d’onde, seules des observations par satellite permettent de détecter les domaines gamma, X , UV et infrarouge (certaines fenêtres dans l’infrarouge peuvent être détectées depuis le sol).
Le domaine visible, l’infrarouge proche et la radio ne sont pas absorbées par l’atmosphère elles sont donc accessibles depuis le sol.
Un même objet émet généralement dans un spectre étendu de longueurs d’ondes. Chacun des composants ou régions de l’objet observé émet à différentes longueurs d’onde, l’observer à différentes longueurs d’onde permet donc d’explorer ses composants et ses différentes zones.
Les objets présentant des phénomènes physiques violents émettent principalement dans le domaine γ et X (étoiles à neutron). Les étoiles jeunes émettent principalement dans le domaine UV, les étoiles d’âge moyen dans le domaine visible, les poussières dans l’IR, les nuages moléculaires dans le millimétrique et le gaz neutre des galaxies dans le domaine radio à 21cm.
pages_exercices-ondes/corps-noir.html
En physique, un corps noir désigne un objet idéal dont le spectre électromagnétique ne dépend que de sa température. En pratique, un tel objet matériel n'existe pas, mais il représente un cas idéalisé servant de référence pour les physiciens. Contrairement à ce que son nom suggère, un corps noir n'apparaît pas forcément noir. En effet l'adjectif «noir» signifie ici que l'objet lui- même absorbe toute la lumière extérieure qui tomberait sur lui, et ne reflète aucune radiation. La seule radiation provenant du corps noir est la radiation thermique, ne dépendant que de la température.
Dans le domaine visible.
Dans le domaine infrarouge ou radio.
Dans le domaine ultraviolet, X ou gamma.
pages_exercices-ondes/loi-wien.html
On considère le corps humain comme un corps noir et on applique l'équation de Wien :
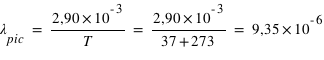 m, soit
m, soit 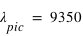 nm
nm
Cette longueur d'onde se trouve dans le domaine de l'infrarouge du spectre électromagnétique.
pages_exercices-ondes/loi-wien.html
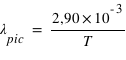 , on a donc
, on a donc 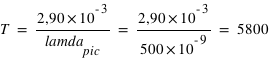 K
K
La température du Soleil est d'environ 5800 K
bla
pages_exercices-ondes/loi-planck.html
La loi de Planck décrit la répartition de l'énergie électromagnétique rayonnée par un corps noir à une température donnée, en fonction de la longueur d'onde.
bla
pages_exercices-ondes/codes-lumière.html
La couleur apparente d'une étoile (assez loin pour être considérée comme une source lumineuse ponctuelle), correspondant à :*******
pages_exercices-ondes/redshift.html
Rappel : Chaque élément chimique peut émettre ou absorber une série de longueur d'ondes caractéristiques. Cependant les observations en laboratoire et au télescope donnent des résultats différents selon que la source est au repos ou se déplace par rapport à l'observateur. On constate qu'au télescope la série émise ou absorbée présente un décalage en logueur d'onde. Ce décalage est du à l'effet Doppler.
Le décalage des raies spectrales 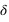 est calculé à partir de la longueur d'onde observée (
est calculé à partir de la longueur d'onde observée (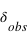 ) et de la longueur d'onde "normale" (
) et de la longueur d'onde "normale" (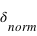 )obtenue en laboratoire pour une source au repos.
)obtenue en laboratoire pour une source au repos.
On utilisera la formule : 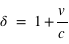
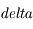 représente la valeur du décalage Doppler
représente la valeur du décalage Doppler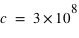 m/s est la vitesse de la lumière dans le vide
m/s est la vitesse de la lumière dans le vide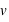 la vitesse de la source par rapport à l'observateur
la vitesse de la source par rapport à l'observateur
Et la formule : 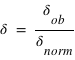
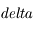 représente la valeur du décalage Doppler
représente la valeur du décalage Doppler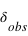 longueur d'onde observée
longueur d'onde observée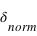 longueur d'onde en laboratoire (source au repos)
longueur d'onde en laboratoire (source au repos)
La source s'éloigne de l'observateur donc : 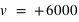 km/s
km/s
On utilisera les formules : 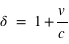 et
et 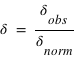
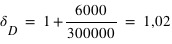 , la longueur d'onde observée sera
, la longueur d'onde observée sera 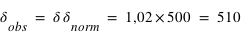 nm
nm
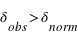 , la valeur de la longueur d'onde a augmenté, il y a donc décalage vers le rouge
, la valeur de la longueur d'onde a augmenté, il y a donc décalage vers le rouge
La source s'éloigne de l'observateur donc : 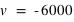 km/s
km/s
On utilisera les formules : 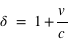 (approximation si on ne tient pas compte des effets de la relativité restreinte, et
(approximation si on ne tient pas compte des effets de la relativité restreinte, et 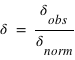
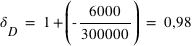 , la longueur d'onde observée sera
, la longueur d'onde observée sera 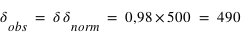 nm
nm
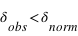 , la valeur de la longueur d'onde a augmenté, il y a donc décalage vers le bleu
, la valeur de la longueur d'onde a augmenté, il y a donc décalage vers le bleu
pages_exercices-ondes/rayonnement.html
pages_exercices-instruments/yeux-artificiels.html
Les petits télescopes sont utilisés pour mener des campagnes d'observations systématiques sur de grandes zones du ciel ou permettent de consacrer de nombreuses heures d'observation pour la recherche d’objets particuliers comme les exoplanètes.
Ces télescopes sont maintenant dédiés à des grands relevés.
Ils établissent des catalogues d’objets faibles (astéroïdes, étoiles, galaxies etc...) à différentes longueurs d’ondes afin que des études complémentaires de ces objets puissent être réalisées avec des télescopes de plus grande taille.
Ils permettent d’observer des objets de plus en plus faibles avec une résolution spatiale de plus en plus grande.
pages_exercices-instruments/yeux-artificiels.html
10 m
8 m
pages_exercices-instruments/yeux-artificiels.html
Ce télescope est caractérisé par un miroir primaire sphérique qui permet d’observer un champ plus grand, de l’ordre de 6 degrés carrés alors qu’avec des miroirs habituels le champ est de l’ordre de quelques minutes d’arc. Cette particularité fait que les télescopes de Schmidt ont principalement été utilisés pour cartographier l’ensemble du ciel.
pages_exercices-instruments/yeux-artificiels.html
Ils permettent d’observer des objets de plus en plus faibles avec des résolutions spatiales de plus en plus grandes.
pages_exercices-instruments/yeux-artificiels.html
L’optique adaptative permet de corriger les effets de la turbulence atmosphérique.
La spectroscopie multi objets permet d’obtenir simultanément le spectre d’un grand nombre d’objets dans un même champ. Il est possible d’observer plusieurs centaines d’objets ce qui permet un gain de temps considérable par rapport à l’époque où les spectrographes n’observaient qu’un objet à la fois. Ainsi l’étude d’objets composés de nombreux éléments comme les amas globulaires ou les amas de galaxies a beaucoup progressé.
L’interférométrie permet d’accroître le pouvoir de résolution spatiale d’un seul télescope en combinant les images obtenues par plusieurs télescopes associés. L'interférométrie est utilisée en astronomie aussi bien avec des télescopes optiques qu'avec des radiotélescopes. Son avantage est de permettre une résolution équivalente à celle d'un miroir (ou radiotélescope) de diamètre équivalent à l'écart entre les instruments combinés.
Détection de gaz chaud dans lesquels baignent les amas de galaxies
Noyaux actifs de galaxies, trous noirs.
pages_exercices-instruments/voir-invisible.html
La première exoplanète a été détectée en 1995 par l’équipe de M. Mayor et D. Queloz avec le 1,93 mètre de l’OHP équipé du spectromètre ELODIE. C'est l'étoile 51 Pegasi qui a montré la première "exoplanète".
quelques photos du télescope et de spectro (voir stages DU)
La période de révolution de la planète autour de son étoile.
La rotation de la planète invisible autour de l’étoile induit une variation de la position de l’étoile dont la vitesse varie en fonction de la position de la planète. La mesure de la variation au cours du temps du décalage spectral des raies du spectre de l’étoile permet de calculer la période de révolution de la planète autour de son étoile.
Avantages : pas de turbulence atmosphérique – observation de toutes les longueurs d’ondes (de gamma à radio). Inconvénients : Petits télescopes, durée limitée des mission, pas de réparation possible (sauf Hubble).
Les radiotélescopes permettent de révéler des objets ou des composants de certains objets invisibles à d’autres longueurs d’ondes. Ils permettent surtout d’observer le composant le plus répandu dans l’univers : l’hydrogène neutre qui émet à la longueur d’onde de 21 cm. L'astronomie millimétrique permet d'observer les molécules complexes présentes dans le milieu interstellaire.
pages_exercices-galilee/exercices-galilee.html
pages_exercices-galilee/exercices-galilee.html
Division de l'Univers entre Sublunaire (imparfait, corruptible, soumis aux changements) et le supralunaire (parfait, éternel...). Organisation de sphères enchassées les unes dans les autres.
pages_exercices-galilee/exercices-galilee.html
Mise à l'index du "De Revolutionibus" de Copernic. Demande du pape à Galilée de ne pas présenter la nouvelle organisation du monde comme étant la seule, Pression des Jésuites et du Roi d'Espagne sur le Pape (lutte avec les protestants)
pages_exercices-galilee/satellites-galileens.html
Le simulateur Stellarium montre qu'Europe est juste devant Io et qu'il cache Io. Donc les satellites Callisto - Europe (qui cache Io) – la planète Jupiter – et le satellite Ganymède.
Placez-vous dans le référentiel jupitérien pour mieux comprendre les observations vues de la Terre
pages_tp-ondes/exercices-spectres-1.html
| Spectre du corps noir | Raies en émission | Raies en absorption |
|---|---|---|
| La lumière continue du spectre d'une galaxie provient des étoiles. Les étoiles sont des corps noirs presque parfaits. Le spectre continu d’une galaxie correspond au mélange de tous les corps noirs émis par les milliards d’étoiles. | Les raies d'émissions observées dans le spectre d'une galaxie proviennentdu gaz. Dans le domaine visible, les raies d’émission proviennent du gaz chaud ionisé par les étoiles massives (nébuleuse d’émission ou région HII). | Les raies d'absoption observées dans le spectre d'une galaxie proviennent essentiellement des atmosphères stellaires. |
pages_tp-ondes/exercices-spectres-2.html
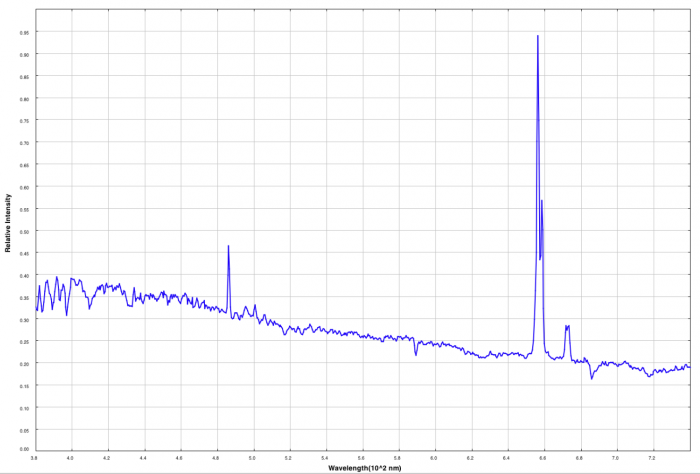
Dans le spectre de NGC 5236 nous pouvons observer :
pages_tp-ondes/exercices-spectres-2.html
La galaxie NGC 5236 contient une importante quantité de gaz chaud, comme le témoigne les raies intenses en émission. Elle contient aussi des étoiles (ouf) détectables par le spectre continu et les raies d’absorption.
pages_tp-ondes/composition-en-etoiles.html
Pour afficher les spectres des galaxies en deux dimensions et au dessous en une dimension :
à écrire plus précisemment : observer ce qu'affiche le programme ==> interprétation
Oui. Le continu de M33 est beaucoup plus intense que NGC 4472 dans la partie bleue du spectre. M33 est donc plus bleu que NGC 4472.
pages_tp-traitement/giraffe.html
Ces raies d’émission sont plus larges que les raies d’émission d’origine nébulaire liées aux nuages de gaz sur la ligne de visée.
pages_tp-traitement/hip06999.html
En astronomie observationnelle, la réduction de données est très importante car elle permet de corriger des effets instrumentaux des images ou des spectres acquis pendant l'observation. L'observation astronomique avec une caméra CCD implique 2 principales corrections : le champ plat et le courant d'obscurité.
La correction de champ plat consiste à corriger la réponse non uniforme pixel à pixel d'une matrice CCD. Pour cela on utilise une image (appelée « flat field » ou « champ plat» ) où l'intensité est quasiment la même partout dans le champ. Ceci peut être fait en observant le ciel à l'aube ou au crépuscule.
Le courant d'obscurité est un signal que l'on observe même lorsqu'aucune source n'éclaire la matrice CCD. Son origine est thermique et ne correspond à aucun signal astrophysique. Il faut donc corriger l'image brute de cet artefact en soustrayant à cette image, une image prise dans l'obscurité ( champ d'obscurité ou « dark field » en anglais).