On trouvera dans ce chapitre les exercices suivants :
- Détermination de l'équation d'évolution du champ de densité de l'univers
- Effet de l'aplatissement aux pôles du potentiel gravitationnel terrestre
Auteur: Jérôme Thiébaut
Le CMB (Cosmic Microwave Background où fond diffus cosmologique) représente le champ de densité de l'univers lorsque celui ci avait environ 300 000 ans (dans le cadre de la théorie du Big Bang). L'un des enjeux de la cosmologie est, à partir de ce champ de densité, de comprendre son évolution et la formation des structures à différentes échelles (galaxies, amas, super amas, filaments).
Dans un premier temps, on peut linéariser les équations régissant le mouvement d'un fluide afin de déterminer l'évolution linéaire du champ de densité.
Le but de l'exercice est de déterminer l'équation différentielle à laquelle obéit le champ de densité dans ce régime.
Le fond diffus cosmologique vu par COBE et WMAP.
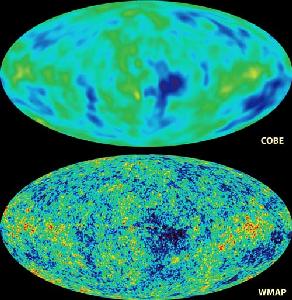
Cartes du ciel obtenues par les satellites COBE (en haut) et WMAP (en bas); on remarque la résolution spatiale bien meilleure de WMAP.
Crédit :
COBE/WMAP
Auteur: Jérôme Thiébaut
 Perturbations linéaires
Perturbations linéaires
Difficulté : ☆☆
Temps : 1 h
Les équations fondamentales gouvernant le mouvement d'un fluide sont:
- l'équation d'Euler (conservation de l'impulsion)
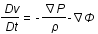
- l'équation de conservation (dans ce cas, conservation de la masse)
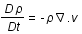
- l'équation de Poisson (reliant masse et potentiel gravitationnel)
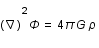 .
.
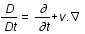 est la dérivée convective (variation totale dûe à la variation temporelle,
est la dérivée convective (variation totale dûe à la variation temporelle, 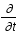 , et spatiale,
, et spatiale, 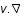 , du fluide) , v la vitesse du fluide, P sa pression,
, du fluide) , v la vitesse du fluide, P sa pression, 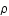 sa densité, G la constante de gravitation et
sa densité, G la constante de gravitation et 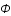 le potentiel gravitationnel.
On souhaite tout d'abord linéariser les équations autour d'un fond homogène,
le potentiel gravitationnel.
On souhaite tout d'abord linéariser les équations autour d'un fond homogène, 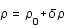 ,
, 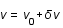 ,
, 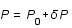 et
et 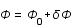 .
.
Question 1)
Réecrire les trois équations linéarisées au premier ordre.
Les perturbations étant faibles, les termes contenant des produits du type  (ordre 2) sont négligeables.
(ordre 2) sont négligeables.
Question 2)
Soustraire à ces équations les équations à l'ordre 0 (c.à.d. les équations non perturbées où les  sont nuls) et les exprimer en fonction du contraste de densité
sont nuls) et les exprimer en fonction du contraste de densité 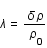
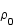 est homogène, son gradient est donc nul. De même pour
est homogène, son gradient est donc nul. De même pour 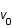 .
.
Question 4)
La vitesse du son 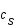 est par définition
est par définition 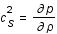 .
Dériver l'équation de conservation afin de déterminer l'équation différentielle du deuxième ordre régissant l'évolution de
.
Dériver l'équation de conservation afin de déterminer l'équation différentielle du deuxième ordre régissant l'évolution de 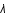 .
.
Auteur: Arnaud Beck
A l'ordre zéro, le potentiel gravitationnel de la Terre est supposé être celui d'une masse ponctuelle située au centre de la terre. Cette hypothèse revient en fait à supposer que la symétrie sphérique de la Terre est parfaite et donc, que son potentiel gravitationnel 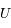 ne dépend que de la distance au centre
ne dépend que de la distance au centre 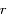 . Or, des mesures suffisamment précises ont montré que des effets "non sphériques" étaient détectables. Cet exercice propose d'étudier la fonction du potentiel terrestre corrigé au premier ordre. Cette correction est celle qui est due à l'aplatissement de la Terre aux pôles et rend le potentiel dépendant de la latitude.
. Or, des mesures suffisamment précises ont montré que des effets "non sphériques" étaient détectables. Cet exercice propose d'étudier la fonction du potentiel terrestre corrigé au premier ordre. Cette correction est celle qui est due à l'aplatissement de la Terre aux pôles et rend le potentiel dépendant de la latitude.
Voici un autre exercice sur le potentiel gravitationnel terrestre.
Auteur: Arnaud Beck
 Potentiel gravitationnel terrestre
Potentiel gravitationnel terrestre
Difficulté : ☆
Temps : 1h
Question 1)
Sachant que le champ de gravitation est donné par le gradient du potentiel 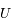 , donner les composantes radiale et tangentielle de ce champ.
, donner les composantes radiale et tangentielle de ce champ.
En coordonnées polaires, les composantes du gradient sont données par 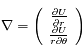
Question 2)
En symétrie parfaitement sphérique, le champ gravitationnel de la Terre est non nul en tout point de l'espace. Il est intéressant de noter que ce n'est pas le cas si l'on prend en compte l'aplatissement de la Terre. Déterminer les points en lesquels le champ gravitationnel s'annule. D'un de point de vue mathématique, que sont ces points pour la fonction 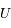 ?
?
Le champ gravitationnel s'annule si ses deux composantes sont nulles au même point.
Question 3)
Voici une représentation de 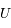 en niveau de gris. Le cercle blanc centrale est une zone où le potentiel diverge et n'est pas évalué. Il ne faut donc pas en tenir compte. En faisant des coupes sur cette image, déterminer la variation de
en niveau de gris. Le cercle blanc centrale est une zone où le potentiel diverge et n'est pas évalué. Il ne faut donc pas en tenir compte. En faisant des coupes sur cette image, déterminer la variation de 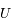 dans les directions radiale et tangentielle au niveau des points critiques. En déduire si ces points sont des minima, des maxima ou des points selles.
dans les directions radiale et tangentielle au niveau des points critiques. En déduire si ces points sont des minima, des maxima ou des points selles.


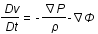
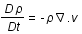
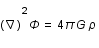 .
.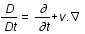 est la dérivée convective (variation totale dûe à la variation temporelle,
est la dérivée convective (variation totale dûe à la variation temporelle, 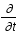 , et spatiale,
, et spatiale, 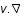 , du fluide) , v la vitesse du fluide, P sa pression,
, du fluide) , v la vitesse du fluide, P sa pression, 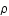 sa densité, G la constante de gravitation et
sa densité, G la constante de gravitation et 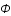 le potentiel gravitationnel.
On souhaite tout d'abord linéariser les équations autour d'un fond homogène,
le potentiel gravitationnel.
On souhaite tout d'abord linéariser les équations autour d'un fond homogène, 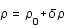 ,
, 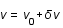 ,
, 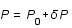 et
et 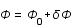 .
.
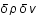 (ordre 2) sont négligeables.
(ordre 2) sont négligeables.
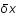 sont nuls) et les exprimer en fonction du contraste de densité
sont nuls) et les exprimer en fonction du contraste de densité 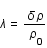
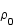 est homogène, son gradient est donc nul. De même pour
est homogène, son gradient est donc nul. De même pour 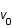 .
.
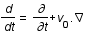 . Ces équations sont écrites en coordonnées eulériennes x(t) (système de coordonnées fixes). On se propose maintenant de les écrire en coordonnées comobiles, r(t), système de coordonnées qui évolue et se dilate avec l'expansion de l'universafin de s'en affranchir. Le passage de l'une à l'autre se fait par:
. Ces équations sont écrites en coordonnées eulériennes x(t) (système de coordonnées fixes). On se propose maintenant de les écrire en coordonnées comobiles, r(t), système de coordonnées qui évolue et se dilate avec l'expansion de l'universafin de s'en affranchir. Le passage de l'une à l'autre se fait par:
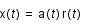 et
et 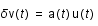 où
où 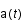 est le facteur d'échelle caractérisant l'expansion et
est le facteur d'échelle caractérisant l'expansion et 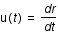 est la vitesse particulière du fluide.
On peut montrer que
est la vitesse particulière du fluide.
On peut montrer que 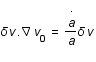 . Réecrire les équations d'Euler et de conservation en fonction de a et u(t).
. Réecrire les équations d'Euler et de conservation en fonction de a et u(t).
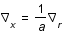
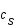 est par définition
est par définition 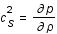 .
Dériver l'équation de conservation afin de déterminer l'équation différentielle du deuxième ordre régissant l'évolution de
.
Dériver l'équation de conservation afin de déterminer l'équation différentielle du deuxième ordre régissant l'évolution de 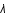 .
.
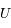 ne dépend que de la distance au centre
ne dépend que de la distance au centre 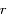 . Or, des mesures suffisamment précises ont montré que des effets "non sphériques" étaient détectables. Cet exercice propose d'étudier la fonction du potentiel terrestre corrigé au premier ordre. Cette correction est celle qui est due à l'aplatissement de la Terre aux pôles et rend le potentiel dépendant de la latitude.
. Or, des mesures suffisamment précises ont montré que des effets "non sphériques" étaient détectables. Cet exercice propose d'étudier la fonction du potentiel terrestre corrigé au premier ordre. Cette correction est celle qui est due à l'aplatissement de la Terre aux pôles et rend le potentiel dépendant de la latitude.
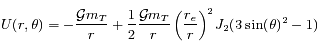
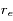 est le rayon équatorial de la Terre,
est le rayon équatorial de la Terre, 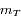 sa masse,
sa masse, 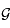 la constante de gravitation,
la constante de gravitation, 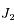 un coefficient de correction sans dimension,
un coefficient de correction sans dimension, 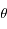 la latitude et
la latitude et 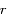 la distance au centre.
la distance au centre.
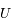 , donner les composantes radiale et tangentielle de ce champ.
, donner les composantes radiale et tangentielle de ce champ.
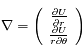
 ?
?
 en niveau de gris. Le cercle blanc centrale est une zone où le potentiel diverge et n'est pas évalué. Il ne faut donc pas en tenir compte. En faisant des coupes sur cette image, déterminer la variation de
en niveau de gris. Le cercle blanc centrale est une zone où le potentiel diverge et n'est pas évalué. Il ne faut donc pas en tenir compte. En faisant des coupes sur cette image, déterminer la variation de 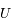 dans les directions radiale et tangentielle au niveau des points critiques. En déduire si ces points sont des minima, des maxima ou des points selles.
dans les directions radiale et tangentielle au niveau des points critiques. En déduire si ces points sont des minima, des maxima ou des points selles.

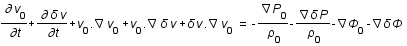
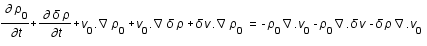
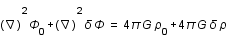
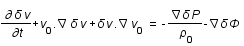
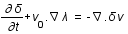
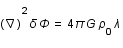
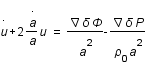
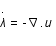
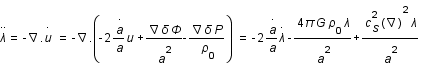
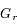 et
et 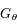 du champ gravitationnel sont données par
du champ gravitationnel sont données par
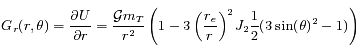
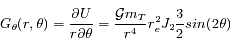
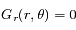 a pour solution
a pour solution 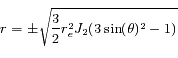
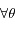 tel que
tel que 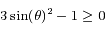
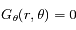 a pour solution
a pour solution ![\theta=0[\frac{\pi}{2}]](../pages_deriv-part/equations_deriv-part/equation58.png)
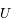 sont donnés par l'intersection de ces deux solutions, soit les points
sont donnés par l'intersection de ces deux solutions, soit les points 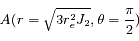 et
et 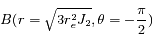
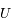 comme celle ci:
comme celle ci:
