Alain Vienne
Les mouvements de Jupiter et de Saturne sont très proches d'un mouvement képlérien. En effet, chacune de ces planètes est principalement attirée par le Soleil mais très peu par l'autre planète (la masse du Soleil est 1047 fois celle de Jupiter et 3498 fois celle de Saturne; ces 2 planètes étant les plus massives du système solaire). Leurs éléments d'orbite, notamment le demi-grand axe, l'excentricité (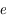 ) et la direction du péricentre (
) et la direction du péricentre (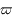 ), sont quasi constants. Plus précisément, soit ils varient peu (oscillations rapides de faible amplitude), soit ils varient lentement ("variations séculaires"). On dit que l'influence de Jupiter sur le mouvement de Saturne est une perturbation (et vice versa) du mouvement képlérien. L'objet de la mécanique céleste dans le cas de systèmes perturbés, est de modéliser ces variations.
), sont quasi constants. Plus précisément, soit ils varient peu (oscillations rapides de faible amplitude), soit ils varient lentement ("variations séculaires"). On dit que l'influence de Jupiter sur le mouvement de Saturne est une perturbation (et vice versa) du mouvement képlérien. L'objet de la mécanique céleste dans le cas de systèmes perturbés, est de modéliser ces variations.
Laplace (1749-1827) avait déjà montré que les demi-grands axes des planètes n'avaient pas de variations séculaires (plus précisément: à un certain degré d'approximation, les demi-grands axes des planètes n'ont que des petites variations périodiques). Ce qui était, à l'époque, un argument fort en faveur de la stabilité du système solaire.
Il fallait quand même s'assurer que les excentricités n'atteignent pas de valeurs trop grandes. En effet, de grandes excentricités conduisent vite à des collisions! L'objet de cette application est de voir que les variations d'excentricités sont bornées.
On simplifie notablement le calcul et la compréhension en utilisant la variable complexe suivante:
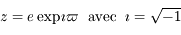
Par exemple, on verra dans l'exercice suivant que l'"execntricité complexe" 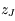 asssociée à Jupiter a le mouvement suivant:
asssociée à Jupiter a le mouvement suivant:
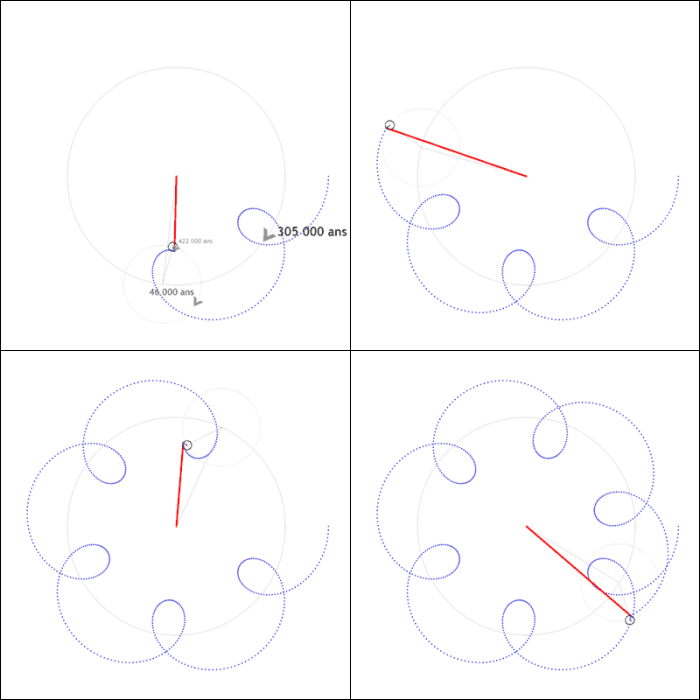
"Excentricité complexe" de Jupiter (
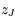
) qui montre que l'exentricité de Jupiter est bornée.
Auteur: Alain Vienne
 Exercice
Exercice
Difficulté : ☆
Temps : 1h30
Question 1)
La partie linéaire des équations séculaires relatives à 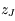 (Jupiter) et à
(Jupiter) et à 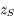 (Saturne) peut s'écrire:
(Saturne) peut s'écrire:
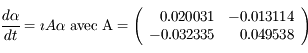
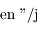
avec 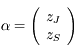
Montrer que 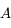 est diagonalisable et donner ses valeurs propres (appelées ici, "fréquences propres").
est diagonalisable et donner ses valeurs propres (appelées ici, "fréquences propres").
Remarque: on notera les valeurs propres 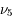 et
et 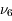 . Ces indices 5 et 6 font référence respectivement à la cinquième et à la sixième ligne de la matrice obtenue par Le Verrier lorsque celui-ci considérait les 8 planètes.
. Ces indices 5 et 6 font référence respectivement à la cinquième et à la sixième ligne de la matrice obtenue par Le Verrier lorsque celui-ci considérait les 8 planètes.
Question 2)
Intégrer le système différentiel en recherchant pour 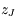 et
et 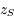 une solution sous la forme de termes périodiques. On montrera que les valeurs propres de la matrice
une solution sous la forme de termes périodiques. On montrera que les valeurs propres de la matrice 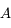 sont les fréquences de ces termes périodiques.
sont les fréquences de ces termes périodiques.
Utiliser le fait que le système est diagonalisable pour définir un nouveau jeu de variables (qui seront les "éléments propres"). On utilisera formellement la matrice des vecteurs propres mais il est inutile de la calculer explicitement.
Question 3)
Donner les périodes de ces termes périodiques en années.
Question 4)
Sachant qu'à 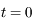 , on a les valeurs:
, on a les valeurs:
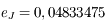 et
et 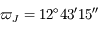
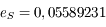 et
et 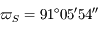
calculer les constantes d'intégration de la solution, puis les amplitudes des termes à très longues périodes des solutions de  et
et  (on ne demande pas les phases)
(on ne demande pas les phases)
Question 5)
En déduire les valeurs extrêmes que peuvent atteindre les excentricités de Jupiter et de Saturne.
 Remarque
Remarque
Le fait que le système de Laplace-Lagrange conduit à des valeurs bornées de l'excentricité est illustré par la figure suivante. C'est la variable 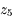 qui est représentée.
qui est représentée.
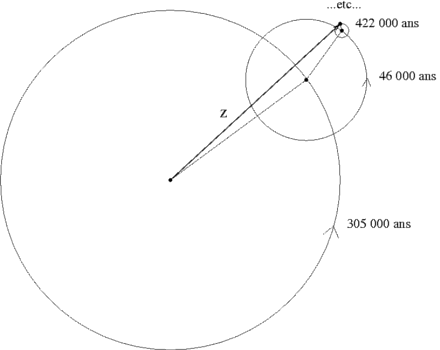
Solution de la variable en excentricité de Jupiter (
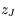
) issue d'un système séculaire complet (non linéarisé et avec les 8 planètes).
Cette solution diffère de la notre car elle est issue d'un système séculaire complet, c'est à dire non linéarisé et avec les 8 planètes.
Auteur: Alain Vienne
Beaucoup de modèles dynamiques, après maintes transformations (hypothèses simplificatrices, moyennisations, ...), ressemblent au modèle du pendule (masse à une distance constante d'un point fixe sous l'effet de la pesanteur). Ici nous allons nous intéresser à un type d'équation du pendule correspondant à l'équation de Mathieu:
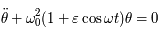
Si 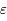 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 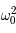 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 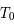 est alors
est alors 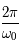 .
.
Ici 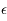 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
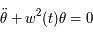
où 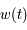 est une fonction périodique de période
est une fonction périodique de période 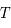 qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
De manière plus ludique, ces équations peuvent modéliser le mouvement d'une balançoire dont le passager se lève et s'assied (périodiquement) afin de s'élancer. Le fait de se lever et de s'assoir régulièrement revient à déplacer le centre de gravité du passager et donc, revient à faire varier périodiquement la longueur du pendule (ici la balançoire).
L'exercice qui suit ne résoud pas l'équation différentielle. Il cherche simplement à savoir dans quelles conditions la solution est bornée ou non (problème de stabilité). Il est insipré du théorème de Gustave Floquet (1847-1920). C'est un exercice de la théorie des équations différentielles mais il utilise beaucoup l'algèbre linéaire d'où sa présence dans cette partie.
Cet exercice est un classique de la théorie des équations différentielle. On le trouve donc dans la partie "Equations différentielles linéaires". Cependant il utilise beaucoup l'algèbre linéaire d'où sa présence dans cette partie.
Auteur: Alain Vienne
 Exercice
Exercice
Difficulté : ☆☆
Temps : 2h30
Voir l'énoncé
Marc Fouchard
L'animation ci-dessous illustre le mouvement diurne du Soleil au dessus de l'horizon en un point de latitude 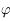 . Le point
. Le point 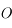 correspond à l'observateur. Il observe le mouvement du Soleil au cours d'une journée. Ce mouvement correspond uniquement à un changement de direction dans laquelle le Soleil est observé. Ainsi on peut représenter ce mouvement par un point se déplaçant sur une sphère (sphère céleste) centrée sur
correspond à l'observateur. Il observe le mouvement du Soleil au cours d'une journée. Ce mouvement correspond uniquement à un changement de direction dans laquelle le Soleil est observé. Ainsi on peut représenter ce mouvement par un point se déplaçant sur une sphère (sphère céleste) centrée sur 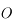 est de rayon qu'on prendra arbitrairement égale à 1.
est de rayon qu'on prendra arbitrairement égale à 1.
Sur cette sphère, on peut représenter toutes les directions parallèles à l'horizon, ce qui défini l'horizon céleste. Les astres dont la direction se trouve en dessous de l'horizon céleste ne sont pas visibles depuis 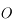 .
Sur l'horizon céleste on peut représenter les directions du Sud
.
Sur l'horizon céleste on peut représenter les directions du Sud 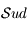 , de l'Ouest
, de l'Ouest 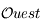 , du Nord
, du Nord 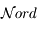 et de l'Est
et de l'Est 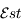 .
De même, on peut représenter la direction perpendiculaire à l'horizon: le Zénith (
.
De même, on peut représenter la direction perpendiculaire à l'horizon: le Zénith (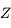 ) et la direction parallèle à l'axe de rotation de la Terre: le pôle céleste Nord (
) et la direction parallèle à l'axe de rotation de la Terre: le pôle céleste Nord (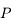 ). Le plan qui coupe la sphère céleste perpendiculaire à la direction
). Le plan qui coupe la sphère céleste perpendiculaire à la direction 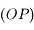 et passant par
et passant par 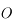 , s'appelle l'équateur céleste. Sur l'équateur céleste on note
, s'appelle l'équateur céleste. Sur l'équateur céleste on note 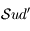 la direction du Sud. On note
la direction du Sud. On note 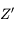 le Nadir, qui correspond à la direction opposée au Zénith, et on note
le Nadir, qui correspond à la direction opposée au Zénith, et on note 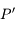 le pôle céleste Sud qui correspond à la direction opposée au pôle céleste nord. On remarquera que les points
le pôle céleste Sud qui correspond à la direction opposée au pôle céleste nord. On remarquera que les points 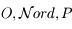 et
et 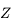 sont coplanaires avec
sont coplanaires avec 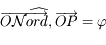 .
.
Ainsi, au cours d'une journée la Terre tourne autour d'un axe parallèle à 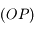 . Pour l'observateur, ceci ce traduit par un déplacement des astres observés sur des cercles parallèles à l'équateur céleste.
. Pour l'observateur, ceci ce traduit par un déplacement des astres observés sur des cercles parallèles à l'équateur céleste.
Soit 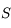 le point de la sphère céleste indiquant la direction dans laquelle est observé le Soleil depuis
le point de la sphère céleste indiquant la direction dans laquelle est observé le Soleil depuis 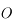 . On appelle
. On appelle 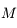 l'intersection de l'arc de grand cercle
l'intersection de l'arc de grand cercle 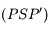 avec l'équateur céleste et
avec l'équateur céleste et 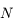 l'intersection de l'arc de grand cercle
l'intersection de l'arc de grand cercle 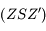 avec l'horizon céleste.
avec l'horizon céleste.
On note 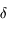 l'angle
l'angle 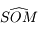 ,
, 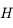 l'angle
l'angle 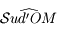 ,
, 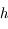 l'angle
l'angle 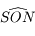 et
et 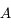 l'angle
l'angle 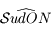 .
. 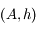 sont appelées les coordonnées locales, alors que
sont appelées les coordonnées locales, alors que 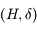 sont les coordonnées horaires. Au court du mouvement diurne d'une étoile seule
sont les coordonnées horaires. Au court du mouvement diurne d'une étoile seule 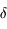 est constant. Pour le Soleil
est constant. Pour le Soleil 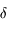 varie au cours de l'année, mais on peut le considérer constant sur une journée. L'animation permet de modifier
varie au cours de l'année, mais on peut le considérer constant sur une journée. L'animation permet de modifier 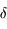 afin de voir les variations dans le mouvement diurne en fonction de
afin de voir les variations dans le mouvement diurne en fonction de 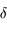 .
.
Le but de cette exercice est d'établir des relations entre les coordonnées horaires et locales par des rotations puis d'utiliser ces relations pour calculer les heures de lever et de coucher du Soleil aux solstices et aux équinoxes.

Auteur: Marc Fouchard
 Exercice
Exercice
Difficulté : ☆☆
Temps : 1h
Question 8)
En déduire les valeurs de l'angle horaire 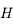 au moment du lever et du coucher du Soleil en fonction de
au moment du lever et du coucher du Soleil en fonction de 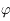 et
et 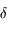 .
.
Marc Fouchard
Les étoiles doubles correspondent à des couples d'étoiles reliées gravitationnellement l'une à l'autre. Ainsi, les deux étoiles effectuent un mouvement elliptique autour du centre de gravité du couple. La détermination des paramètres de cette ellipse, et en particulier de son demi-grand axe, est particulièrement importante parce qu'elle permet d'obtenir la masse des étoiles.
L'objet de ce petit exercice est juste d'établir le système permettant de déterminer les paramètres de l'équation algébrique d'une conique.
Auteur: Marc Fouchard
 Etoiles doubles
Etoiles doubles
Difficulté : ☆
Temps : 20 mn
Question 1)
Quelle est l'équation générale d'une conique dans le plan.
Question 2)
Pour une ellipse, on a la contrainte supplémentaire que 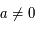 (entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
(entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
Question 3)
On a donc cinq paramètres indépendants à déterminer. Combien, au moins, nous faut-il d'observation pour pouvoir déterminer les paramètres ?
Question 4)
Soit 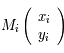 ,
, 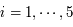 , ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
, ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
Question 5)
Donner une astuce pour se ramener à la résolution d'un système à trois inconnues que l'on déterminera.
Il faut pour cela choisir un repère orthormé dans lequel les coordonnées de 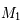 et
et 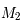 sont les plus simples possibles.
sont les plus simples possibles.
-
Question 1
Solution :
Par définition on a 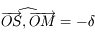 . Les points
. Les points 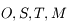 et
et 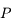 sont coplanaires, ainsi
sont coplanaires, ainsi 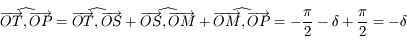 .
.
On a 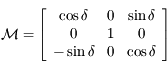 .
.
-
Question 2
Solution :
Par définition 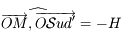 . Comme
. Comme 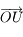 est orthogonal à
est orthogonal à 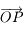 , on en déduit que
, on en déduit que  se trouve sur l'équateur céleste (par définition de l'équateur céleste). De même,
se trouve sur l'équateur céleste (par définition de l'équateur céleste). De même, 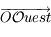 est perpendiculaire au plan
est perpendiculaire au plan 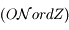 qui est confondu avec le plan
qui est confondu avec le plan 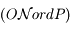 . Ainsi
. Ainsi 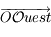 est orthogonal à
est orthogonal à 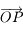 , donc le point
, donc le point 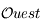 se trouve aussi sur l'équateur céleste. Finalement, les points
se trouve aussi sur l'équateur céleste. Finalement, les points 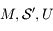 et
et 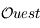 sont sur l'équateur céleste. On a donc:
sont sur l'équateur céleste. On a donc: 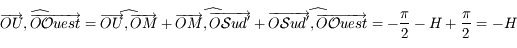 .
.
On a 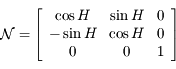 .
.
-
Question 3
Solution :
Par définition on a 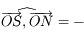 . Les points
. Les points  et
et 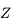 sont coplanaires, ainsi
sont coplanaires, ainsi 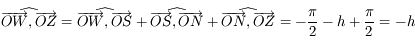 .
.
On a 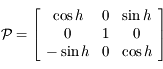 .
.
-
Question 4
Solution :
Par définition 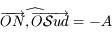 . Comme
. Comme 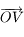 est orthogonal à
est orthogonal à 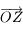 , on en déduit que
, on en déduit que 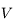 se trouve sur l'horizon céleste (par définition de
se trouve sur l'horizon céleste (par définition de 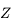 ). Ainsi, les points
). Ainsi, les points 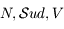 et
et 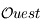 sont sur l'horizon céleste. On a donc:
sont sur l'horizon céleste. On a donc: 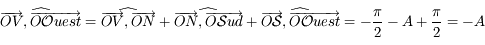 .
.
On a 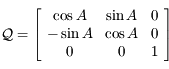 .
.
-
Question 5
Solution :
Les points 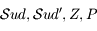 et
et 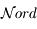 sont coplanaires. Ainsi
sont coplanaires. Ainsi 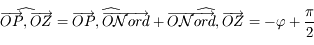 et
et 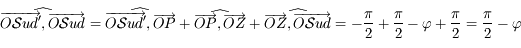 .
.
Avec 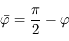 ,
on a
,
on a 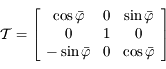 .
.
-
Question 6
Solution :
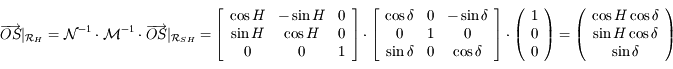 .
.
-
Question 7
Solution :
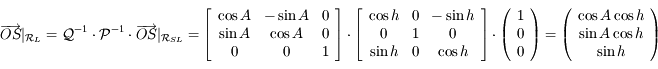 .
.
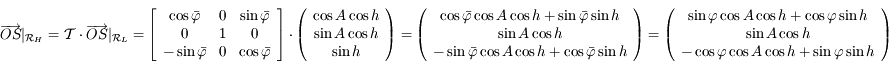 .
.
Ainsi on a 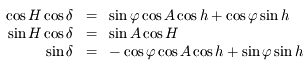 .
.
-
Question 8
Solution :
Au moment du coucher et du lever 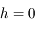 . Ainsi les trois relations deviennent:
. Ainsi les trois relations deviennent:
Ainsi on a 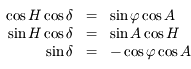 .
.
Sous réserve de la non annulation des dénominateurs, on peut diviser la première relation par la troisième pour obtenir : 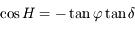 .
.
Ainsi on a 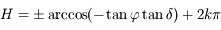 avec
avec 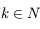 .
.
-
Question 9
Solution :
Pour  on a
on a 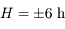 et la durée du jour est de 12h. On remarque que ce résultat est indépendant de
et la durée du jour est de 12h. On remarque que ce résultat est indépendant de 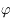 .
Pour
.
Pour 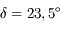 , on a
, on a 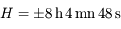 , donc la durée du jour est de
, donc la durée du jour est de 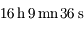 .
Pour
.
Pour 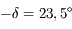 , on a
, on a 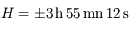 , donc la durée du jour est de
, donc la durée du jour est de 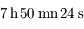 .
.
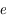 ) et la direction du péricentre (
) et la direction du péricentre (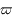 ), sont quasi constants. Plus précisément, soit ils varient peu (oscillations rapides de faible amplitude), soit ils varient lentement ("variations séculaires"). On dit que l'influence de Jupiter sur le mouvement de Saturne est une perturbation (et vice versa) du mouvement képlérien. L'objet de la mécanique céleste dans le cas de systèmes perturbés, est de modéliser ces variations.
), sont quasi constants. Plus précisément, soit ils varient peu (oscillations rapides de faible amplitude), soit ils varient lentement ("variations séculaires"). On dit que l'influence de Jupiter sur le mouvement de Saturne est une perturbation (et vice versa) du mouvement képlérien. L'objet de la mécanique céleste dans le cas de systèmes perturbés, est de modéliser ces variations.
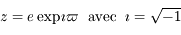
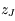 asssociée à Jupiter a le mouvement suivant:
asssociée à Jupiter a le mouvement suivant:

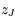 ) qui montre que l'exentricité de Jupiter est bornée.
) qui montre que l'exentricité de Jupiter est bornée.
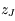 (Jupiter) et à
(Jupiter) et à 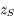 (Saturne) peut s'écrire:
(Saturne) peut s'écrire:
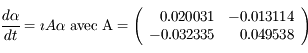
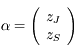
 est diagonalisable et donner ses valeurs propres (appelées ici, "fréquences propres").
est diagonalisable et donner ses valeurs propres (appelées ici, "fréquences propres").
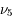 et
et 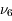 . Ces indices 5 et 6 font référence respectivement à la cinquième et à la sixième ligne de la matrice obtenue par Le Verrier lorsque celui-ci considérait les 8 planètes.
. Ces indices 5 et 6 font référence respectivement à la cinquième et à la sixième ligne de la matrice obtenue par Le Verrier lorsque celui-ci considérait les 8 planètes.
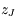 et
et 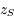 une solution sous la forme de termes périodiques. On montrera que les valeurs propres de la matrice
une solution sous la forme de termes périodiques. On montrera que les valeurs propres de la matrice 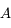 sont les fréquences de ces termes périodiques.
sont les fréquences de ces termes périodiques.
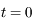 , on a les valeurs:
, on a les valeurs:
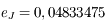 et
et 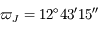
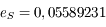 et
et 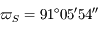
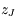 et
et 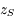 (on ne demande pas les phases)
(on ne demande pas les phases)
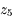 qui est représentée.
qui est représentée.

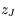 ) issue d'un système séculaire complet (non linéarisé et avec les 8 planètes).
) issue d'un système séculaire complet (non linéarisé et avec les 8 planètes).
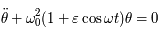
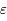 est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas,
est nul, c'est l'équation d'un pendule simple pour de petites oscillations. Dans ce cas, 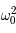 est inversement proportionnel à la longueur du pendule. On rappelle que la période
est inversement proportionnel à la longueur du pendule. On rappelle que la période 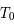 est alors
est alors 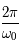 .
.
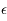 est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
est un petit paramètre. On dit que le modèle du pendule simple est perturbé. L'équation de Mathieu est un cas particulier de l'équation
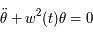
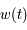 est une fonction périodique de période
est une fonction périodique de période 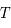 qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
qui est utilisée en Mécanique Céleste pour l'étude du mouvement de la Lune.
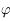 . Le point
. Le point 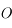 correspond à l'observateur. Il observe le mouvement du Soleil au cours d'une journée. Ce mouvement correspond uniquement à un changement de direction dans laquelle le Soleil est observé. Ainsi on peut représenter ce mouvement par un point se déplaçant sur une sphère (
correspond à l'observateur. Il observe le mouvement du Soleil au cours d'une journée. Ce mouvement correspond uniquement à un changement de direction dans laquelle le Soleil est observé. Ainsi on peut représenter ce mouvement par un point se déplaçant sur une sphère ( est de rayon qu'on prendra arbitrairement égale à 1.
est de rayon qu'on prendra arbitrairement égale à 1.
 .
Sur l'horizon céleste on peut représenter les directions du Sud
.
Sur l'horizon céleste on peut représenter les directions du Sud  , de l'Ouest
, de l'Ouest  , du Nord
, du Nord 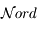 et de l'Est
et de l'Est 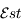 .
De même, on peut représenter la direction perpendiculaire à l'horizon: le Zénith (
.
De même, on peut représenter la direction perpendiculaire à l'horizon: le Zénith (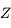 ) et la direction parallèle à l'axe de rotation de la Terre: le pôle céleste Nord (
) et la direction parallèle à l'axe de rotation de la Terre: le pôle céleste Nord (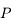 ). Le plan qui coupe la sphère céleste perpendiculaire à la direction
). Le plan qui coupe la sphère céleste perpendiculaire à la direction 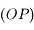 et passant par
et passant par 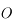 , s'appelle l'équateur céleste. Sur l'équateur céleste on note
, s'appelle l'équateur céleste. Sur l'équateur céleste on note 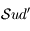 la direction du Sud. On note
la direction du Sud. On note 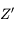 le Nadir, qui correspond à la direction opposée au Zénith, et on note
le Nadir, qui correspond à la direction opposée au Zénith, et on note 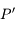 le pôle céleste Sud qui correspond à la direction opposée au pôle céleste nord. On remarquera que les points
le pôle céleste Sud qui correspond à la direction opposée au pôle céleste nord. On remarquera que les points 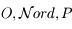 et
et 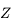 sont coplanaires avec
sont coplanaires avec 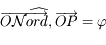 .
.
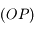 . Pour l'observateur, ceci ce traduit par un déplacement des astres observés sur des cercles parallèles à l'équateur céleste.
. Pour l'observateur, ceci ce traduit par un déplacement des astres observés sur des cercles parallèles à l'équateur céleste.
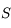 le point de la sphère céleste indiquant la direction dans laquelle est observé le Soleil depuis
le point de la sphère céleste indiquant la direction dans laquelle est observé le Soleil depuis 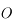 . On appelle
. On appelle 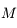 l'intersection de l'arc de
l'intersection de l'arc de 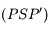 avec l'équateur céleste et
avec l'équateur céleste et 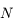 l'intersection de l'arc de grand cercle
l'intersection de l'arc de grand cercle 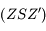 avec l'horizon céleste.
avec l'horizon céleste.
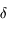 l'angle
l'angle 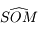 ,
, 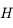 l'angle
l'angle 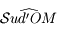 ,
, 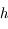 l'angle
l'angle 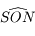 et
et 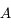 l'angle
l'angle 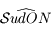 .
. 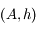 sont appelées les coordonnées locales, alors que
sont appelées les coordonnées locales, alors que 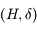 sont les coordonnées horaires. Au court du mouvement diurne d'une étoile seule
sont les coordonnées horaires. Au court du mouvement diurne d'une étoile seule 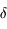 est constant. Pour le Soleil
est constant. Pour le Soleil 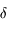 varie au cours de l'année, mais on peut le considérer constant sur une journée. L'animation permet de modifier
varie au cours de l'année, mais on peut le considérer constant sur une journée. L'animation permet de modifier 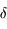 afin de voir les variations dans le mouvement diurne en fonction de
afin de voir les variations dans le mouvement diurne en fonction de 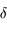 .
.

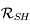 le repère
le repère 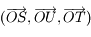 , où
, où 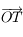 est perpendiculaire à
est perpendiculaire à 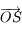 dans le plan
dans le plan 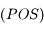 et tel que l'angle
et tel que l'angle 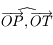 soit inférieur à
soit inférieur à 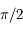 en valeur absolue et
en valeur absolue et 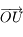 complète un repère orthonormé direct.
complète un repère orthonormé direct.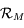 le repère
le repère 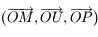 ,
, 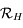 le repère
le repère 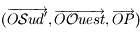 ,
,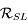 le repère
le repère 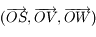 , où
, où 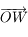 est perpendiculaire à
est perpendiculaire à 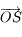 dans le plan
dans le plan 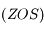 et tel que l'angle
et tel que l'angle 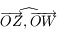 soit inférieur à
soit inférieur à 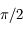 en valeur absolue et
en valeur absolue et 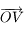 complète un repère orthonormé direct.
complète un repère orthonormé direct.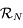 le repère
le repère 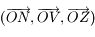 ,
,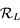 le repère
le repère 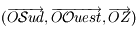 .
.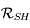 au repère
au repère 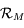 par une rotation d'angle
par une rotation d'angle 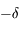 et d'axe
et d'axe 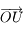 . Donner la matrice de passage
. Donner la matrice de passage 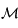 de la base de
de la base de 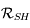 à celle de
à celle de 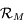 .
.
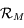 au repère
au repère 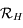 par une rotation d'angle
par une rotation d'angle 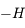 et d'axe
et d'axe 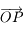 . Donner la matrice de passage
. Donner la matrice de passage 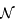 de la base de
de la base de 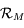 à celle de
à celle de 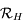 .
.
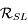 au repère
au repère 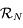 par une rotation d'angle
par une rotation d'angle 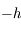 et d'axe
et d'axe 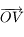 . Donner la matrice de passage
. Donner la matrice de passage 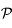 de la base de
de la base de 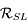 à celle de
à celle de 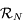 .
.
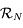 au repère
au repère 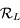 par une rotation d'angle
par une rotation d'angle 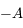 et d'axe
et d'axe 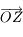 . Donner la matrice de passage
. Donner la matrice de passage  de la base de
de la base de 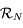 à celle de
à celle de 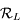 .
.
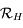 au repère
au repère 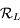 par une rotation d'angle
par une rotation d'angle 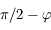 et d'axe
et d'axe 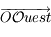 . Donner la matrice de passage
. Donner la matrice de passage 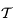 de la base de
de la base de 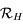 à celle de
à celle de 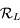 .
.
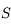 en fonction de
en fonction de  et
et 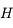 dans
dans 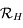 .
.
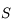 en fonction de
en fonction de 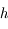 et
et 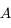 dans
dans 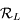 . Puis les coordonnées de
. Puis les coordonnées de 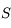 dans le repère
dans le repère 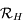 en fonction
de
en fonction
de 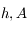 et
et 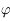 . En déduire trois relations, dépendant de
. En déduire trois relations, dépendant de 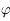 , entre les coordonnées horaires et les coordonnées locales du Soleil.
, entre les coordonnées horaires et les coordonnées locales du Soleil.
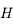 au moment du lever et du coucher du Soleil en fonction de
au moment du lever et du coucher du Soleil en fonction de 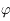 et
et 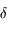 .
.
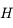 (mesuré entre -12h et +12h) et de la durée du jour au moment des équinoxes (
(mesuré entre -12h et +12h) et de la durée du jour au moment des équinoxes (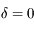 ), du solstice d'été
), du solstice d'été 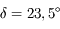 et du solstice d'hiver (
et du solstice d'hiver (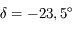 ) en un point de latitude
) en un point de latitude 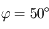 (approximativement la ville de Lille, France)
(approximativement la ville de Lille, France)
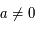 (entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
(entre autre). En déduire une équation de l'ellipse contenant cinq paramètres.
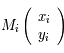 ,
, 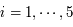 , ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
, ces 5 observations. Ecrire sous forme matricielle le système à résoudre.
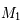 et
et 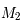 sont les plus simples possibles.
sont les plus simples possibles.
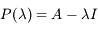 où
où  est la matrice identtée. Il est de degré 2. La résolution de
est la matrice identtée. Il est de degré 2. La résolution de 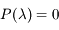 donnent les racines
donnent les racines 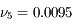 ''/jour et
''/jour et 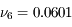 ''/jour. Ces valeurs propres sont distinctes donc
''/jour. Ces valeurs propres sont distinctes donc 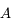 est diagonalisable.
est diagonalisable.
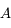 est diagonalisable donc il existe une matrice
est diagonalisable donc il existe une matrice 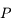 tel que:
tel que:
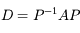 avec
avec 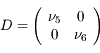
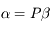
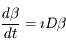
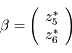 , le système est trivialement intégrable:
, le système est trivialement intégrable:
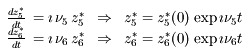
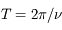 ou plutôt
ou plutôt 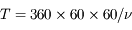 puisque
puisque 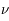 est donné en seconde de degré (par jour). Il faut encore diviser le résultat par
est donné en seconde de degré (par jour). Il faut encore diviser le résultat par 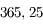 pour l'avoir en année.
pour l'avoir en année.
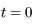 , il faudra inverser un système
, il faudra inverser un système 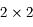 .
.
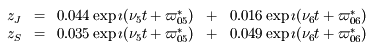
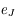 varie entre
varie entre 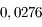 et
et 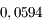
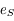 varie entre
varie entre 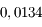 et
et 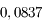
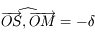 . Les points
. Les points 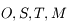 et
et 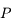 sont coplanaires, ainsi
sont coplanaires, ainsi 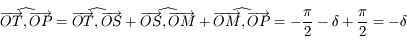 .
.
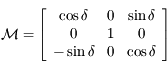 .
.
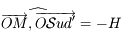 . Comme
. Comme 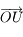 est orthogonal à
est orthogonal à 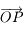 , on en déduit que
, on en déduit que 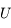 se trouve sur l'équateur céleste (par définition de l'équateur céleste). De même,
se trouve sur l'équateur céleste (par définition de l'équateur céleste). De même, 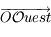 est perpendiculaire au plan
est perpendiculaire au plan 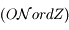 qui est confondu avec le plan
qui est confondu avec le plan 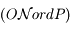 . Ainsi
. Ainsi 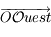 est orthogonal à
est orthogonal à 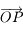 , donc le point
, donc le point  se trouve aussi sur l'équateur céleste. Finalement, les points
se trouve aussi sur l'équateur céleste. Finalement, les points  et
et 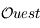 sont sur l'équateur céleste. On a donc:
sont sur l'équateur céleste. On a donc: 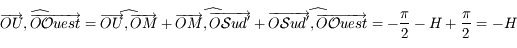 .
.
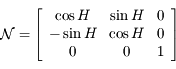 .
.
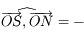 . Les points
. Les points  et
et 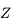 sont coplanaires, ainsi
sont coplanaires, ainsi 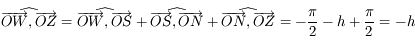 .
.
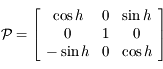 .
.
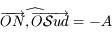 . Comme
. Comme 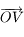 est orthogonal à
est orthogonal à 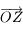 , on en déduit que
, on en déduit que 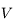 se trouve sur l'horizon céleste (par définition de
se trouve sur l'horizon céleste (par définition de 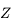 ). Ainsi, les points
). Ainsi, les points 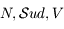 et
et 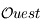 sont sur l'horizon céleste. On a donc:
sont sur l'horizon céleste. On a donc: 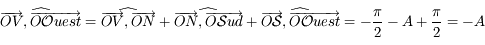 .
.
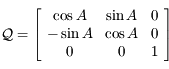 .
.
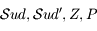 et
et 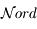 sont coplanaires. Ainsi
sont coplanaires. Ainsi 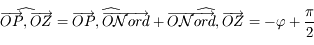 et
et 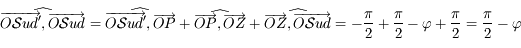 .
.
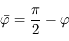 ,
on a
,
on a 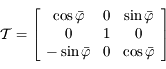 .
.
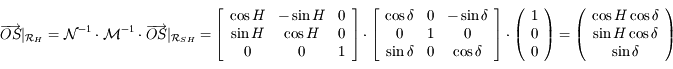 .
.
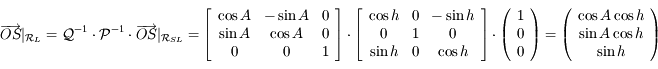 .
.
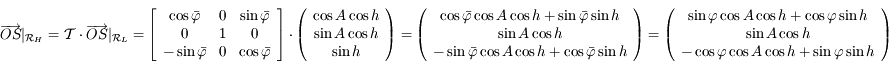 .
.
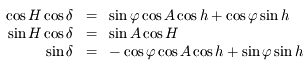 .
.
 . Ainsi les trois relations deviennent:
. Ainsi les trois relations deviennent:
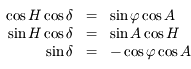 .
.
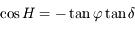 .
.
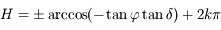 avec
avec  .
.
 on a
on a 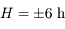 et la durée du jour est de 12h. On remarque que ce résultat est indépendant de
et la durée du jour est de 12h. On remarque que ce résultat est indépendant de 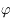 .
Pour
.
Pour 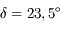 , on a
, on a 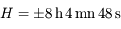 , donc la durée du jour est de
, donc la durée du jour est de 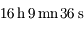 .
Pour
.
Pour 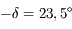 , on a
, on a 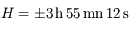 , donc la durée du jour est de
, donc la durée du jour est de 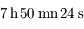 .
.
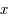 et
et 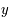 de degré deux, c'est-à-dire :
de degré deux, c'est-à-dire :
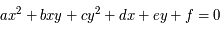 ,
,
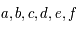 sont des constantes réelles.
sont des constantes réelles.
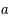 . On obtient :
. On obtient :
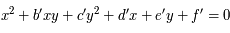 .
.
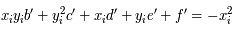 .
.
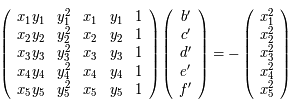 .
.
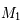 à l'origine et
à l'origine et 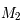 qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a
qui nous définie l'axe des abscisses ainsi que la norme. Ainsi on a 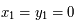 , et
, et 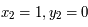 .
.
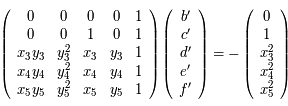 .
.
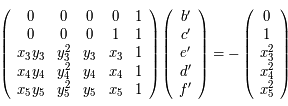 .
.
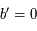 et
et 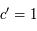 .
.
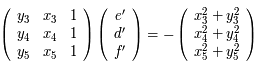 .
.