Auteur: Alain Vienne
La loi des aires dit que, dans le problème de l'interaction gravitationnelle de deux corps, l'aire balayée par le rayon vecteur est proportionnel au temps. Cette loi est aussi appelée "deuxième loi de Kepler" (voir aussi dans ce même chapitre, le lien suivant).
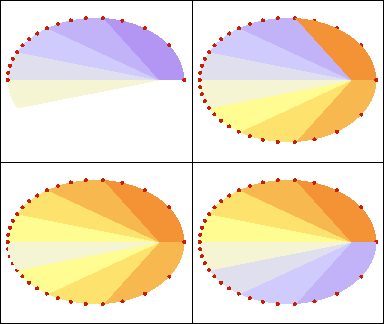
La loi des aires : les aires décrites par le mobile dans des temps égaux sont égales.
Ainsi, lorsque l'astre s'éloigne du Soleil, sa vitesse diminue.
En fait, la loi des aires est plus générale que la deuxième loi de Kepler puisque qu'elle s'applique pour toute force centrale. Pour la démontrer, il faut bien-sur utiliser la loi fondamentale de la dynamique:
Principe fondamental de la dynamique
L'accélération d'un mobile est proportionnelle à la force à laquelle il est soumis.
La preuve qui est proposée en exercice utilise un modèle discret. Elle est directement inspirée d'une application isssue du livre de Daniel Perrin "Nombre, mesures et géométrie" (Ed. CASSINI). Ainsi le temps est une juxtaposition d'instants 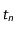 de durée très courte
de durée très courte 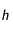 de telle sorte que
de telle sorte que 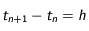 . La discrétisation revient à supposer qu'entre les instants
. La discrétisation revient à supposer qu'entre les instants 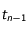 et
et 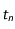 , le mobile se déplace de
, le mobile se déplace de 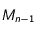 à
à 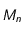 avec la vistesse constante
avec la vistesse constante 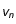 . En vecteur la vistesse est donc
. En vecteur la vistesse est donc 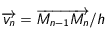 . Sur l'intervalle suivant
. Sur l'intervalle suivant ![[t_n,t_{n+1}]](../pages_applications/equations_applications/equation10.png) , la vitesse est différente mais constante aussi pour cette durée:
, la vitesse est différente mais constante aussi pour cette durée: 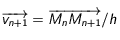 . Ainsi à l'instant
. Ainsi à l'instant 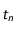 l'accélération est
l'accélération est 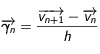 .
.
Le modèle continu s'obtient facilement par passage à la limite.
La loi fondamentale de la dynamique s'écrit alors: 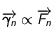
Les outils mathématiques nécéssaires à cette preuve se limitent alors à deux petits lemmes que Daniel Perrin nomment lemmes de découpage et que nous admettrons:
Auteur: Alain Vienne
 La loi des aires
La loi des aires
Difficulté : ☆☆
Temps : 1h
Question 1)
Montrer qu'à tout instant (c'est-à-dire pour tout entier 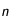 ), on a:
), on a: 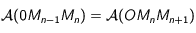
Cela signifie bien que l'aire balayé par le rayon vecteur 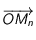 est proportionnel au temps parcouru.
est proportionnel au temps parcouru.
Lemme de la médiane dans le triangle 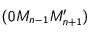 pour avoir
pour avoir 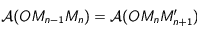
Auteur: S. Renner
Date de création: 2 mars 2009
 Introduction
Introduction
L'effet Doppler-Fizeau représente le décalage en fréquence d'une onde lumineuse entre les mesures à l'émission et à la réception, lorsque la distance entre un émetteur et un récepteur varie au cours du temps.
Par exemple, lors du passage d'un camion de pompier muni d'une sirène, c'est l'effet Doppler qui se manifeste dans la perception de la hauteur du son (plus aigu lorsque le véhicule se rapproche, plus grave lorsqu'il s'éloigne).
Ce phénomène est particulièrement important en astronomie car il permet de mesurer les vitesses (d'approche ou d'éloignement) des objets célestes.
On observe Arcturus, troisième étoile la plus brillante du ciel (dans la constellation du Bouvier), à deux dates 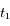 et
et 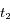 espacées de 6 mois.
espacées de 6 mois.
La latitude par rapport au plan de l'orbite de la Terre est 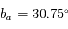 , et la longitude par rapport à une direction fixe
, et la longitude par rapport à une direction fixe 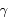 est
est 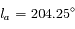 . A l'instant
. A l'instant 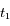 la longitude de la Terre est
la longitude de la Terre est 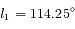 , et
, et 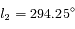 à l'instant
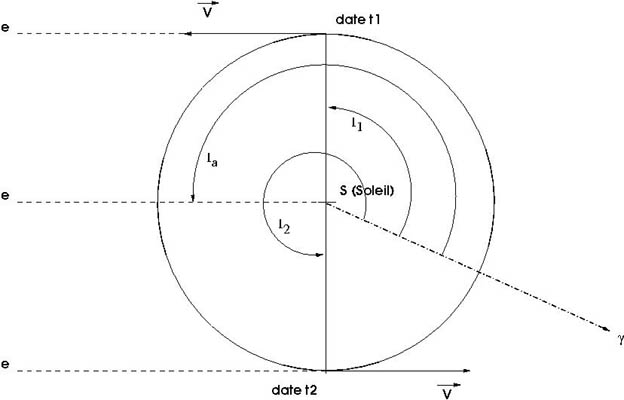
à l'instant 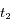 . Voir la figure ci-dessous pour les conditions d'observation.
. Voir la figure ci-dessous pour les conditions d'observation.
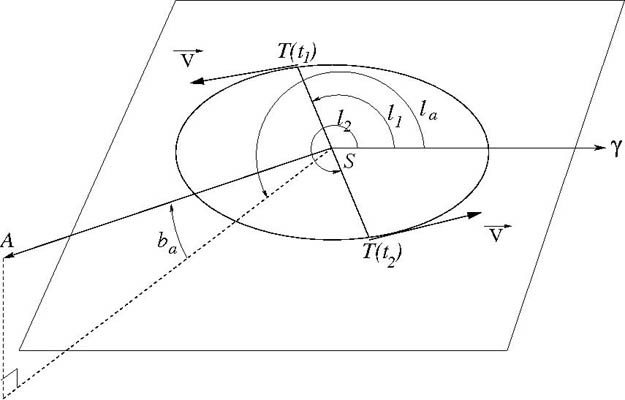
Situation de l'observation d'Arcturus. Voir texte pour la valeur des angles.
On effectue aux dates 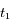 et
et 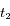 un spectre de la lumière de l'étoile. L'étude des raies d'absorption permet de remarquer qu'une raie d'absorption du fer, qui normalement se situe à
un spectre de la lumière de l'étoile. L'étude des raies d'absorption permet de remarquer qu'une raie d'absorption du fer, qui normalement se situe à 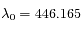 nm, est mesurée
nm, est mesurée 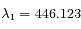 nm sur le spectre obtenu à la date
nm sur le spectre obtenu à la date 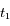 , et
, et 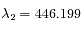 nm sur celui obtenu à la date
nm sur celui obtenu à la date 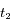 .
.
L'objectif est d'en déduire la vitesse orbitale de la Terre autour du Soleil, ainsi que la distance moyenne Terre-Soleil.
Auteur: S. Renner
 Vitesse orbitale de la Terre
Vitesse orbitale de la Terre
Difficulté : ☆
Temps : 1h30
On fait l'hypothèse que l'orbite de la Terre est circulaire est que celle-ci est décrite avec une vitesse uniforme 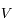 .
.
Question 4)
Calculer la distance Terre-Soleil en km sachant que la période de révolution est 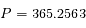 jours.
jours.
Auteur: S. Renner
Date de création: 16 mai 2013
On reprend les résultats obtenus dans l'exercice sur la résolution du problème des 2 corps. Le but ici est d'établir l'équation de Kepler à l'aide de la géométrie essentiellement, plutôt que par le calcul.
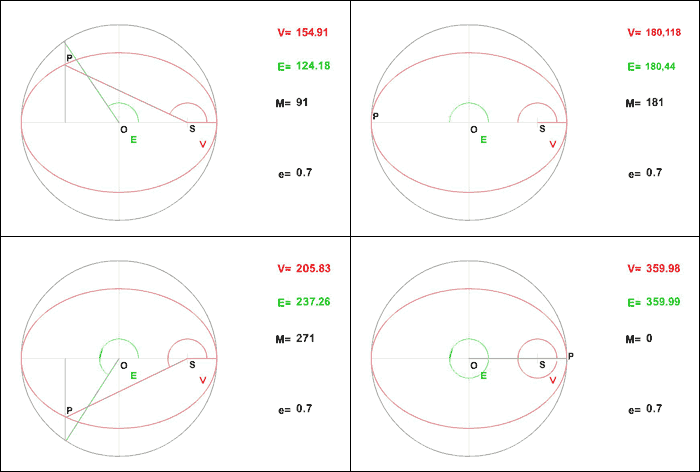
L'équation de Kepler (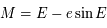 ) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne
) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne 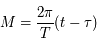 , avec
, avec 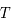 la période orbitale,
la période orbitale,  le temps et
le temps et 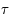 l'instant de passage au péricentre.
l'instant de passage au péricentre.
Les trois anomalies
Auteur: S. Renner
 Equation de Kepler
Equation de Kepler
Difficulté : ☆
Temps : 1h
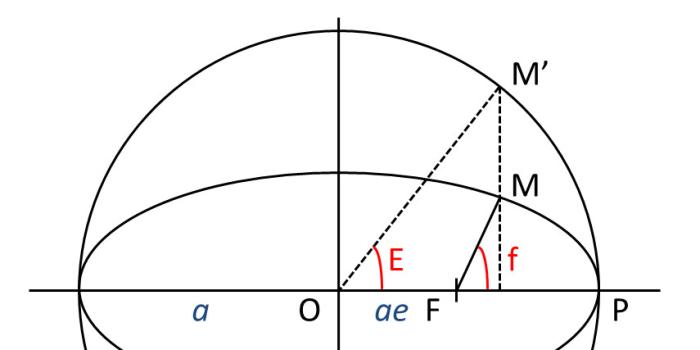
Trajectoire elliptique d'un corps
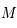
(de foyer
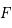
, péricentre
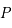
, demi-grand axe
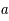
, excentricité
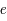
), cercle principal, anomalie excentrique
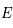
et vraie
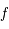
Question 2)
Calculer l'aire délimitée par les points 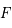 ,
, 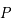 ,
, 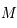 .
.
Question 3)
En déduire l'équation de Kepler 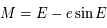 .
.

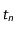 de durée très courte
de durée très courte 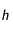 de telle sorte que
de telle sorte que 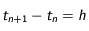 . La discrétisation revient à supposer qu'entre les instants
. La discrétisation revient à supposer qu'entre les instants 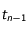 et
et 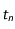 , le mobile se déplace de
, le mobile se déplace de 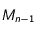 à
à 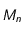 avec la vistesse constante
avec la vistesse constante 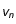 . En vecteur la vistesse est donc
. En vecteur la vistesse est donc 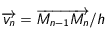 . Sur l'intervalle suivant
. Sur l'intervalle suivant ![[t_n,t_{n+1}]](../pages_applications/equations_applications/equation10.png) , la vitesse est différente mais constante aussi pour cette durée:
, la vitesse est différente mais constante aussi pour cette durée: 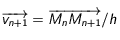 . Ainsi à l'instant
. Ainsi à l'instant 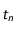 l'accélération est
l'accélération est 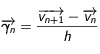 .
.
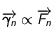
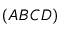 un parallélogramme. La diagonale
un parallélogramme. La diagonale ![[AC]](../pages_applications/equations_applications/equation16.png) partage le parallélogramme en deux triangles de même aire:
partage le parallélogramme en deux triangles de même aire: 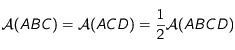 . Plus généralement, pout tout point
. Plus généralement, pout tout point 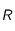 de
de ![[CD]](../pages_applications/equations_applications/equation19.png) , on a :
, on a : 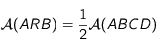 .
.
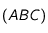 un triangle et
un triangle et 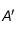 le milieu de
le milieu de ![[BC]](../pages_applications/equations_applications/equation23.png) . La médiane
. La médiane ![[AA']](../pages_applications/equations_applications/equation24.png) partage le triangle en deux triangles de même aire:
partage le triangle en deux triangles de même aire: 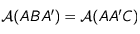 .
.
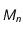 est soumis à une force centrale, c'est-à-dire dirigée vers un point
est soumis à une force centrale, c'est-à-dire dirigée vers un point 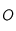 fixe (le Soleil par exemple si la masse de
fixe (le Soleil par exemple si la masse de 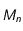 est négligeable par rapport à celle du Soleil): la force est
est négligeable par rapport à celle du Soleil): la force est 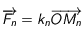 .
.
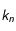 même si on sait que pour la loi de Newton ce scalaire est négatif et inversement proportionnel au carré de la distance
même si on sait que pour la loi de Newton ce scalaire est négatif et inversement proportionnel au carré de la distance 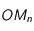
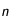 ), on a:
), on a: 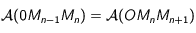
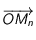 est proportionnel au temps parcouru.
est proportionnel au temps parcouru.
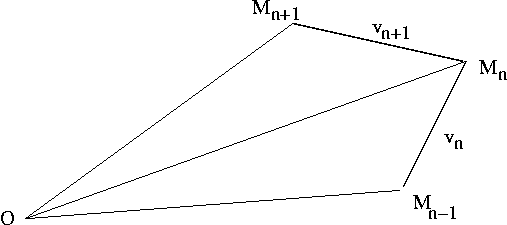
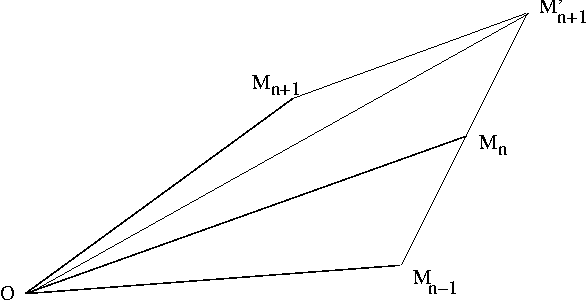
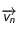 et
et 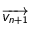 (vitesses du mobile aux temps
(vitesses du mobile aux temps 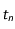 et
et 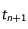 ) et considérer le point
) et considérer le point 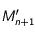 qu'occuperait le mobile au temps
qu'occuperait le mobile au temps 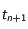 si le mouvement était uniforme.
si le mouvement était uniforme.
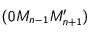 pour avoir
pour avoir 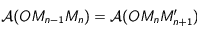
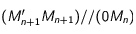 , puis prendre
, puis prendre 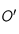 de telle manière que
de telle manière que 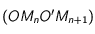 soit un parallélogramme et enfin lui appliquer le lemme correspondant avec
soit un parallélogramme et enfin lui appliquer le lemme correspondant avec 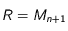 puis avec
puis avec 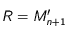 .
.
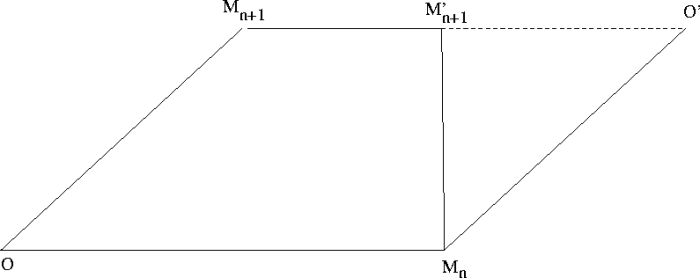
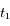 et
et 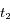 espacées de 6 mois.
espacées de 6 mois.
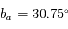 , et la longitude par rapport à une direction fixe
, et la longitude par rapport à une direction fixe 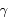 est
est 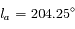 . A l'instant
. A l'instant 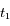 la longitude de la Terre est
la longitude de la Terre est 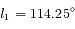 , et
, et 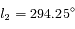 à l'instant
à l'instant 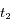 . Voir la figure ci-dessous pour les conditions d'observation.
. Voir la figure ci-dessous pour les conditions d'observation.

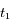 et
et 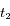 un
un 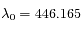 nm, est mesurée
nm, est mesurée 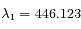 nm sur le spectre obtenu à la date
nm sur le spectre obtenu à la date 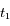 , et
, et 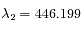 nm sur celui obtenu à la date
nm sur celui obtenu à la date 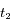 .
.
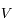 .
.
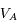 la
la 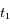 et
et 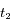 ). Ecrire en fonction de
). Ecrire en fonction de 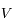 ,
, 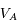 et
et 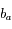 la vitesse radiale d'Arcturus par rapport à l'observateur à l'instant
la vitesse radiale d'Arcturus par rapport à l'observateur à l'instant 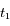 (on notera cette vitesse
(on notera cette vitesse 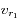 ), ainsi qu'à l'instant
), ainsi qu'à l'instant 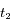 (notée
(notée 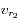 ).
).
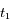 et
et 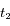 pour la longueur d'onde de référence
pour la longueur d'onde de référence 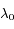 , écrire les expressions de
, écrire les expressions de 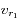 et
et 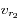 .
.
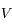 et
et 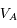 en fonction des longueurs d'onde
en fonction des longueurs d'onde 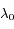 ,
, 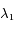 et
et 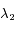 . Calculer leur valeur numériquement en km.s
. Calculer leur valeur numériquement en km.s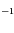 .
.
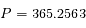 jours.
jours.
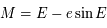 ) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne
) est importante car elle fait le lien entre la position de l'objet sur son orbite (voir la figure ci-dessous) et le temps, ou plus précisément l'anomalie moyenne 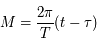 , avec
, avec 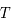 la période orbitale,
la période orbitale,  le temps et
le temps et 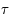 l'instant de passage au péricentre.
l'instant de passage au péricentre.


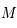 (de foyer
(de foyer 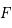 , péricentre
, péricentre 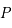 , demi-grand axe
, demi-grand axe 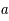 , excentricité
, excentricité 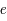 ), cercle principal, anomalie excentrique
), cercle principal, anomalie excentrique 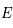 et vraie
et vraie 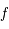
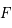 ,
, 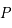 ,
, 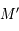 en fonction de
en fonction de 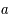 ,
, 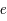 ,
, 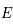 .
.
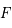 ,
, 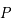 ,
, 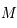 .
.
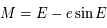 .
.
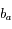 (angle entre la direction de l'étoile et le plan de l'écliptique).
(angle entre la direction de l'étoile et le plan de l'écliptique).
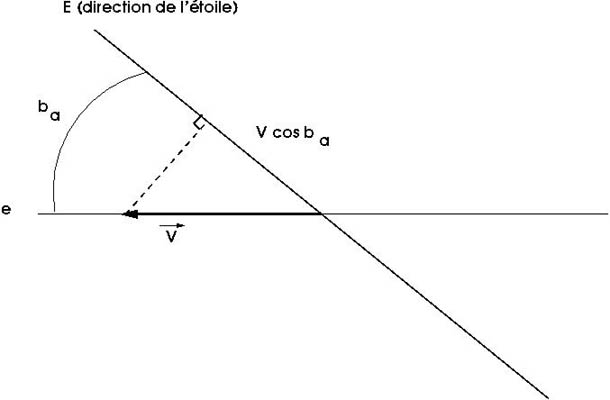
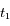 . Ainsi la vitesse radiale mesurée, due au seul mouvement de la Terre, a pour module
. Ainsi la vitesse radiale mesurée, due au seul mouvement de la Terre, a pour module 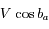 .
.
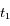 ,
, 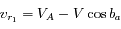
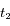 ,
, 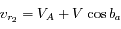
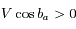
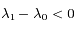 , donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant
, donc l'étoile et l'observateur se rapprochent (bleuissement des raies) à l'instant 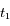 et
et 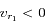
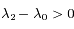 , donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant
, donc l'étoile et l'observateur s'éloignent (rougissement des raies) à l'instant 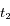 et
et 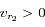
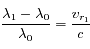
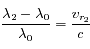
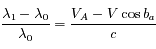 (1)
(1)
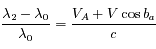 (2)
(2)
![\Longrightarrow V_A=\frac{c}{2 \lambda_0} [ (\lambda_1 - \lambda_0) + (\lambda_2 - \lambda_0) ]](../pages_applications/equations_applications/equation104.png)
![\Longrightarrow V=\frac{c}{2 \lambda_0 \cos b_a} [ (\lambda_2 - \lambda_0) - (\lambda_1 - \lambda_0) ]](../pages_applications/equations_applications/equation105.png)
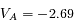 km.s
km.s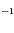
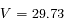 km.s
km.s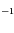
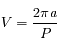
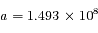 km.
km.
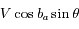 , où
, où 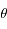 croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence
croît uniformément avec le temps. L'amplitude maximale de l'oscillation d'une raie autour de la valeur de référence 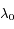 sera
sera 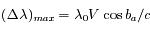 . Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer
. Dans l'exercice, les conditions d'observation correspondent à cette amplitude maximale (obtenue lorsque les directions Soleil-Terre et Soleil-étoile sont perpendiculaires). Ainsi la mesure du décalage maximum permet, pour une étoile de direction connue, de déterminer 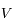 .
.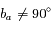 ). L'effet de décalage est d'autant plus important que
). L'effet de décalage est d'autant plus important que 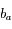 est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.
est petit, et il est maximal pour une étoile dont la direction se trouve dans le plan de l'écliptique.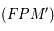 = aire
= aire 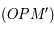 - aire
- aire 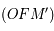
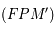 =
= 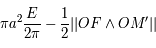
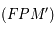 =
= 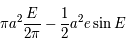
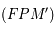 =
= 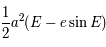
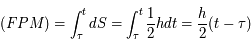
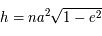 , où
, où 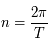 est le moyen mouvement.
est le moyen mouvement.
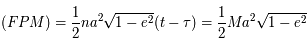 .
.
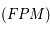 =
=  aire
aire 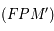 =
= 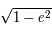 aire
aire 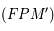 , où
, où 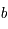 est le demi-petit axe de l'ellipse.
est le demi-petit axe de l'ellipse.
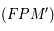 =
= 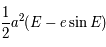 et aire
et aire 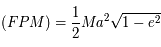 . On obtient donc
. On obtient donc 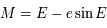 .
.