Auteur: S. Renner
 Orbite de Mars
Orbite de Mars
Difficulté : ☆
Temps : 2h30
Question 1)
L'observation de Mars en opposition a fourni la période qui sépare ces oppositions, ou période synodique notée 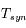 . Cette période est égale à 780 jours.
. Cette période est égale à 780 jours.
En déduire la valeur de la période sidérale de mars, que l'on notera 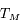 .
.
Question 2)
Calculer la durée qui sépare les 2 dates successives de chaque couple d'observations. Quelle conclusion peut-on en tirer?
Question 3)
Trouver la relation entre la longitude écliptique héliocentrique de la Terre 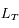 (angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil
(angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil 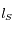 . Calculer
. Calculer 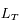 pour chacune des dates du tableau.
pour chacune des dates du tableau.
Question 4)
Représenter sur une feuille de papier millimétré l'orbite de la Terre par un cercle de centre 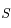 (Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
(Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
Pour chacun des 5 couples d'observations, construire:
- la première position Ti de la Terre sur son orbite et la direction Tix de Mars telle qu'on l'observe depuis la Terre
- la seconde position T'i de la Terre sur son orbite et la direction T'ix' de Mars
Montrer que le point Mi représentant Mars est à l'intersection des deux demi-droites Tix et T'ix'.
On déterminera ainsi les 5 positions de M1, M2, M3, M4 et M5 de Mars.
Question 5)
Vérifier que ces 5 points ne sont pas sur un cercle centré sur le Soleil.
Dans ce qui suit, on admet que l'orbite de Mars est une ellipse de faible excentricité, dont la forme ne diffère pas significativement de celle d'un cercle, mais dont le centre n'est pas le Soleil.
Pour déterminer le rayon de ce cercle, on partira d'une première approximation qui est la moyenne des 5 rayons SMi. On tracera le cercle ayant ce rayon sur une feuille de papier calque et on cherchera, par tâtonnement, à le faire passer au mieux parmi les 5 points Mi. Si le rayon du cercle est trop petit, la majorité des points se trouveront toujours à l'extérieur du cercle; inversement, s'il est trop grand, la majorité des points se trouveront toujours à l'intérieur. On modifiera donc le rayon de ce cercle, millimètre par millimètre, pour qu'il passe au mieux parmi les 5 points. Soit alors 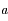 la valeur du rayon de ce cercle.
la valeur du rayon de ce cercle.
Autre possibilité: connaissant la période sidérale de Mars, calculer son demi-grand axe en UA (unité astronomique, égale à la distance moyenne Terre-Soleil, soit 149 597 871 km). Tracer le cercle correspondant à cette orbite et estimer une erreur en mm sur les positions de Mars.
Question 7)
Sachant que l'excentricité de la Terre est 0.016, l'approximation de l'orbite de la Terre par un cercle centré sur le Soleil est-elle justifiée?
Question 8)
Quelle est la distance minimale de Mars à la Terre lors d'une opposition? A quelle date de l'année ces oppositions favorables se produisent-elles? Quelle est la distance maximale de Mars à la Terre lors d'une opposition? A quelle date de l'année ces oppositions défavorables se produisent-elles?
Question 9)
Afin de vérifier la loi des aires, mesurer l'aire balayée par le rayon-vecteur Soleil-Mars entre le 6 août et le 7 décembre 1593 et celle balayée entre le 26 janvier et le 28 mars 1587. En déduire la valeur moyenne de l'aire balayée par jour dans chacun des deux cas. On pourra, pour cela, compter les carreaux du papier.
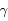 ).
La tableau ci-dessous rassemble les données concernant 5 couples d'observations de Mars, effectuées par Tycho Brahé. On y indique la longitude écliptique géocentrique du Soleil, notée
).
La tableau ci-dessous rassemble les données concernant 5 couples d'observations de Mars, effectuées par Tycho Brahé. On y indique la longitude écliptique géocentrique du Soleil, notée 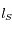 (c'est-à-dire l'angle, mesurée depuis la Terre, entre la direction du Soleil et celle du point vernal), et la longitude écliptique géocentrique de Mars, notée
(c'est-à-dire l'angle, mesurée depuis la Terre, entre la direction du Soleil et celle du point vernal), et la longitude écliptique géocentrique de Mars, notée 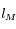 (angle vu de la Terre entre la direction de Mars et celle du point vernal).
(angle vu de la Terre entre la direction de Mars et celle du point vernal).
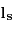
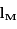
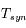 . Cette période est égale à 780 jours.
. Cette période est égale à 780 jours.
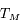 .
.
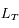 (angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil
(angle entre la direction de la Terre et celle du point vernal mesurée depuis le Soleil) et la longitude géocentrique du Soleil 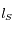 . Calculer
. Calculer 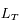 pour chacune des dates du tableau.
pour chacune des dates du tableau.
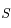 (Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
(Soleil) et de rayon égal à 5 cm. Choisir la direction du point vernal selon une des lignes du papier.
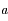 la valeur du rayon de ce cercle.
la valeur du rayon de ce cercle.
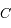 du cercle ainsi déterminé au point
du cercle ainsi déterminé au point 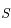 (Soleil). En déduire l'excentricité de l'orbite
(Soleil). En déduire l'excentricité de l'orbite 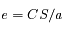 .
.
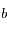 de l'ellipse, et discuter la validité de l'approximation faite ici, qui a conduit à assimiler l'ellipse à un cercle de rayon
de l'ellipse, et discuter la validité de l'approximation faite ici, qui a conduit à assimiler l'ellipse à un cercle de rayon 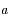 .
.
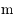 par rapport à un corps central de masse
par rapport à un corps central de masse 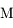 et de rayon
et de rayon 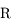 . On note
. On note 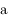 le demi-grand axe du satellite,
le demi-grand axe du satellite, 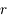 sa distance au corps central, et
sa distance au corps central, et 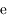 son excentricité supposée faible (
son excentricité supposée faible (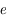 <<1).
<<1).
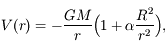 où
où 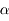 est une constante <<1 qui caractérise l'applatissement. On peut montrer qu'alors l'équation du mouvement du satellite s'écrit:
est une constante <<1 qui caractérise l'applatissement. On peut montrer qu'alors l'équation du mouvement du satellite s'écrit:
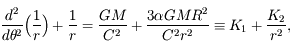 où
où 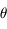 est la position angulaire du satellite sur sa trajectoire (
est la position angulaire du satellite sur sa trajectoire (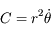 le moment cinétique.
le moment cinétique.
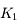 et
et 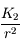 , et en déduire que la trajectoire du satellite est peu modifiée sous l'effet de l'applatissement du corps central, par rapport au problème à 2 corps classique.
, et en déduire que la trajectoire du satellite est peu modifiée sous l'effet de l'applatissement du corps central, par rapport au problème à 2 corps classique.
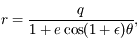 avec
avec 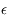 <<1, et exprimer
<<1, et exprimer 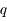 et
et 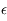 en fonction de
en fonction de 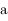 ,
, 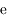 ,
, 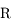 et
et 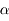 .
.
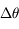 du périastre de la trajectoire, c'est-à-dire l'angle dont les axes de l'ellipse ont tourné après une révolution du satellite.
du périastre de la trajectoire, c'est-à-dire l'angle dont les axes de l'ellipse ont tourné après une révolution du satellite.
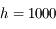 km autour de la Terre (
km autour de la Terre (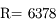 km,
km, 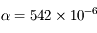 ).
).
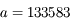 km et période orbitale
km et période orbitale 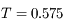 jours) autour de Saturne (
jours) autour de Saturne (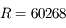 km,
km, 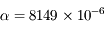 ).
).
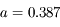 UA
UA 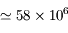 km,
km, 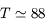 jours) autour du Soleil (
jours) autour du Soleil (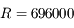 km,
km, 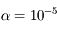 ). La précession observée du périhélie de Mercure s'élève en fait à
). La précession observée du périhélie de Mercure s'élève en fait à 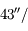 siècle. Commenter.
siècle. Commenter.
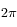 , c'est-à-dire:
, c'est-à-dire: 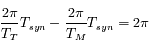 .
.
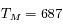 jours
jours
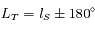 (modulo 360°).
(modulo 360°).
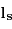
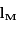
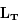
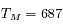 jours et
jours et 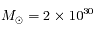 kg, on trouve
kg, on trouve 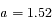 UA. Or 1 UA = 50 mm, donc le rayon du cercle est 76 mm.
UA. Or 1 UA = 50 mm, donc le rayon du cercle est 76 mm.
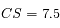 mm. Comme 1 UA = 50 mm, on en déduit que
mm. Comme 1 UA = 50 mm, on en déduit que 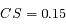 UA.
UA.
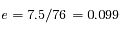 (à comparer à la valeur exacte: 0.093)
(à comparer à la valeur exacte: 0.093)
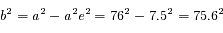 d'où
d'où 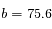 mm
mm 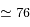 mm.
mm.
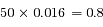 mm. Donc l'approximation est correcte étant donnée la précision du tracé.
mm. Donc l'approximation est correcte étant donnée la précision du tracé.
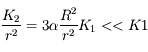 car
car 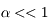 ,
, 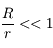
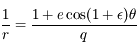
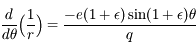
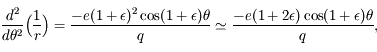 car
car 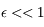 .
.
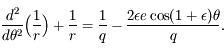
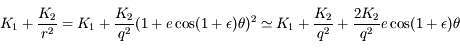 , car
, car 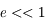 .
.
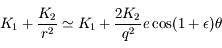 , car
, car 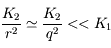 .
.
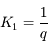 et
et 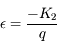 .
.
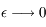 ,
, 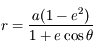 (solution du problème keplerien) donc
(solution du problème keplerien) donc 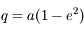 .
.
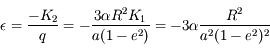 donc
donc 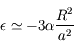 .
.
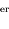 passage au périastre
passage au périastre 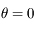 , au 2
, au 2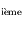 passage
passage  .
.
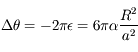 .
.
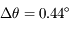
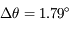
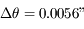 , i.e
, i.e 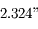 /siècle (période orbitale de Mercure = 88 jours). En fait la précession réelle est de
/siècle (période orbitale de Mercure = 88 jours). En fait la précession réelle est de 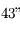 /siècle et s'explique par la relativité générale. Dans cette théorie,
/siècle et s'explique par la relativité générale. Dans cette théorie, 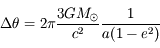 , où
, où 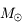 désigne la masse du Soleil.
désigne la masse du Soleil.