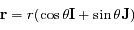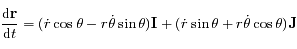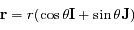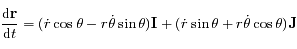On a vu que {\mathbf r}=r(\cos \theta {\mathbf I}+\sin \theta {\mathbf J}) et \frac{{\rm d}{\mathbf r}}{{\rm d}t}=(\dot{r} \cos \theta-r\dot{\theta} \sin \theta) {\mathbf I} + (\dot{r}\sin \theta+r\dot{\theta}\cos \theta) {\mathbf J}.

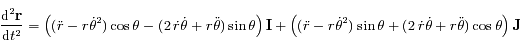Ainsi \frac{{\rm d}^2 {\mathbf r}}{{\rm d}t^2}=\left( (\ddot{r}-r\dot{\theta}^2)\cos \theta -(2\, \dot{r}\dot{\theta}+r\ddot{\theta})\sin \theta \right) {\mathbf I} + \left( (\ddot r} -r\dot{\theta}^2)\sin \theta + (2\, \dot{r}\dot{\theta}+r\ddot{\theta})\cos \theta \right ) {\mathbf J}.

L'équation du mouvement est équivalente au système:

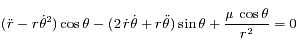
(\ddot{r}-r\dot{\theta}^2)\cos \theta - (2\,\dot{r}\dot{\theta}+r\ddot{\theta})\sin \theta + \frac{\mu\, \cos \theta}{r^2} =0

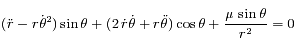
(\ddot{r}-r\dot{\theta}^2)\sin \theta + (2\,\dot{r}\dot{\theta}+r\ddot{\theta})\cos \theta + \frac{\mu\, \sin \theta}{r^2} =0

En mutlipliant la première équation par 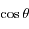\cos \theta et la deuxième par 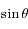\sin \theta et en sommant les deux équations obtenues d'une part ; et en multipliant la première équation par 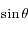\sin \theta et la deuxième par 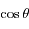\cos \theta et en soustrayant les deux équations obtenues d'autre part ; on obtient le système suivant:

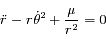
\ddot{r}-r\dot{\theta}^2+\frac{\mu}{r^2}=0

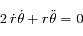
2\,\dot{r}{\dot{\theta}+r\ddot{\theta}=0

On montre facilement que la deuxième équation correspond bien à 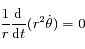\frac{1}{r}\frac{{\rm d}}{{\rm d}t} (r^2 \dot{\theta}) = 0.