Auteur: Marc Fouchard
 Loi de Wien
Loi de Wien
Difficulté : ☆☆
Temps : 2h
Question 3)
En déduire qu'il doit exister un maximum pour 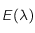 sur
sur 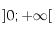 .
.
Auteur : Jérôme Thiébaut
Une étoile à neutron constitue l'étape ultime d'évolution des étoiles de masses inférieures à trois masses solaires. Ayant brulé tout son carburant, l'étoile devient une supernova, elle éjecte ses couches extérieures et son coeur s'éffondre sur lui même. Les électrons et les protons fusionnent ensemble et se transforment en neutrons. La densité devient alors comparable à celle de la matière nucléaire et la température est de l'ordre de 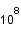 K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
Auteur: Jérôme Thiébaut
 Etoile à neutron
Etoile à neutron
Difficulté : ☆
Temps : 45 min
On assimile l'étoile à neutron à un gaz parfait de neutrons contenu dans une sphère. La densité d'états (ou fonction de distribution) de l'impulsion 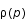 est la suivante:
est la suivante: 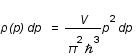 , où V est le volume et
, où V est le volume et 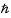 la constante de Planck réduite.
la constante de Planck réduite.
Question 1)
On définit la densité de particule n:
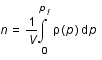 où
où 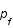 est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de
est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de 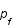 .
.
Question 2)
Exprimer l'impulsion de Fermi en fonction de la masse du neutron, m, celle de l'étoile, M, et du rayon de l'étoile, R.
Calculer d'abord la densité de particules en fonction des caractéristiques de l'étoile.
Question 4)
L'énergie du gaz E vallant 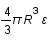 , l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
, l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
Question 5)
L'énergie gravitationnelle de l'étoile est 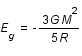 , où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon
, où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon 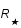 qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et
qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et 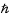 . Calculer ce rayon pour le soleil.
. Calculer ce rayon pour le soleil.
Trouver le rayon qui minimise l'énergie revient à résoudre 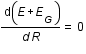 .
.
Auteur: Jérôme Thiébaut
En relativité générale la gravitation n'est pas une force mais une déformation de l'espace temps due aux corps qu'il contient. Par conséquent, la métrique, c'est à dire la manière de mesurer les distances, s'en trouve transformée par rapport aux distances euclidiennes usuelles. La métrique de Schwarzschild est une métrique applicable à un corps massif central statique ou en rotation lente. Cette métrique s'applique à l'extérieur du corps en question et n'est plus valable en son sein. Elle permet de plus, à grande distance ou dans le cas de potentiel faible, de retrouver la gravitation newtonnienne.
Le but de cet exercice est de montrer que pour des trous noirs, il existe une orbite circulaire en deça de laquelle il est impossible d'orbiter, et que cette orbite correspond à la trajectoire de photons.
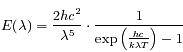
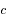 correspond à la vitesse de la lumière dans le vide,
correspond à la vitesse de la lumière dans le vide, 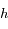 est la constante de Planck,
est la constante de Planck, 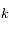 la constante de Boltzmann,
la constante de Boltzmann, 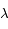 la longueur d'onde à laquelle le rayonnement est émis et
la longueur d'onde à laquelle le rayonnement est émis et 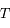 la température de surface du corps noir.
la température de surface du corps noir.
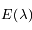 pour différentes températures de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.
pour différentes températures de surface du corps noir. On peut remarquer que le maximum de la courbe se déplace sur la gauche lorsque la température augmente. Autrement dit, la longueur d'onde pour laquelle le rayonnement émis est maximal diminue lorsque la température de surface augmente.

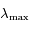 et
et 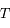 .
.
 Remarque
Remarque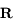 , mais ce théorème peut être admis ici.
, mais ce théorème peut être admis ici.
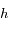 ,
, 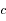 et
et 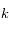 sont des constantes strictement positives et que la température
sont des constantes strictement positives et que la température 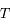 étant mesurée en Kelvin est aussi strictement positive, montrer que
étant mesurée en Kelvin est aussi strictement positive, montrer que 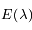 est de classe
est de classe 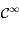 sur
sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation17.png) et est toujours strictement positive sur cet intervalle.
et est toujours strictement positive sur cet intervalle.
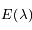 quand
quand 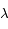 tend vers 0 et vers
tend vers 0 et vers 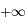 sont toutes les deux égales à zéro. Ce résultat peut être admis ici.
sont toutes les deux égales à zéro. Ce résultat peut être admis ici.
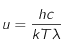 . Pour la limite en
. Pour la limite en 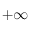 on pourra faire un dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle.
on pourra faire un dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle.
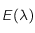 sur
sur 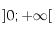 .
.
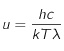 , montrer qu'étudier le signe de
, montrer qu'étudier le signe de 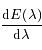
 revient à étudier celui de
revient à étudier celui de 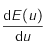 .
.
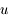 , de la forme
, de la forme 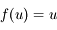 , pour que
, pour que 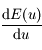 s'annule. On note
s'annule. On note 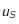 la solution de cette équation lorsqu'elle existe.
la solution de cette équation lorsqu'elle existe.
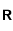 que
que 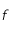 admet un point fixe et que la suite définie par
admet un point fixe et que la suite définie par 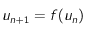 converge vers ce point fixe (voir
converge vers ce point fixe (voir 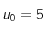 trouver une valeur
trouver une valeur 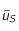 qui soit une valeur approchée de
qui soit une valeur approchée de 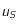 à
à 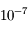 prêt.
prêt.
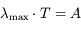 où
où 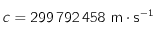 ,
, 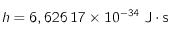 et
et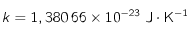 . Cette relation correspond à la loi du déplacement de Wien pour les corps noirs.
Justifier l'utilisation de
. Cette relation correspond à la loi du déplacement de Wien pour les corps noirs.
Justifier l'utilisation de 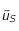 dans le calcul de la constante
dans le calcul de la constante 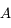 .
.
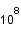 K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
K.
Le but de cet exercice est de déterminer grâce à un modèle simple le rayon d'équilibre de ces étoiles.
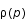 est la suivante:
est la suivante: 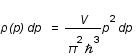 , où V est le volume et
, où V est le volume et 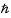 la constante de Planck réduite.
la constante de Planck réduite.
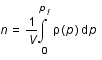 où
où 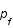 est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de
est l'impulsion de Fermi, c'est à dire l'impulsion maximale.
Exprimer n en fonction de 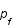 .
.
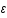 :
:
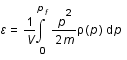 .
calculer
.
calculer 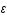 en fonction de
en fonction de 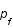 .
.
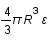 , l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
, l'exprimer en fonction de l'impulsion de Fermi puis en fonction des caractéristiques de l'étoile et de la masse du neutron.
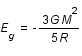 , où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon
, où G est la constante de gravitation. L'équilibre est atteint lorsque l'énergie totale (celle du gaz plus celle gravitationnelle) de l'étoile est minimum. Calculer le rayon 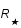 qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et
qui minimise l'énergie en fonction de la masse de l'étoile et des constantes m, G et 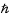 . Calculer ce rayon pour le soleil.
. Calculer ce rayon pour le soleil.
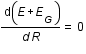 .
.
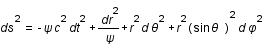 , où
, où 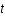 est le temps,c la vitesse de la lumière,
est le temps,c la vitesse de la lumière, 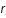
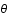
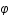 sont les coordonnées sphériques et
sont les coordonnées sphériques et 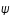 est défini comme
est défini comme 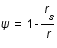 . Le rayon de Schwarzschild
. Le rayon de Schwarzschild 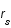 est directement relié à la masse du corps central par
est directement relié à la masse du corps central par 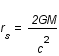 , où G est la constante de gravitation.
, où G est la constante de gravitation.
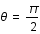 . Que vaut
. Que vaut 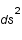 dans le cas d'une orbite circulaire ?
dans le cas d'une orbite circulaire ?
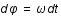 , où
, où 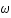 est la fréquence angulaire du mouvement vu par un observateur lointain. Sachant que pour qu'un mouvement soit physiquement réalisable il faut que
est la fréquence angulaire du mouvement vu par un observateur lointain. Sachant que pour qu'un mouvement soit physiquement réalisable il faut que 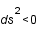 (ceci vient uniquement d'un choix spécifique de métrique); déterminer la condition sur
(ceci vient uniquement d'un choix spécifique de métrique); déterminer la condition sur 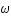 .
.
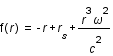
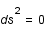 . Que vaut son rayon ?
. Que vaut son rayon ?
 s'écrit comme un produit et composition de fonction de classe
s'écrit comme un produit et composition de fonction de classe 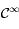 sur leur ensemble de définition. Ainsi
sur leur ensemble de définition. Ainsi 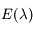 est de classe
est de classe 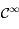 sur son intervalle de définition, c'est à dire sur
sur son intervalle de définition, c'est à dire sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation22.png) .
.
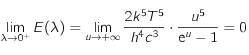 car l'exponentielle l'emporte sur tout polynôme en
car l'exponentielle l'emporte sur tout polynôme en 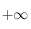 .
.
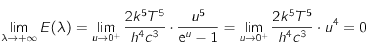 où on a utilisé le dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle :
où on a utilisé le dévelopement limité en 0 à l'ordre 1 de la fonction exponentielle :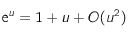 .
.
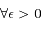 ,
, 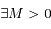 et
et 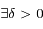 tels que
tels que 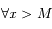 on a
on a 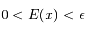 et
et 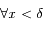 et
et 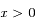 on a
on a 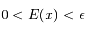 .
.
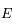 est une fonction continue sur l'intervalle
est une fonction continue sur l'intervalle ![[\delta,M]](../pages_extremas/equations_extremas/equation43.png) . Or l'image d'un segment fermé par une fonction continue est un segment fermé. Ce dernier possède donc une borne supérieure qui est atteinte par la fonction
. Or l'image d'un segment fermé par une fonction continue est un segment fermé. Ce dernier possède donc une borne supérieure qui est atteinte par la fonction 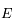 sur
sur ![[\delta,M]](../pages_extremas/equations_extremas/equation45.png) .
.
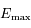 ce maximum. On peut alors choisir
ce maximum. On peut alors choisir 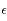 pour que
pour que 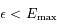 , ainsi
, ainsi 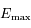 sera aussi le maximum de
sera aussi le maximum de 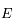 sur
sur ![]0,+\infty[](../pages_extremas/equations_extremas/equation51.png) .
.
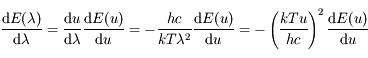 ,
,
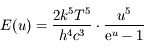 donc
donc 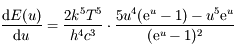 .
.
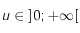 , et que
, et que 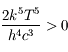 on a
on a 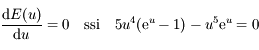 .
.
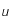 peut se mettre sous la forme
peut se mettre sous la forme 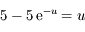 .
.
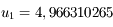
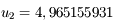
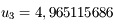
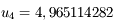
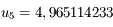
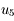 est une approximation qui répond à la question.
est une approximation qui répond à la question.
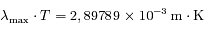 .
.
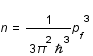
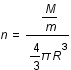
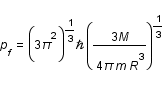
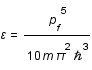
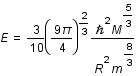
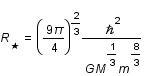 L'application numérique donne pour une étoile d'une masse solaire un rayon de 12km !
L'application numérique donne pour une étoile d'une masse solaire un rayon de 12km !
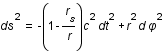
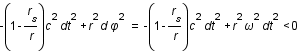
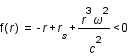
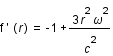
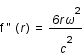 La dérivée seconde est toujours positive, la fonction est donc convexe. Son minimum est atteint en
La dérivée seconde est toujours positive, la fonction est donc convexe. Son minimum est atteint en 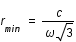 lorsque la dérivé s'annule. Lorsque
lorsque la dérivé s'annule. Lorsque 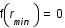 , il n'y a plus de solution possible donc
, il n'y a plus de solution possible donc 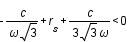 soit
soit 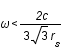
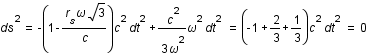
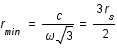 Ce rayon correspond à la dernière orbite possible pour des photons c'est la sphère photonique.
Ce rayon correspond à la dernière orbite possible pour des photons c'est la sphère photonique.