Auteur: Jérôme Thiébaut
Les équations d'Einstein de la relativité générale appliquées à l'univers que l'on suppose être un fluide homogène et isotrope, aboutissent à l'équation de Friedmann,
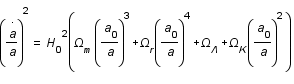 ,
,
décrivant l'évolution de l'univers en fonction de son contenu.
Ce contenu est défini par les paramètres de densité de matière, 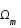 , de rayonnement,
, de rayonnement, 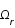 , de constante cosmologique,
, de constante cosmologique, 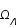 et de courbure,
et de courbure, 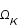 .
.
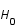 est la constante de Hubble et
est la constante de Hubble et 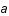 est le facteur d'échelle décrivant l'évolution de l'univers.
La composition de l'univers évoluant avec le temps, les différents paramètres de densité ont des importances relatives différentes en fonction de l'ère cosmologique considérée. Ils sont tour à tour dominants (
est le facteur d'échelle décrivant l'évolution de l'univers.
La composition de l'univers évoluant avec le temps, les différents paramètres de densité ont des importances relatives différentes en fonction de l'ère cosmologique considérée. Ils sont tour à tour dominants (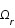 puis
puis 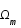 et
et 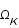 et enfin
et enfin 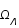 ) ou négligeables.
On se propose dans cet exercice d'étudier un modèle d'univers dominé par la matière avec une courbure négative et de vérifier si il peut coïncider avec les observations actuelles.
) ou négligeables.
On se propose dans cet exercice d'étudier un modèle d'univers dominé par la matière avec une courbure négative et de vérifier si il peut coïncider avec les observations actuelles.
Auteur: Jérôme Thiébaut
 Univers à courbure négative
Univers à courbure négative
Difficulté : ☆☆
Temps : 30 mn
On considère un univers dominé par la matière non relativiste et avec une courbure négative. Dans ce cas, l'équation de Friedmann s'écrit:
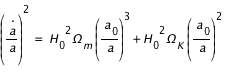
où 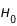 est la constante de Hubble,
est la constante de Hubble, 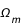 le paramètre de densité et
le paramètre de densité et 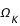 le paramètre de courbure.
La solution sous une forme paramétrique est:
le paramètre de courbure.
La solution sous une forme paramétrique est:
 ,
,  ,
où
,
où 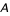 et
et 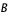 sont des constantes.
sont des constantes.
Question 2)
Calculer les constantes 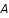 et
et 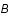 comme fonction de la constante de Hubble et des paramètres de densité et de courbure.
comme fonction de la constante de Hubble et des paramètres de densité et de courbure.
Réduire au même dénominateur et identifier les puissances de 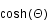 .
.
Question 3)
Calculer le paramètre de décélération 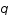 défini comme:
défini comme: 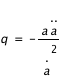 .
Les observations actuelles montrent que l'univers est dans une phase d'accélération. Ce type d'univers a t'il une phase accélérée ? Peut-il représenter notre univers ?
.
Les observations actuelles montrent que l'univers est dans une phase d'accélération. Ce type d'univers a t'il une phase accélérée ? Peut-il représenter notre univers ?
Auteur : Marc Fouchard.
Le but de cet exercice est de résoudre l'équation de Kepler dans le cas hyperbolique. On a déjà vu ici comment résoudre l'équation de Kepler dans le cas elliptique. On va voir ci une méthode similaire pour une trajectoire hyperbolique. Dans ce cas l'équation de Kepler est :
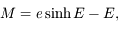
où 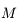 est l'anomalie moyenne,
est l'anomalie moyenne, 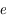 est l'excentricité (qui est
est l'excentricité (qui est 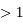 dans le cas hyperbolique) et
dans le cas hyperbolique) et 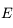 est l'anomalie excentrique. On peut voir ici une animation avec le lien entre les trois anomalies dans le cas hyperbolique. (
est l'anomalie excentrique. On peut voir ici une animation avec le lien entre les trois anomalies dans le cas hyperbolique. (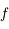 correspond à l'anomalie vraie)
correspond à l'anomalie vraie)
Auteur: Marc Fouchard
 équation de Kepler hyperbolique
équation de Kepler hyperbolique
Difficulté : ☆☆
Temps : 1h
Question 3)
Montrer que la courbe représentative de 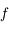 est au-dessus de sa tangente sur
est au-dessus de sa tangente sur 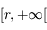 .
.
Question 4)
En déduire que la suite 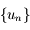 définie par:
définie par:
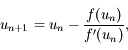
avec 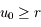 , est décroissante et minorée par
, est décroissante et minorée par 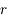 .
.
Question 5)
En déduire que la suite 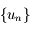 converge et que sa limite est
converge et que sa limite est 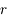 .
.
Cette propriété de la suite 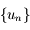 est utilisée pour résoudre par itération et de manière approchée l'équation de Kepler.
est utilisée pour résoudre par itération et de manière approchée l'équation de Kepler.
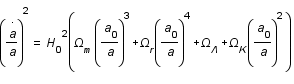 ,
,
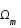 , de rayonnement,
, de rayonnement, 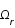 , de constante cosmologique,
, de constante cosmologique, 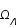 et de courbure,
et de courbure, 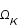 .
.
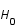 est la constante de Hubble et
est la constante de Hubble et 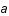 est le facteur d'échelle décrivant l'évolution de l'univers.
La composition de l'univers évoluant avec le temps, les différents paramètres de densité ont des importances relatives différentes en fonction de l'ère cosmologique considérée. Ils sont tour à tour dominants (
est le facteur d'échelle décrivant l'évolution de l'univers.
La composition de l'univers évoluant avec le temps, les différents paramètres de densité ont des importances relatives différentes en fonction de l'ère cosmologique considérée. Ils sont tour à tour dominants (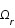 puis
puis 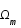 et
et 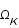 et enfin
et enfin 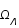 ) ou négligeables.
On se propose dans cet exercice d'étudier un modèle d'univers dominé par la matière avec une courbure négative et de vérifier si il peut coïncider avec les observations actuelles.
) ou négligeables.
On se propose dans cet exercice d'étudier un modèle d'univers dominé par la matière avec une courbure négative et de vérifier si il peut coïncider avec les observations actuelles.
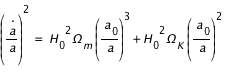
 est la constante de Hubble,
est la constante de Hubble,  le paramètre de densité et
le paramètre de densité et  le paramètre de courbure.
La solution sous une forme paramétrique est:
le paramètre de courbure.
La solution sous une forme paramétrique est:
 ,
,  ,
où
,
où 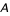 et
et 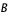 sont des constantes.
sont des constantes.
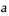 et
et 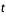 par rapport au temps et éliminer la dépendance en
par rapport au temps et éliminer la dépendance en 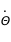 de
de 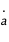 .
.
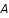 et
et 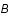 comme fonction de la constante de Hubble et des paramètres de densité et de courbure.
comme fonction de la constante de Hubble et des paramètres de densité et de courbure.
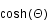 .
.
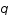 défini comme:
défini comme: 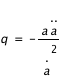 .
Les observations actuelles montrent que l'univers est dans une phase d'accélération. Ce type d'univers a t'il une phase accélérée ? Peut-il représenter notre univers ?
.
Les observations actuelles montrent que l'univers est dans une phase d'accélération. Ce type d'univers a t'il une phase accélérée ? Peut-il représenter notre univers ?
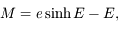
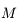 est l'
est l'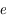 est l'
est l'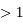 dans le cas hyperbolique) et
dans le cas hyperbolique) et 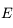 est l'
est l'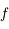 correspond à l'
correspond à l'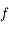 la fonction définie par
la fonction définie par 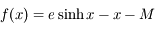 sur
sur 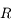 avec
avec 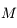 une constante. Montrer que
une constante. Montrer que 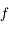 est continue dérivable 2 fois, que
est continue dérivable 2 fois, que 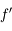 est strictement supérieure à zéro et que
est strictement supérieure à zéro et que 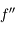 est supérieure à zéro pour
est supérieure à zéro pour 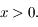 On rappelle que dans le cas hyperbolique
On rappelle que dans le cas hyperbolique 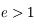 .
.
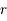 , le nombre réel positif tel que
, le nombre réel positif tel que 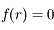 . Montrer que pour
. Montrer que pour 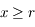 ,
, 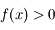 .
.
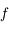 est au-dessus de sa tangente sur
est au-dessus de sa tangente sur 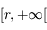 .
.
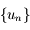 définie par:
définie par:
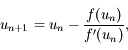
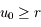 , est décroissante et minorée par
, est décroissante et minorée par 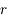 .
.
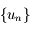 converge et que sa limite est
converge et que sa limite est 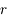 .
.
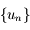 est utilisée pour résoudre par itération et de manière approchée l'équation de Kepler.
est utilisée pour résoudre par itération et de manière approchée l'équation de Kepler.
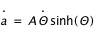 ,
,
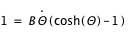 ,
,
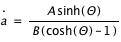
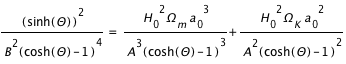 ,
,
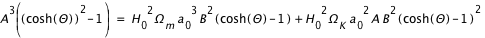 .
.
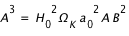 et
et
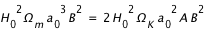 .
.
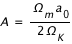 et
et 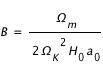 .
.
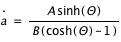
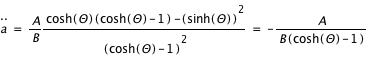
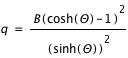 Le paramètre de décélération étant toujours positif, ce type d'univers n'a pas de phase d'accélération. Il n'est donc pas compatible avec le nôtre puisque nous sommes dans une phase d'expansion accélérée.
Le paramètre de décélération étant toujours positif, ce type d'univers n'a pas de phase d'accélération. Il n'est donc pas compatible avec le nôtre puisque nous sommes dans une phase d'expansion accélérée.
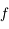 est continue, dérivable deux fois sur
est continue, dérivable deux fois sur 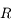 .
.
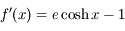 . Pour tout
. Pour tout 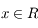 ,
, 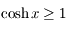 . Comme
. Comme 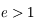 on en déduit que
on en déduit que 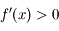 pour
pour 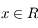 .
.
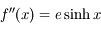 . Pour
. Pour 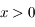 on a donc bien
on a donc bien 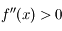 .
.
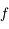 est strictement croissante sur
est strictement croissante sur  . Comme
. Comme 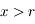 et que
et que 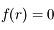 on a bien
on a bien 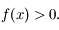
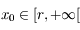 , on a:
, on a:
![g(x)=f(x)-[f(x_0)+f'(x_0)(x-x_0)]](../pages_hyper/equations_hyper/equation79.png) .
.
 et
et 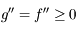 . Ainsi
. Ainsi 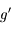 est une fonction croissante au voisinage de
est une fonction croissante au voisinage de 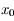 , donc
, donc 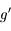 est négative pour
est négative pour 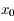 et positive pour
et positive pour 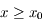 . Donc
. Donc 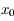 correspond à un minimum pour
correspond à un minimum pour 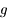 . Ainsi au voisinage de
. Ainsi au voisinage de 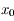 on a
on a 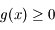 ce qui montre que la courbe représentative de
ce qui montre que la courbe représentative de 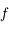 est effectivement au-dessus de sa tangente.
est effectivement au-dessus de sa tangente.
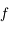 et
et 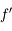 sont positives sur
sont positives sur 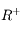 , la suite
, la suite 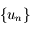 est effectivement décroissante tant que les valeurs de la suite restent dans
est effectivement décroissante tant que les valeurs de la suite restent dans 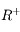 .
D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse
.
D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse 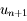 est le point d'intersection de la tangente au point d'abscisse
est le point d'intersection de la tangente au point d'abscisse 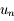 à la courbe représentative de
à la courbe représentative de 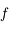 avec l'axe des abscisses, on en déduit que
avec l'axe des abscisses, on en déduit que 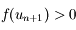 puisque la tangente est en-dessous de la courbe représentative de
puisque la tangente est en-dessous de la courbe représentative de 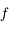 . Comme
. Comme 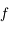 est croissante et que
est croissante et que 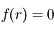 on a bien
on a bien 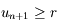 .
.
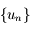 étant décroissante et minorée par
étant décroissante et minorée par 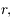 elle converge vers une limite
elle converge vers une limite 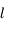 . A la limite on a :
. A la limite on a :
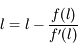 ,
,
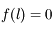 . Ainsi on a bien
. Ainsi on a bien 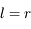 .
.