Equation de Kepler elliptique

Auteur: Marc Fouchard

Lien entre les 3 anomalies

Crédit : Astrophysique sur Mesure / Bessou Fouchard

Marc Fouchard

Le but de cet exercice est de résoudre l'équation de Kepler par la méthode de Newton.

L'équation de Kepler est:

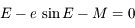
$E-e\,\sin E -M =0$

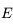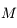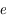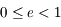où s'appelle l'anomalie excentrique, l'anomalie moyenne et l'excentricité. Dans le cas présent on a $0\le e < 1$ , $M\in [0;2\pi]$ et $E\in[0;2\pi]$ . Dans l'exercice on va se limiter à l'intervalle $[0;\pi]$ . On peut facilement en déduire la résolution de l'équation dans l'intervalle $[\pi;2\pi]$ par symétrie. La figure ci-dessus montre le lien entre ces anomalies.

On peut voir l'exercice suivant pour voir des méthodes plus complexes de résolution de l'équation de Kepler. Le cas hyperbolique fait l'objet de cet exercice.