Equation de Kepler

Auteur : Marc Fouchard

Dans le problème de deux corps (voir cet exercice), on sait que le déplacement d'un corps par rapport à l'autre se fait sur une conique dont le deuxième corps occupe l'un des foyers (voir aussi cet . Une fois la conique fixée il ne reste alors qu'à positionner le corps sur son orbite. Pour cela on utilise une quantité qu'on appelle anomalie. On définie trois types d'anomalie: l'anomalie moyenne, l'anomalie vraie et l'anomalie excentrique.

Les trois anomalies

Crédit : Astrophysique sur Mesure / Bessou Fouchard

L'animation ci-dessus montre le lien entre les 3 anomalies. Comme on peut le voir, l'anomalie moyenne correspond en fait à un temps. Il n'existe pas de relation géométrique entre l'anomalie moyenne et les autres anomalies. En revanche, il existe une relation (voir cet exercice), appelée équation de Kepler, qui relie l'anomalie moyenne à l'anomalie excentrique. Cette relation est:

,

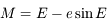où 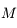est l'anomalie moyenne, 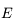l'anomalie excentrique et 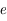l'excentricité de la trajectoire.

On voit que connaissant 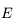il est facile d'avoir 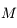, mais en revanche connaissant 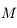il n'est pas possible d'avoir 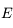sous forme analytique. L'objet de cette exercice est justement de déterminer un algorithme puissant d'inversion de cette équation.