Auteur: Marc Fouchard

 Générateur de coefficients de Taylor
Générateur de coefficients de Taylor
Difficulté : ☆☆
Temps : 30mn
Question 2)
Déterminer 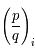 .
.
Solution
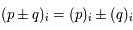
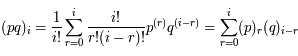
Soit 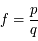 . Ainsi on a
. Ainsi on a 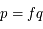 . D'après le résultat précédent on en déduit que
. D'après le résultat précédent on en déduit que 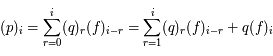 .
.
Ainsi :
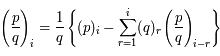
Question 3)
Montrer que :
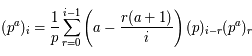
AideSolution
On pourra développer de deux manière différentes 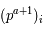
On a 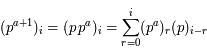 .
.
De même, on a:
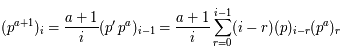
En identifant les deux expressions et en isolant le terme avec 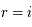 dans la première somme on trouve bien le résultat demandé.
dans la première somme on trouve bien le résultat demandé.

