Ex: Limites de la loi de Planck

Auteurs: Marc Fouchard, Jérôme Thiébaut, S. Renner, Stéphane Erard

Auteur: Stéphane Erard

Limites de la loi de Plack

Difficulté : ☆ Temps : 30 min

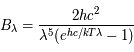
On connaît la luminance du corps noir en fonction de la longueur d'onde, donnée par la loi de Planck (voir par exemple l'exercice sur la loi de Wien) : $B_{\lambda} = \frac{2hc^2}{\lambda^5 (e^{hc/kT\lambda} -1) }$

où 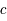est la vitesse de la lumière dans le vide, 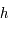la constante de Planck, 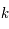la constante de Boltzmann, 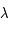$\lambda$ la longueur d'onde et 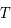la température du corps noir.

Cette expression donne la luminance directionnelle, en 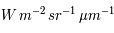$W\,m^{-2}\,sr^{-1}\,\mu m^{-1}$ , du corps noir à toutes les longueurs d'onde.

Question 1)

Donner une expression de cette loi à courtes longueurs d'onde. Cette expression est connue sous le nom de loi ou distribution de Wien.

Solution

Question 2)

Donner une expression de cette loi à grandes longueurs d'onde. Cette expression est connue sous le nom de loi de Rayleigh-Jeans. Commentaire ?

Solution

Question 3)

Tracer les graphiques de ces deux expressions et de la loi de Planck en échelle log/log, comparer. Quel problème pose l'approximation de Rayleigh-Jeans ?

Solution