 |  |  |  |  |  |
Développements d'une fonction d'une variable réelle
Ex: Effet de marée et limite de Roche |
Effet de marée et limite de RocheDifficulté : ☆☆ Temps : 1h
On se place dans un référentiel galiléen centré sur la planète, supposée sphérique, homogène, de masse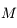 
, rayon 
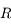, et masse volumique 
.
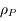On suppose que le satellite est constitué de deux sphères homogènes identiques (de masse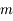 
, de rayon 
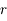et de masse volumique 
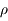), et qu'il est en orbite circulaire de rayon 
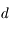autour de la planète.
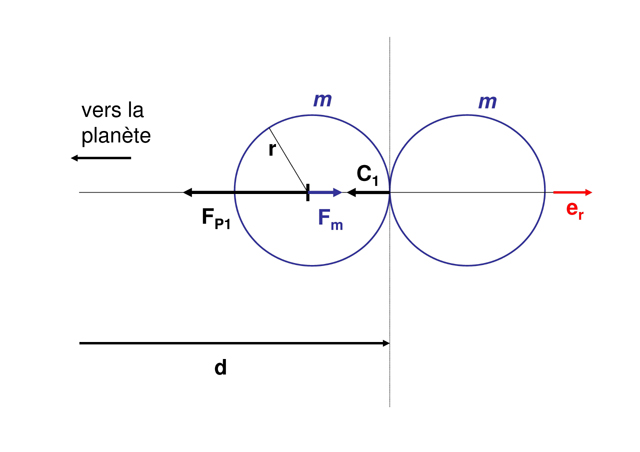
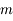dans le repère lié à la planète (supposé galiléen) : 
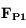est la force d'attraction gravitationnelle de la planète, 
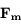celle de la deuxième sphère de masse 
, 
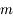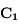la force de contact entre les deux sphères.
En appliquant le principe fondamental de la dynamique (PFD) au système des deux masses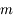 
, montrer qu'au premier ordre en 
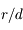la vitesse
angulaire de la comète est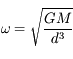 
.
Appliquer le PFD à l'une des masses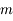 
, et trouver un critère de fragmentation du satellite (contact rompu entre les deux sphères) au premier ordre en 
.
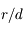En déduire l'expression de la limite de Roche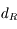 
en fonction de 
, 
, 
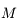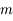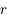, puis en fonction de 
, 
, 
.
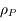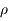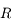Retrouver l'expression de la limite de Roche en écrivant que la différence de force entre les deux masses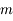 
due à l'attraction gravitationnelle de la planète est supérieure à la force de gravitation mutuelle entre les deux sphères.
 |  |
: 
(les caractères en gras désignent des vecteurs)
, 
,
est un vecteur unitaire radial. On obtient alors :
, 
et 
au premier ordre en 
. On retrouve la troisième loi de Kepler.
, avec 
et 
.
, i.e. lorsque 
.
et 
, on obtient :
![d_R=R \sqrt[\displaystyle 3]{12 \frac{\rho_P}{\rho}} \simeq 2.29 R \sqrt[\displaystyle 3]{ \frac{\rho_P}{\rho}}](../pages_dl/equations_dl/equation205.png)
.
.
![\Delta F \geq F_m \Longleftrightarrow d \leq R \sqrt[\displaystyle 3]{16 \frac{\rho_P}{\rho}} \simeq 2.52 R \sqrt[\displaystyle 3]{\frac{\rho_P}{\rho}}](../pages_dl/equations_dl/equation209.png)
.