Ex: Equation de Kepler

Auteurs: Marc Fouchard, Jérôme Thiébaut, S. Renner, Stéphane Erard

Auteur: Marc Fouchard

Equation de Kepler

Difficulté : ☆☆ Temps : 1h30

Question 1)

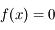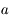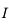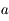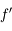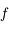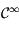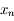On souhaite résoudre une équation du type f(x)=0 . Soit une solution à l'équation. On supposera dans la suite que, sur un intervalle contenant , ne s'annulle jamais et que est de classe $\mathcal{C}^{\infty}$ sur cet intervalle. Soit x_n , la suite définie par :

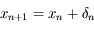$x_{n+1}=x_n+\delta_n$ ,

avec 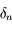$\delta_n$ , la solution de 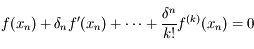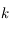$f(x_n)+\delta_n f'(x_n)+\cdots+\frac{\delta^n}{k!}f^{(k)}(x_n)=0$ ( étant fixé).

On souhaite montrer que si la suite 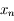x_n converge vers 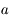, alors elle converge au moins avec l'ordre k+1 .

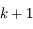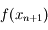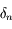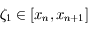Calculer $f(x_{n+1})$ en fonction de $\delta_n$ et un nombre $\zeta_1 \in \lbrack x_n,x_{n+1}\rbrack$ .

Solution

Question 2)

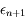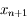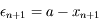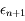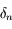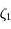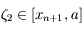Soit $\epsilon_{n+1}$ l'erreur de $x_{n+1}$ définie par $\epsilon_{n+1}=a-x_{n+1}$ . Cacluler $\epsilon_{n+1}$ en fonction de $\delta_n$ , $\zeta_1$ et un nombre $\zeta_2 \in \lbrack x_{n+1},a\rbrack$ .

Solution

Question 3)

Montrer que:

$\frac{\epsilon_n}{\delta_n}=\frac{f'(x_n)}{f'(\zeta_3)}+\frac{\delta_n}{2!}\frac{f''(x_n)}{f'(\zeta_3)}+\cdots+\frac{\delta_n^{k-1}}{k!}\frac{f^{(k)}(x_n)}{f'(\zeta_3)}$ , avec $\zeta_3$ un nombre entre et x_n .

Solution

Question 4)

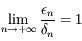En déduire que $\lim_{n\to +\infty}\frac{\epsilon_n}{\delta_n}=1$ .

Solution

Question 5)

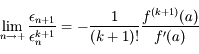En déduire que $\lim_{n\to+\inty}\frac{\epsilon_{n+1}}{\epsilon_n^{k+1}}=-\frac{1}{(k+1)!}\frac{f^{(k+1)}(a)}{f'(a)}$ , et que la suite 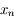x_n converge vers 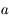au moins à l'ordre k+1 .

Solution

Question 6)

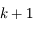Il nous faut maintenant calculer la solution 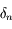$\delta_n$ de l'équation qui le défini. Avant tout, jusitfier pourquoi il suffit d'avoir une solution approxée à 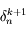$\delta_n^{k+1}$ près.

Solution

Question 7)

Montrer que pour k=3 , on a:

$\delta_n=-\frac{f(x_n)}{f'(x_n)+\frac{1}{2}\delta_n f''(x_n)+\frac{1}{6}\delta_n^2f'''(x_n)}$

Solution

Question 8)

Montrer qu'en utilisant la séquance suivante:

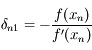$\delta_{n1}=-\frac{f(x_n)}{f'(x_n)}$ ,

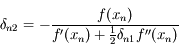$\delta_{n2}=-\frac{f(x_n)}{f'(x_n)+\frac{1}{2}\delta_{n1}f''(x_n)}$ ,

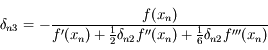$\delta_{n3}=-\frac{f(x_n)}{f'(x_n)+\frac{1}{2}\delta_{n2}f''(x_n)+\frac{1}{6}\delta_{n2}f'''(x_n)}$ ,

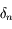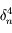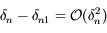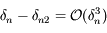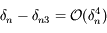on obtient une approximation de $\delta_n$ à $\delta_n^4$ près. On pourra procéder par étape en montrant que $\delta_n-\delta_{n1}=\mathcal{O}(\delta_n^2)$ , puis que $\delta_n-\delta_{n2}=\mathcal{O}(\delta_n^3)$ et enfin que $\delta_n-\delta_{n3}=\mathcal{O}(\delta_n^4)$ .

Solution

Question 9)

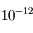Montrer que l'on peut appliquer l'algorithme précédent pour inverser l'équation de Kepler sur l'intervalle $[0,2\pi]$ . Aplliquer l'algorithme à quelque exemple et remarquer qu'on obtient une erreur inférieure à $10^{-12}$ en moins de 4 itérations.

Solution