

Ex : Lentille gravitationnelle |
Difficulté : ☆ Temps : 30 min
La figure montre le schéma du principe d'une lentille gravitationnelle. La source, S, est déviée par la lentille, L, et son image, I, est donc vue par l'observateur, O, selon un angle 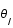 au lieu de
au lieu de 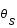 .
.
Exprimer les distances AS et AI en fonction des angles 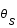 et
et 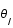 et de la distance OS.
et de la distance OS.
Les calculs relativistes montrent que la distance SI vaut 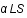 où l'angle de déviation,
où l'angle de déviation, 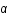 , vaut
, vaut 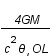 , avec G la constante de gravitation, M la masse de la lentille et c la vitesse de la lumière.
Dans l'approximation des petits angles, déterminer l'équation du second degré à laquelle obéit
, avec G la constante de gravitation, M la masse de la lentille et c la vitesse de la lumière.
Dans l'approximation des petits angles, déterminer l'équation du second degré à laquelle obéit 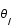 en fonction de
en fonction de 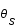 , et des grandeurs caractéristiques du système, LS, OS, OL et M.
, et des grandeurs caractéristiques du système, LS, OS, OL et M.