Marc Fouchard
Le but de cet exercice est de résoudre l'équation de Kepler par la méthode de Newton.
L'équation de Kepler est:
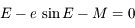
où 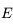 s'appelle l'anomalie excentrique,
s'appelle l'anomalie excentrique, 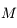 l'anomalie moyenne et
l'anomalie moyenne et 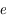 l'excentricité. Dans le cas présent on a
l'excentricité. Dans le cas présent on a 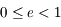 ,
, ![M\in [0;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation6.png) et
et ![E\in[0;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation7.png) .
Dans l'exercice on va se limiter à l'intervalle
.
Dans l'exercice on va se limiter à l'intervalle ![[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation8.png) . On peut facilement en déduire la résolution de l'équation dans l'intervalle
. On peut facilement en déduire la résolution de l'équation dans l'intervalle ![[\pi;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation9.png) par symétrie.
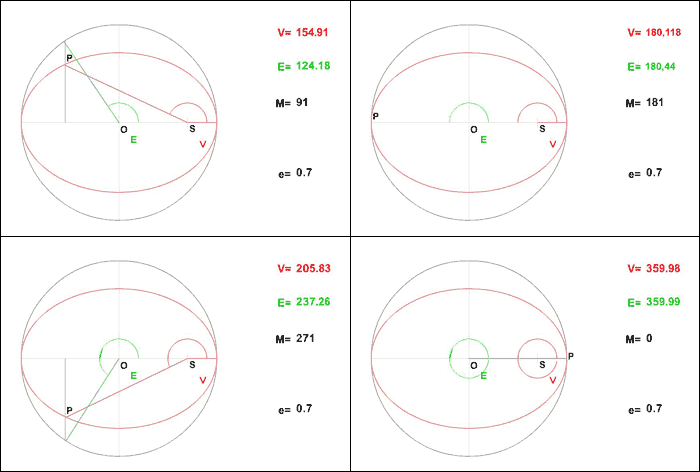
La figure ci-dessus montre le lien entre ces anomalies.
par symétrie.
La figure ci-dessus montre le lien entre ces anomalies.
Lien entre les 3 anomalies
On peut voir l'exercice suivant pour voir des méthodes plus complexes de résolution de l'équation de Kepler. Le cas hyperbolique fait l'objet de cet exercice.
Auteur: Marc Fouchard
 équation de Kepler elliptique
équation de Kepler elliptique
Difficulté : ☆
Temps : 30 mn
Question 3)
Montrer que la courbe représentative de 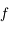 est au dessus de sa tangente sur
est au dessus de sa tangente sur ![[r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation39.png) .
.
Question 4)
En déduire que la suite 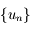 définie par:
définie par:
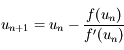 ,
,
avec 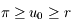 , est décroissante et minorée par
, est décroissante et minorée par 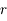 .
.
Question 5)
En déduire que la suite 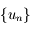 converge et que sa limite est
converge et que sa limite est 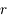 .
.
-
Question 1
Solution :
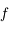 est évidemment continue est dérivable deux fois puisqu'elle est la somme d'une fonction affine et de la fonction sinus.
On a:
est évidemment continue est dérivable deux fois puisqu'elle est la somme d'une fonction affine et de la fonction sinus.
On a:
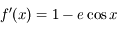 .
.
Comme 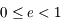 , on a bien
, on a bien 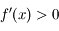 pour tout
pour tout  de
de  .
.
De même on a:
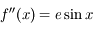 ,
,
donc on a bien 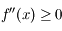 pour tout
pour tout ![x\in[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation25.png) .
.
-
Question 2
Solution :
Sur ![[r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation32.png) ,
, 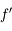 est strictement positive, donc
est strictement positive, donc 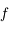 est strictement croissante. Comme
est strictement croissante. Comme 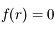 on en déduit que
on en déduit que 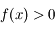 sur
sur ![]r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation37.png) .
.
-
Question 3
Solution :
En ![x_0\in[r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation40.png) on a:
on a:
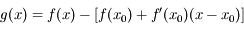 .
.
On remarque facilement que 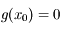 ,
, 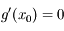 et
et 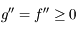 . Ainsi
. Ainsi 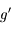 est une fonction croissante au voisinage de
est une fonction croissante au voisinage de 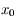 , donc
, donc 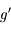 est négative pour
est négative pour 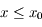 et positive pour
et positive pour 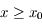 . Donc
. Donc 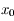 correspond à une minimum pour
correspond à une minimum pour 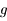 . Ainsi au voisinage de
. Ainsi au voisinage de 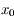 on a
on a 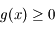 ce qui montre que la courbe représentative de
ce qui montre que la courbe représentative de 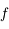 est effectivement au dessus de sa tangente.
est effectivement au dessus de sa tangente.
-
Question 4
Solution :
Comme 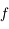 et
et 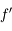 sont positives sur
sont positives sur ![[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation61.png) , la suite
, la suite 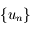 est effectivement décroissante tant que les valeurs de la suite restent dans l'intervalle
est effectivement décroissante tant que les valeurs de la suite restent dans l'intervalle ![[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation63.png) . D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse
. D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse 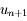 est l'intersection de la tangente au point d'abscisse
est l'intersection de la tangente au point d'abscisse 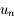 à la courbe représentative de
à la courbe représentative de 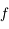 avec l'axe des abscisses, on en déduit que
avec l'axe des abscisses, on en déduit que 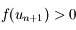 puisque la tangente est en-dessous de la courbe représentative de
puisque la tangente est en-dessous de la courbe représentative de 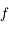 . Comme
. Comme 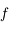 est croissante et que
est croissante et que 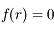 on a bien
on a bien 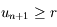 .
.
-
Question 5
Solution :
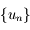 étant décroissante est minorée par
étant décroissante est minorée par 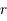 , elle converge vers une limite
, elle converge vers une limite 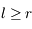 . A la limite on a :
. A la limite on a :
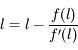 ,
,
Donc 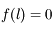 . Ainsi on a bien
. Ainsi on a bien 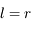 .
.
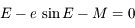
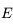 s'appelle l'anomalie excentrique,
s'appelle l'anomalie excentrique, 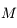 l'anomalie moyenne et
l'anomalie moyenne et 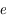 l'excentricité. Dans le cas présent on a
l'excentricité. Dans le cas présent on a 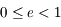 ,
, ![M\in [0;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation6.png) et
et ![E\in[0;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation7.png) .
Dans l'exercice on va se limiter à l'intervalle
.
Dans l'exercice on va se limiter à l'intervalle ![[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation8.png) . On peut facilement en déduire la résolution de l'équation dans l'intervalle
. On peut facilement en déduire la résolution de l'équation dans l'intervalle ![[\pi;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation9.png) par symétrie.
La figure ci-dessus montre le lien entre ces anomalies.
par symétrie.
La figure ci-dessus montre le lien entre ces anomalies.

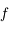 la fonction définie par
la fonction définie par 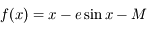 , avec
, avec ![M \in [0;2\pi]](../pages_suites-reelles/equations_suites-reelles/equation12.png) une constante.
Montrer que
une constante.
Montrer que 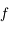 est continue, dérivable deux fois et que
est continue, dérivable deux fois et que 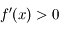 et pour
et pour ![x\in [0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation15.png) ,
, 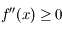 .
.
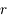 le nombre réel tel que
le nombre réel tel que 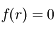 (on peut montrer rapidement que
(on peut montrer rapidement que 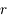 existe d'après la continuité de
existe d'après la continuité de 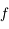 et le théorème de la valeur intermédiaire). Montrer que pour
et le théorème de la valeur intermédiaire). Montrer que pour ![x\in]r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation30.png) ,
, 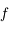 est strictement positive.
est strictement positive.
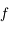 est au dessus de sa tangente sur
est au dessus de sa tangente sur ![[r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation39.png) .
.
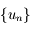 définie par:
définie par:
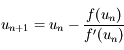 ,
,
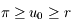 , est décroissante et minorée par
, est décroissante et minorée par 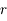 .
.
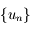 converge et que sa limite est
converge et que sa limite est 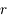 .
.
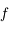 est évidemment continue est dérivable deux fois puisqu'elle est la somme d'une fonction affine et de la fonction sinus.
On a:
est évidemment continue est dérivable deux fois puisqu'elle est la somme d'une fonction affine et de la fonction sinus.
On a:
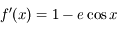 .
.
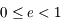 , on a bien
, on a bien 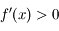 pour tout
pour tout 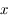 de
de 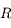 .
.
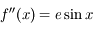 ,
,
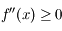 pour tout
pour tout ![x\in[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation25.png) .
.
![[r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation32.png) ,
, 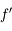 est strictement positive, donc
est strictement positive, donc 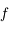 est strictement croissante. Comme
est strictement croissante. Comme 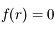 on en déduit que
on en déduit que 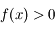 sur
sur ![]r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation37.png) .
.
![x_0\in[r;\pi]](../pages_suites-reelles/equations_suites-reelles/equation40.png) on a:
on a:
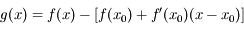 .
.
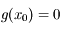 ,
, 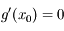 et
et 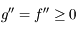 . Ainsi
. Ainsi 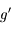 est une fonction croissante au voisinage de
est une fonction croissante au voisinage de 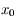 , donc
, donc 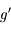 est négative pour
est négative pour 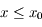 et positive pour
et positive pour 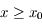 . Donc
. Donc 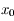 correspond à une minimum pour
correspond à une minimum pour 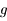 . Ainsi au voisinage de
. Ainsi au voisinage de 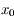 on a
on a 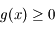 ce qui montre que la courbe représentative de
ce qui montre que la courbe représentative de 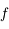 est effectivement au dessus de sa tangente.
est effectivement au dessus de sa tangente.
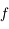 et
et 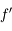 sont positives sur
sont positives sur ![[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation61.png) , la suite
, la suite 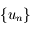 est effectivement décroissante tant que les valeurs de la suite restent dans l'intervalle
est effectivement décroissante tant que les valeurs de la suite restent dans l'intervalle ![[0;\pi]](../pages_suites-reelles/equations_suites-reelles/equation63.png) . D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse
. D'autre part, en remarquant que le point de l'axe des abscisses d'abscisse 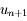 est l'intersection de la tangente au point d'abscisse
est l'intersection de la tangente au point d'abscisse 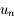 à la courbe représentative de
à la courbe représentative de 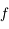 avec l'axe des abscisses, on en déduit que
avec l'axe des abscisses, on en déduit que 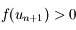 puisque la tangente est en-dessous de la courbe représentative de
puisque la tangente est en-dessous de la courbe représentative de 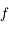 . Comme
. Comme 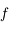 est croissante et que
est croissante et que 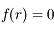 on a bien
on a bien 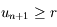 .
.
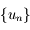 étant décroissante est minorée par
étant décroissante est minorée par 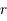 , elle converge vers une limite
, elle converge vers une limite 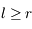 . A la limite on a :
. A la limite on a :
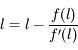 ,
,
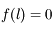 . Ainsi on a bien
. Ainsi on a bien 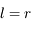 .
.